NHK_The_Cosmic_Code_Breakers.html
[NHK] The Cosmic Code Breakers
https://www.youtube.com/watch?v=eSOlPnnXnXA
==================================================
All numbers can be represented by multiplication of prime numbers
For example,
$$$255=5\times 51$$$
$$$255=5\times (3\times 17)$$$
5, 3, 17 can't be divided further
So, numbers which can't be divided further are "prime numbers"
==================================================
Prime numbers don't look showing up regularly
For example,
They show up quite in a row at some part
 But they don't show up for a while at some part
But they don't show up for a while at some part
 ==================================================
Riemann hypothesis:
Non-trivial zero points of Zeta function will be on one line
==================================================
Following equation
which shows relationship between prime number and pi
was created by Euler
$$$\dfrac{2^2}{2^2-1} \times
\dfrac{3^2}{3^2-1} \times
\dfrac{5^2}{5^2-1} \times
\dfrac{7^2}{7^2-1} \times
\dfrac{11^2}{11^2-1} \times
... =\dfrac{\pi^2}{6}$$$
==================================================
Zeta function of Riemann
$$$\zeta(x) = \prod\limits_p \dfrac{p^x}{p^x-1}
= \dfrac{2^x}{2^x-1} \times
\dfrac{3^x}{3^x-1} \times
\dfrac{5^x}{5^x-1} \times
\dfrac{7^x}{7^x-1} \times
\dfrac{11^x}{11^x-1} \times
...$$$
==================================================
==================================================
Riemann hypothesis:
Non-trivial zero points of Zeta function will be on one line
==================================================
Following equation
which shows relationship between prime number and pi
was created by Euler
$$$\dfrac{2^2}{2^2-1} \times
\dfrac{3^2}{3^2-1} \times
\dfrac{5^2}{5^2-1} \times
\dfrac{7^2}{7^2-1} \times
\dfrac{11^2}{11^2-1} \times
... =\dfrac{\pi^2}{6}$$$
==================================================
Zeta function of Riemann
$$$\zeta(x) = \prod\limits_p \dfrac{p^x}{p^x-1}
= \dfrac{2^x}{2^x-1} \times
\dfrac{3^x}{3^x-1} \times
\dfrac{5^x}{5^x-1} \times
\dfrac{7^x}{7^x-1} \times
\dfrac{11^x}{11^x-1} \times
...$$$
==================================================
 Graph of Zeta function
==================================================
Graph of Zeta function
==================================================

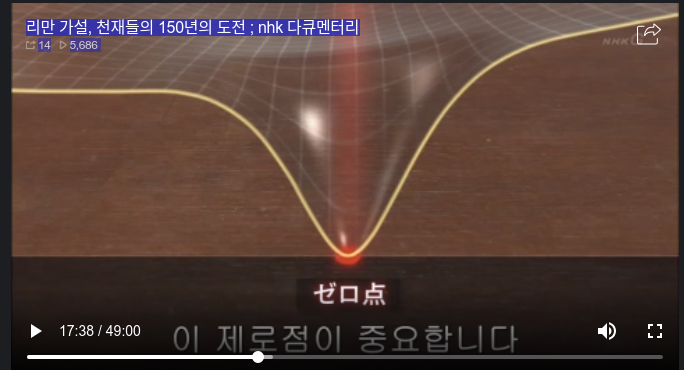 Above shows location of point (called zero point)
which has zero height in the graph
==================================================
Above shows location of point (called zero point)
which has zero height in the graph
==================================================
 Where zero point will show?
==================================================
Riemann found 4 zero points
Where zero point will show?
==================================================
Riemann found 4 zero points
 And found zero points were on the one line like following
And found zero points were on the one line like following
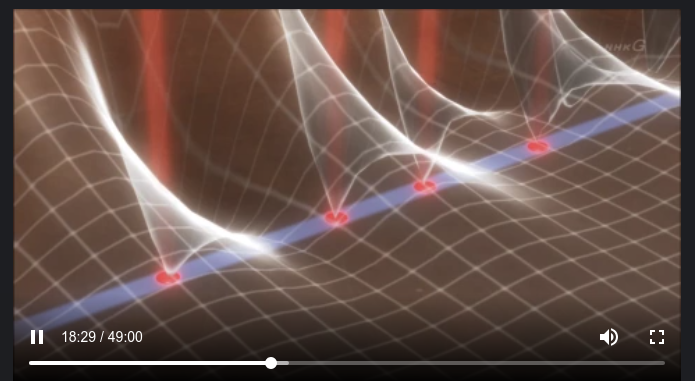 ==================================================
It's amazing because even if prime numbers show up in non-regular form,
but zero points which are derived from zeta function
and are more originally derived from prime numbers
show up in regular form.
==================================================
But since Riemann only found 4 zero points,
he needed to think how about last all zero points?
Would it be also on the one line like this?
==================================================
It's amazing because even if prime numbers show up in non-regular form,
but zero points which are derived from zeta function
and are more originally derived from prime numbers
show up in regular form.
==================================================
But since Riemann only found 4 zero points,
he needed to think how about last all zero points?
Would it be also on the one line like this?
 ==================================================
Hypothesis of "Would it be also on the one line like this?"
is that non-trivial zero points of Zeta function will be on one line
==================================================
If above hypothesis is proved,
it means that arrange of prime numbers has some regular rule
in mathematical aspect
==================================================
So, in conclusion,
problem of finding rule in prime numbers
is converted into problem of proving hypothesis
saying all zero points are on the one line?
==================================================
Hardy had proved that infinite zero points would be on the one line like this
==================================================
Hypothesis of "Would it be also on the one line like this?"
is that non-trivial zero points of Zeta function will be on one line
==================================================
If above hypothesis is proved,
it means that arrange of prime numbers has some regular rule
in mathematical aspect
==================================================
So, in conclusion,
problem of finding rule in prime numbers
is converted into problem of proving hypothesis
saying all zero points are on the one line?
==================================================
Hardy had proved that infinite zero points would be on the one line like this
 But he didn't remove probability
that zero points could existing outside of that line
But he didn't remove probability
that zero points could existing outside of that line
 ==================================================
John Nash thought to prove Riemann hypothesis,
he could need unique way of accessing to hypothesis
==================================================
Dr. louis de branges says
understanding prime numbers is related to dynamics in micro world
==================================================
H. Montgomery found that
unlike distribution of prime numbers
which shows more irregular form of distribution
zero points (in other words gap distance between each zero point)
show more regular form of distribution
==================================================
John Nash thought to prove Riemann hypothesis,
he could need unique way of accessing to hypothesis
==================================================
Dr. louis de branges says
understanding prime numbers is related to dynamics in micro world
==================================================
H. Montgomery found that
unlike distribution of prime numbers
which shows more irregular form of distribution
zero points (in other words gap distance between each zero point)
show more regular form of distribution
 ==================================================
==================================================
 Distribution of zero points has above notation
==================================================
Above notation is similar to notation
which represents gap of energy level of nucleus of atom like Uranium
Distribution of zero points has above notation
==================================================
Above notation is similar to notation
which represents gap of energy level of nucleus of atom like Uranium
 ==================================================
==================================================
 ==================================================
==================================================
 Energy of nucleus of atom doesn't show in regular distribution
==================================================
Energy of nucleus of atom doesn't show in regular distribution
==================================================
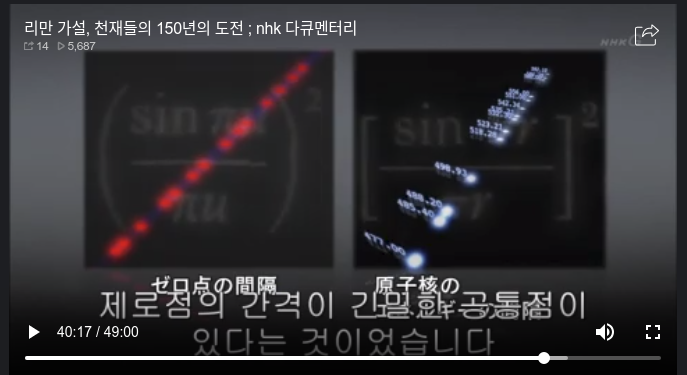 Relationship between distribution of zero points
and energy level distribution of atom
Relationship between distribution of zero points
and energy level distribution of atom


















