https://www.youtube.com/watch?v=VOfKIeTpxg8&list=PLsri7w6p16vtEz_J1G7HQG-Rm8vpZPtPS&index=5
================================================================================
4th batter in baseball
to be 4th batter, he should have batting ratio over 0.3
Criterion to be 4th batter in form of ratio: 0.3
================================================================================
Test on hypothesis about population's ratio
* AS center
* 100 customer received the service
* How many customers got satisfied by service?
* Ratio from sample: $$$\hat{p}$$$
* Ratio from population: $$$p_0$$$
$$$H_0:\hat{p}=p_0$$$
2 sided test
$$$H_1: p \ne p_0$$$
1 sided test
left
$$$H_1: p \lt p_0$$$
right
$$$H_1: p \gt p_0$$$
* test statistics on population's ratio
$$$z = \dfrac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$$$
================================================================================
* Example
* AS center
* If satisfaction ratio is >80%, no retraining on service,
otherwise, perform retraining.
* randomly selected 100 customers
* satisfied customer: 81 customers
Question
* Test population's ratio with p-value=0.05
Answer
$$$H_1: p\lt 0.8$$$
$$$H_0:p=0.8 $$$
n=100
p=0.8
$$$\alpha=0.05$$$
$$$z \\
= \frac{\hat{p}-p_0}{\sqrt{ \frac{p_0(1-p_0)}{n}}} \\
= \frac{0.81-0.8}{\sqrt{ \frac{0.8(1-0.8)}{n}}} \\
= 0.25$$$
================================================================================
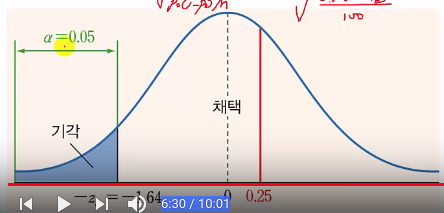 Rejection area is located in left
0.25 is located in the right
$$$H_0$$$ can't be rejected
Rejection area is located in left
0.25 is located in the right
$$$H_0$$$ can't be rejected
