https://www.youtube.com/watch?v=--lSPtpGvJ0&list=PLsri7w6p16vvQCo9pmuRNY_SYoOGB6bWM&index=5
================================================================================
 A company battery, B company battery
Unit: hour
================================================================================
$$$H_0: \bar{x}_A-\bar{x}_B = 0$$$
$$$H_1: \bar{x}_A-\bar{x}_B \ne 0$$$
n: number of sample
$$$E(\bar{x}_A-\bar{x}_b) = \mu_A-\mu_B$$$
$$$\sigma^2 \\
= s_p^2 \\
= \dfrac{(n_A-1)s_A^2 + (n_B-1)s_B^2 }{(n_A-1) + (n_B-1)} \\
= \dfrac{(20-1)\times 3.253 + (20-1)\times 2.800 }{(20-1) + (20-1)} \\
= 3.026$$$
$$$s_p^2 = 3.026$$$
$$$s_p = 1.740$$$
================================================================================
Test hypothesis
* test statistics
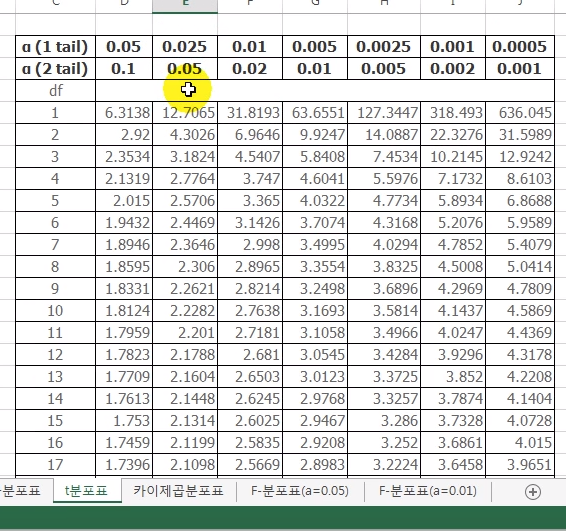
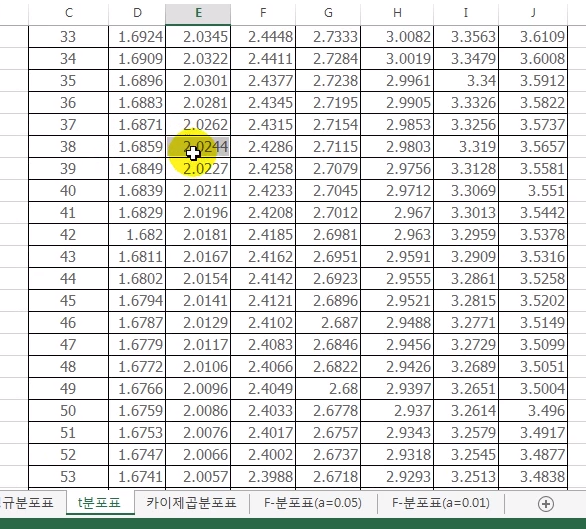
$$$t_{(n_A+n_B-2,\frac{\alpha}{2})} = \dfrac{\bar{x}_A - \bar{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}}$$$
$$$t_{(20+20-2,0.025)} = \dfrac{16.1 - 15.2}{1.740 \sqrt{\frac{1}{20} + \frac{1}{20}}} = 1.636$$$
A company battery, B company battery
Unit: hour
================================================================================
$$$H_0: \bar{x}_A-\bar{x}_B = 0$$$
$$$H_1: \bar{x}_A-\bar{x}_B \ne 0$$$
n: number of sample
$$$E(\bar{x}_A-\bar{x}_b) = \mu_A-\mu_B$$$
$$$\sigma^2 \\
= s_p^2 \\
= \dfrac{(n_A-1)s_A^2 + (n_B-1)s_B^2 }{(n_A-1) + (n_B-1)} \\
= \dfrac{(20-1)\times 3.253 + (20-1)\times 2.800 }{(20-1) + (20-1)} \\
= 3.026$$$
$$$s_p^2 = 3.026$$$
$$$s_p = 1.740$$$
================================================================================
Test hypothesis
* test statistics
$$$t_{(n_A+n_B-2,\frac{\alpha}{2})} = \dfrac{\bar{x}_A - \bar{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}}$$$
$$$t_{(20+20-2,0.025)} = \dfrac{16.1 - 15.2}{1.740 \sqrt{\frac{1}{20} + \frac{1}{20}}} = 1.636$$$
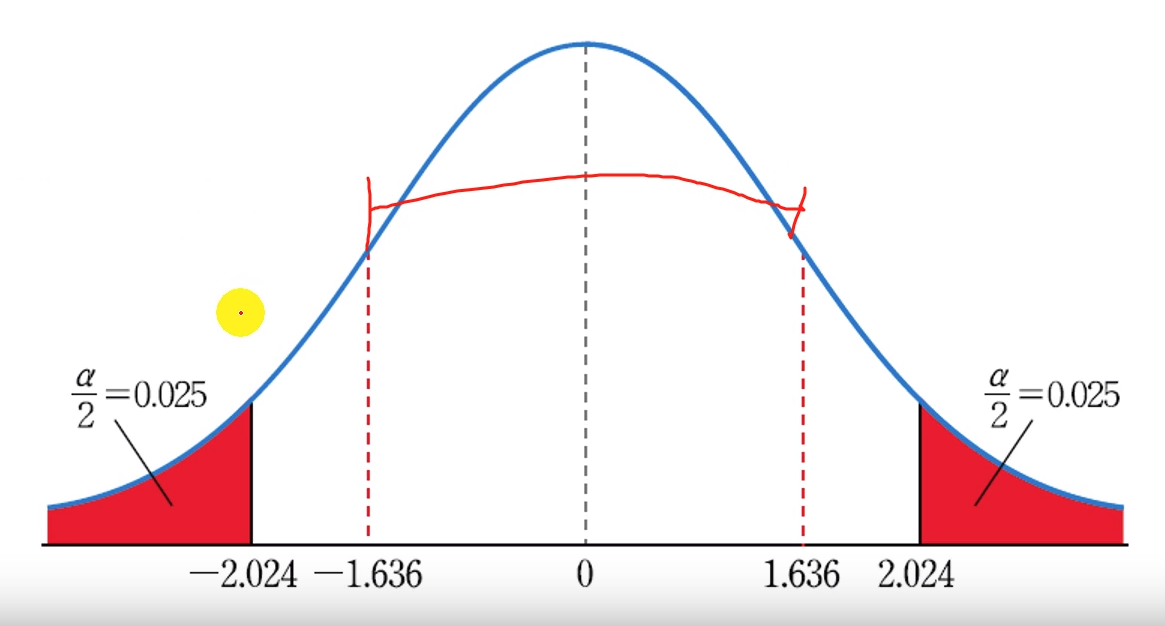 * center between dot vertical lines: test statistics region
* center between dot vertical lines: test statistics region
 * wide interval: trusted region
$$$(16.1-15.2)-1.636 \times 1.740 \times \sqrt{\frac{1}{20}+\frac{1}{20}}
\le \mu_A-\mu_B
\le (16.1-15.2)+1.636 \times 1.740 \times \sqrt{\frac{1}{20}+\frac{1}{20}}$$$
* wide interval: trusted region
$$$(16.1-15.2)-1.636 \times 1.740 \times \sqrt{\frac{1}{20}+\frac{1}{20}}
\le \mu_A-\mu_B
\le (16.1-15.2)+1.636 \times 1.740 \times \sqrt{\frac{1}{20}+\frac{1}{20}}$$$
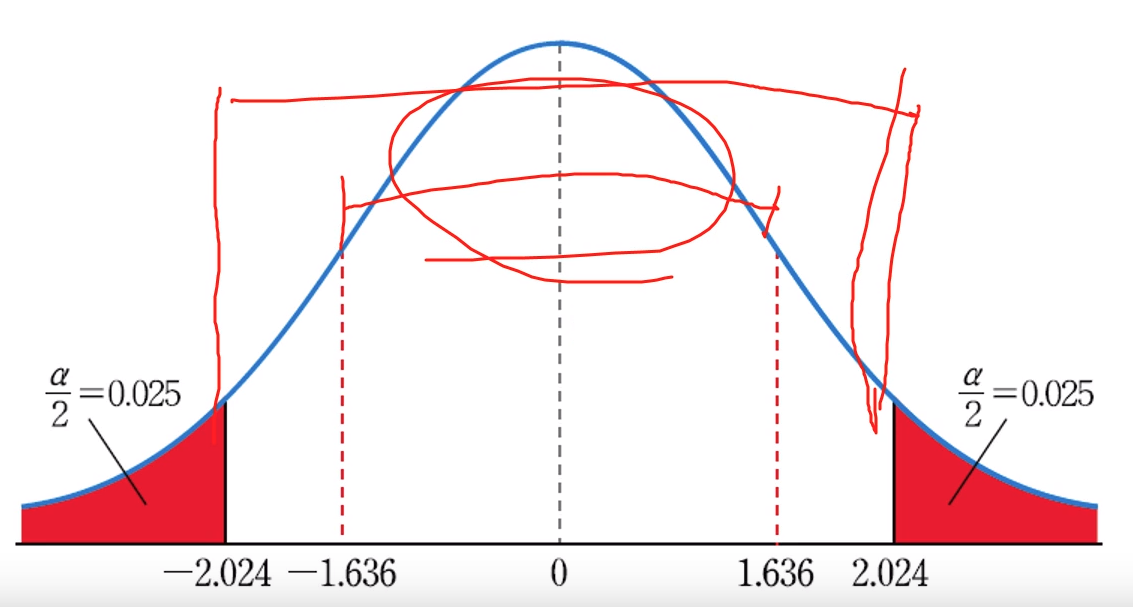
 test statistics region $$$\subset$$$ trusted region
* Trusted region
$$$(\bar{x}_A - \bar{x}_B) - t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}
\le \mu_A-\mu_B
\le (\bar{x}_A - \bar{x}_B) + t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}$$$
$$$(\bar{x}_A - \bar{x}_B) - t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}
\le \mu_A-\mu_B
\le (\bar{x}_A - \bar{x}_B) + t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}$$$
test statistics region $$$\subset$$$ trusted region
* Trusted region
$$$(\bar{x}_A - \bar{x}_B) - t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}
\le \mu_A-\mu_B
\le (\bar{x}_A - \bar{x}_B) + t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}$$$
$$$(\bar{x}_A - \bar{x}_B) - t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}
\le \mu_A-\mu_B
\le (\bar{x}_A - \bar{x}_B) + t_{(n_A+n_B-2,\frac{\alpha}{2})} \times s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}$$$






