https://www.youtube.com/watch?v=htXELssWGEk&list=PLsri7w6p16vsOVj5cL8U4z0m4RdMZfhme&index=2
================================================================================
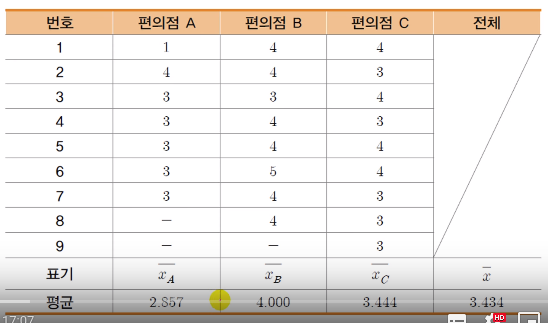
$$$H_0$$$: no difference, $$$\bar{x}_A = \bar{x}_B = \bar{x}_C$$$
$$$H_1$$$: there is difference, other cases
================================================================================
 ================================================================================
================================================================================
 Sum of squares total (SST)
$$$SST = \sum\sum (x_{ij}-\bar{x})^2$$$
$$$(1-3.434)^2+(4-3.434)^2+\cdots+ (3-3.434)^2 = 13.973$$$
================================================================================
Sum of squares between samples (SSB)
Sum of squares total (SST)
$$$SST = \sum\sum (x_{ij}-\bar{x})^2$$$
$$$(1-3.434)^2+(4-3.434)^2+\cdots+ (3-3.434)^2 = 13.973$$$
================================================================================
Sum of squares between samples (SSB)
 $$$SSB = \sum n_i (\bar{x}_j - \bar{x})^2$$$
$$$ 7(2.857-3.434)^2 + 8(4.000-3.434)^2 + 9(3.444-3.434)^2 = 4.894$$$
================================================================================
Sum of squares within samples (SSW)
$$$SSB = \sum n_i (\bar{x}_j - \bar{x})^2$$$
$$$ 7(2.857-3.434)^2 + 8(4.000-3.434)^2 + 9(3.444-3.434)^2 = 4.894$$$
================================================================================
Sum of squares within samples (SSW)
 $$$SSW = \sum\sum (x_{ij} - \bar{x}_i)^2$$$
$$$SSW_A=(1-2.857)^2+(4-2.857)^2+(3-2.857)^2=4.857$$$
$$$SSW_B=(4-4.000)^2+(4-4.000)^2+(4-4.000)^2=2.000$$$
$$$SSW_C=(4-3.444)^2+(3-3.444)^2+(3-3.444)^2=2.222$$$
$$$SSW = 4.857+2.000+2.222 = 9.079$$$
================================================================================
$$$SSW = \sum\sum (x_{ij} - \bar{x}_i)^2$$$
$$$SSW_A=(1-2.857)^2+(4-2.857)^2+(3-2.857)^2=4.857$$$
$$$SSW_B=(4-4.000)^2+(4-4.000)^2+(4-4.000)^2=2.000$$$
$$$SSW_C=(4-3.444)^2+(3-3.444)^2+(3-3.444)^2=2.222$$$
$$$SSW = 4.857+2.000+2.222 = 9.079$$$
================================================================================
 ================================================================================
When you compare some values, basic values are mean value
Degree of freedom of SST: n-1
Degree of freedom of SSB: i-1
Degree of freedom of SSW: n-i
================================================================================
Mean square of between samples (MBS)
$$$MBS = \frac{\text{SSB}}{i-1}$$$
Mean square of within samples (MSW)
$$$MSW = \frac{\text{SSW}}{n-i}$$$
================================================================================
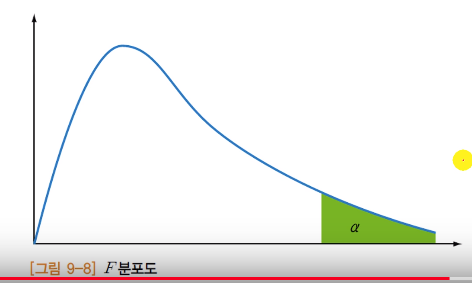
Ratio of variance (F)
$$$F \\
= \dfrac{\text{change between classes}}{\text{changes within classes}} \\
= \dfrac{MSB}{MSW} \\
= \dfrac{\frac{SSB}{i-1}}{\frac{SSW}{n-i}}$$$
================================================================================
$$$MSB = \dfrac{4.894}{2} = 2.447$$$
$$$MSW = \dfrac{9.079}{21} = 0.432$$$
$$$F = \dfrac{2.447}{0.432} = 5.664$$$
================================================================================
One-way ANOVA table report
================================================================================
When you compare some values, basic values are mean value
Degree of freedom of SST: n-1
Degree of freedom of SSB: i-1
Degree of freedom of SSW: n-i
================================================================================
Mean square of between samples (MBS)
$$$MBS = \frac{\text{SSB}}{i-1}$$$
Mean square of within samples (MSW)
$$$MSW = \frac{\text{SSW}}{n-i}$$$
================================================================================
Ratio of variance (F)
$$$F \\
= \dfrac{\text{change between classes}}{\text{changes within classes}} \\
= \dfrac{MSB}{MSW} \\
= \dfrac{\frac{SSB}{i-1}}{\frac{SSW}{n-i}}$$$
================================================================================
$$$MSB = \dfrac{4.894}{2} = 2.447$$$
$$$MSW = \dfrac{9.079}{21} = 0.432$$$
$$$F = \dfrac{2.447}{0.432} = 5.664$$$
================================================================================
One-way ANOVA table report
 ================================================================================
================================================================================

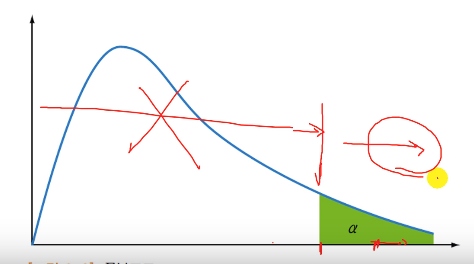 $$$H_0$$$ is rejected
$$$H_0$$$ is rejected








