https://www.youtube.com/watch?v=TtqUCUr711s&list=PLsri7w6p16vsOVj5cL8U4z0m4RdMZfhme&index=3
================================================================================
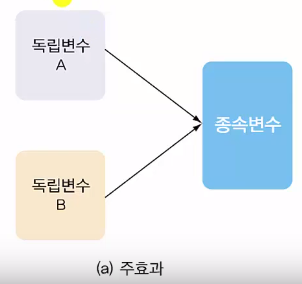 Effect of "brand" to "satisfaction"
Effect of "region" to "satisfaction"
================================================================================
Effect of "brand" to "satisfaction"
Effect of "region" to "satisfaction"
================================================================================
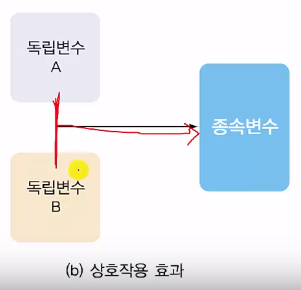 Even if A and B are independent,
A and B can affect "interation effect" to "dependent variable" like satisfaction
So, effects are A, B, A+B
================================================================================
Even if A and B are independent,
A and B can affect "interation effect" to "dependent variable" like satisfaction
So, effects are A, B, A+B
================================================================================
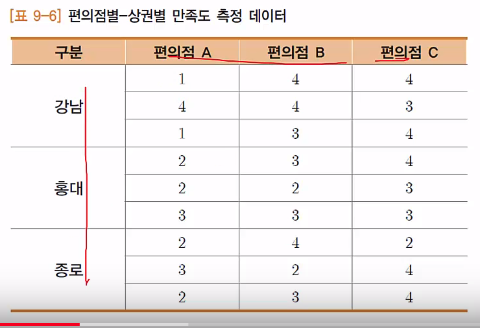 2 independent variables
Numbers: satisfaction
Question: there is difference in "satisfaction" wrt "2 variables"
using $$$\alpha=0.05$$$?
================================================================================
Establish hypothesis
$$$\bar{x}$$$: mean of entire
$$$\bar{x}_i$$$: mean of each conveninet store
$$$\bar{x}_j$$$: mean of each conveninet store's location
$$$\bar{x}_{ij}$$$: 2 independent variables
$$$\bar{x}_{ijk}$$$: 2 independent variables, kth observation
================================================================================
2 independent variables
Numbers: satisfaction
Question: there is difference in "satisfaction" wrt "2 variables"
using $$$\alpha=0.05$$$?
================================================================================
Establish hypothesis
$$$\bar{x}$$$: mean of entire
$$$\bar{x}_i$$$: mean of each conveninet store
$$$\bar{x}_j$$$: mean of each conveninet store's location
$$$\bar{x}_{ij}$$$: 2 independent variables
$$$\bar{x}_{ijk}$$$: 2 independent variables, kth observation
================================================================================
 i: conveninet store A,B,C
j: location, KangNam, HongDae, JongRo
k: kth satisfaction
================================================================================
i: conveninet store A,B,C
j: location, KangNam, HongDae, JongRo
k: kth satisfaction
================================================================================
 ================================================================================
$$$SST = (1-2.926)^2 + (4-2.926)^2 + \cdots + (4-2.926)^2 = 23.862$$$
$$$SSB_i = 9(2.228-2.926)^2 + 9(3.111-2.926)^2 + \cdots + 9(3.444-2.926)^2 = 7.183$$$
$$$SSB_j = 9(3.111-2.926)^2 + 9(2.778-2.926)^2 + \cdots + 9(2.889-2.926)^2 = 0.517$$$
Interaction
$$$SSB_{ij} = 3(2.000-2.222-3.111+2.926)^2 + \cdots + 3(3.333-3.444-2.889+2.926)^2 = 1.481$$$
$$$SSW = SST - SSB_i - SSB_j - SSB_{ij} = 14.671$$$
================================================================================
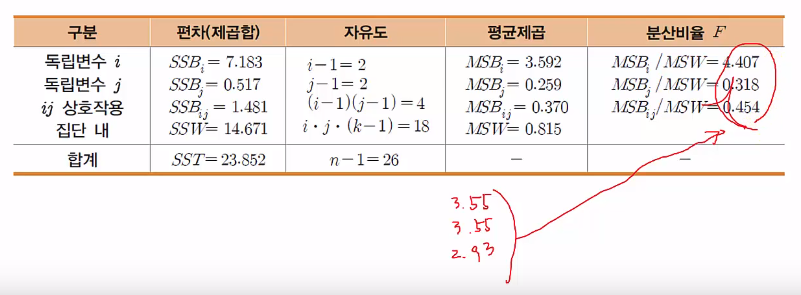
$$$MSB_i = \dfrac{SSB_i}{i-1} = \dfrac{7.183}{3-1} = 3.592$$$
$$$MSB_i = \dfrac{SSB_j}{j-1} = \dfrac{0.517}{3-1} = 0.259$$$
$$$MSB_{ij} = \dfrac{SSB_{ij}}{(i-1)(j-1)} = \dfrac{1.481}{(3-1)(3-1)} = 0.370$$$
$$$MSW = \dfrac{SSW}{i\times j \times (k-1)} = \dfrac{14.671}{3\times 3 \times 2}=0.815$$$
================================================================================
================================================================================
$$$SST = (1-2.926)^2 + (4-2.926)^2 + \cdots + (4-2.926)^2 = 23.862$$$
$$$SSB_i = 9(2.228-2.926)^2 + 9(3.111-2.926)^2 + \cdots + 9(3.444-2.926)^2 = 7.183$$$
$$$SSB_j = 9(3.111-2.926)^2 + 9(2.778-2.926)^2 + \cdots + 9(2.889-2.926)^2 = 0.517$$$
Interaction
$$$SSB_{ij} = 3(2.000-2.222-3.111+2.926)^2 + \cdots + 3(3.333-3.444-2.889+2.926)^2 = 1.481$$$
$$$SSW = SST - SSB_i - SSB_j - SSB_{ij} = 14.671$$$
================================================================================
$$$MSB_i = \dfrac{SSB_i}{i-1} = \dfrac{7.183}{3-1} = 3.592$$$
$$$MSB_i = \dfrac{SSB_j}{j-1} = \dfrac{0.517}{3-1} = 0.259$$$
$$$MSB_{ij} = \dfrac{SSB_{ij}}{(i-1)(j-1)} = \dfrac{1.481}{(3-1)(3-1)} = 0.370$$$
$$$MSW = \dfrac{SSW}{i\times j \times (k-1)} = \dfrac{14.671}{3\times 3 \times 2}=0.815$$$
================================================================================

 ================================================================================
================================================================================






