This is personal study note
Copyright and original reference are from:
https://www.dropbox.com/s/d9zacj2zgvy8142/Class2_2019_theory.pptx?dl=0#
================================================================================
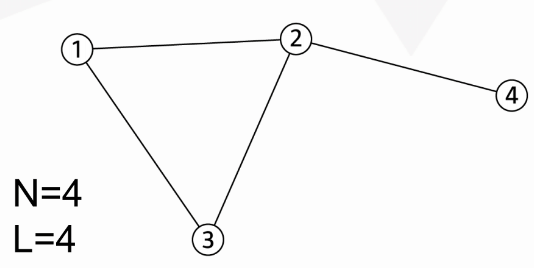
"Components" of a "complex system"
 components: red circles, nodes or vertices, N
interactions: black lines, links or edges, L
system: network or graph, (N,L)
================================================================================
components: red circles, nodes or vertices, N
interactions: black lines, links or edges, L
system: network or graph, (N,L)
================================================================================
 ================================================================================
"A node" degree: the number of links connected to the "A node"
================================================================================
"A node" degree: the number of links connected to the "A node"
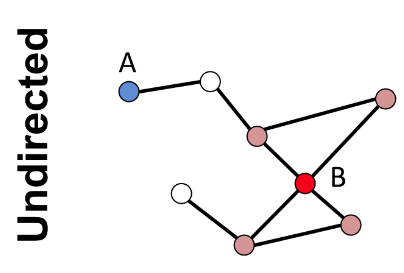 $$$k_A=1$$$
$$$k_B=4$$$
$$$k_A=1$$$
$$$k_B=4$$$
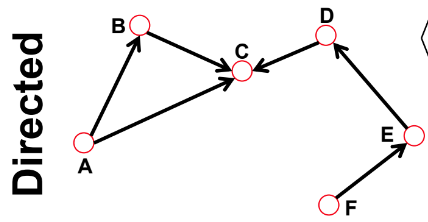
 In directed graph, there are "in degree" and "out degree"
Total degree = "in degree" + "out degree"
$$$k_C^{in}$$$=2
$$$k_C^{out}$$$=1
$$$k_C^{total}$$$=3
================================================================================
Source (in directed graph) means the node which has $$$k^{in}=0$$$
Sink (in directed graph) means the node which has $$$k^{out}=0$$$
================================================================================
In directed graph, there are "in degree" and "out degree"
Total degree = "in degree" + "out degree"
$$$k_C^{in}$$$=2
$$$k_C^{out}$$$=1
$$$k_C^{total}$$$=3
================================================================================
Source (in directed graph) means the node which has $$$k^{in}=0$$$
Sink (in directed graph) means the node which has $$$k^{out}=0$$$
================================================================================
 ================================================================================
Average degree
================================================================================
Average degree
 $$$\left<k\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i$$$
N: number of nodes in the graph
$$$\left<k\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i$$$
N: number of nodes in the graph
 $$$\left<k^{in}\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i^{in}$$$
$$$\left<k^{out}\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i^{out}$$$
$$$\left<k^{in}\right>=\left<k^{out}\right>$$$
================================================================================
Degree distribution
case1
$$$\left<k^{in}\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i^{in}$$$
$$$\left<k^{out}\right> = \frac{1}{N} \sum\limits_{N}^{i=1}k_i^{out}$$$
$$$\left<k^{in}\right>=\left<k^{out}\right>$$$
================================================================================
Degree distribution
case1
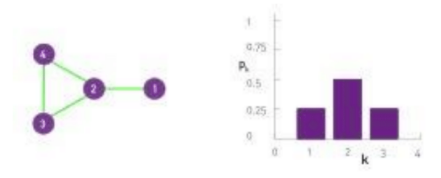 case2
case2
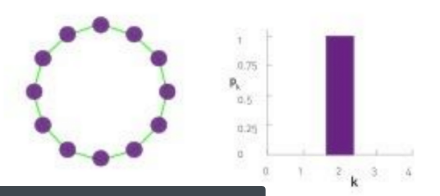 $$$P(k)$$$: probability that a "randomly chosen node" has "degree k"
$$$N_k$$$: the number of nodes which have degree k
$$$P(k) = \dfrac{N_k}{N} $$$
================================================================================
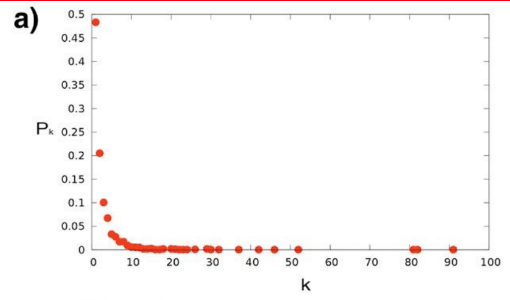
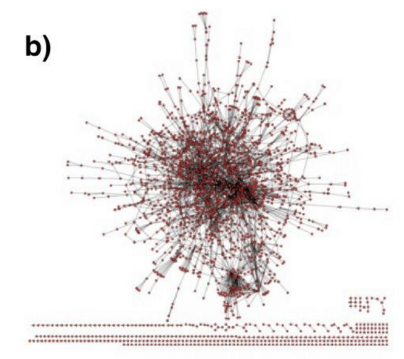
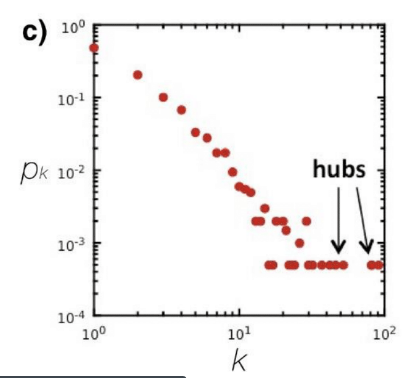
Degree distribution examples
$$$P(k)$$$: probability that a "randomly chosen node" has "degree k"
$$$N_k$$$: the number of nodes which have degree k
$$$P(k) = \dfrac{N_k}{N} $$$
================================================================================
Degree distribution examples
 ================================================================================
Degree distribution
- Discrete representation:
$$$p_k$$$ is the probability that a "node" has degree k
- Continuum description:
$$$p_k$$$ is the PDF of the degrees, where
$$$\int_{k_1}^{k_2} p(k) dk$$$
$$$\int_{k_1}^{k_2} p(k) dk$$$ represents the probability that a "node's degree" is between $$$k_1$$$ and $$$k_2$$$
- Normalization condition:
$$$\sum\limits_{0}^{\infty}p_k=1$$$
$$$\int_{k_{min}}^{\infty} p(k) dk = 1$$$
$$$k_{min}$$$: minimal degree in the network
================================================================================
Undirected network vs. Directed network
Undirected network
================================================================================
Degree distribution
- Discrete representation:
$$$p_k$$$ is the probability that a "node" has degree k
- Continuum description:
$$$p_k$$$ is the PDF of the degrees, where
$$$\int_{k_1}^{k_2} p(k) dk$$$
$$$\int_{k_1}^{k_2} p(k) dk$$$ represents the probability that a "node's degree" is between $$$k_1$$$ and $$$k_2$$$
- Normalization condition:
$$$\sum\limits_{0}^{\infty}p_k=1$$$
$$$\int_{k_{min}}^{\infty} p(k) dk = 1$$$
$$$k_{min}$$$: minimal degree in the network
================================================================================
Undirected network vs. Directed network
Undirected network
 - Link: undirected (symmetrical)
- Undirected links example:
- Coauthorship links
- Actor network
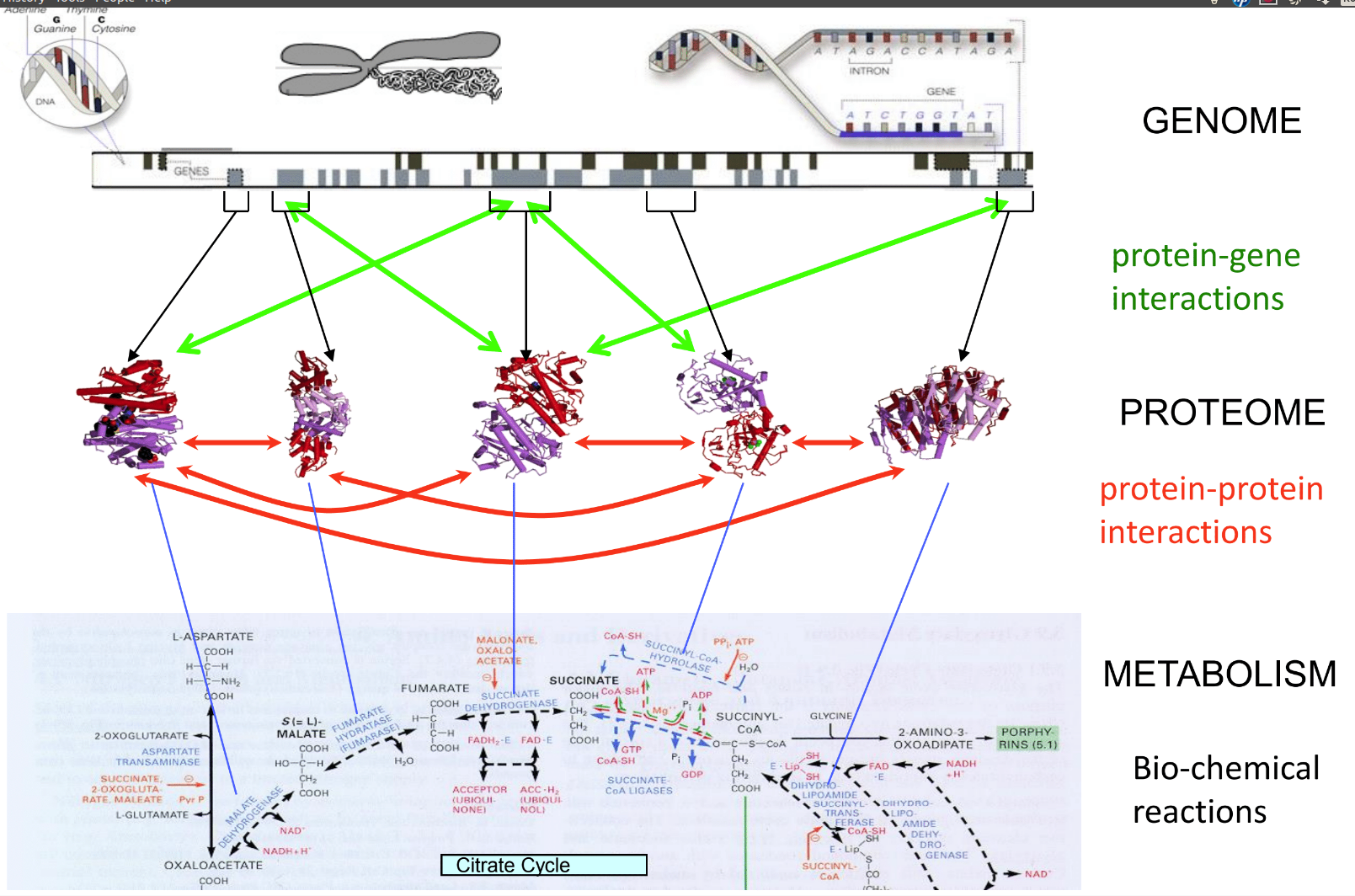
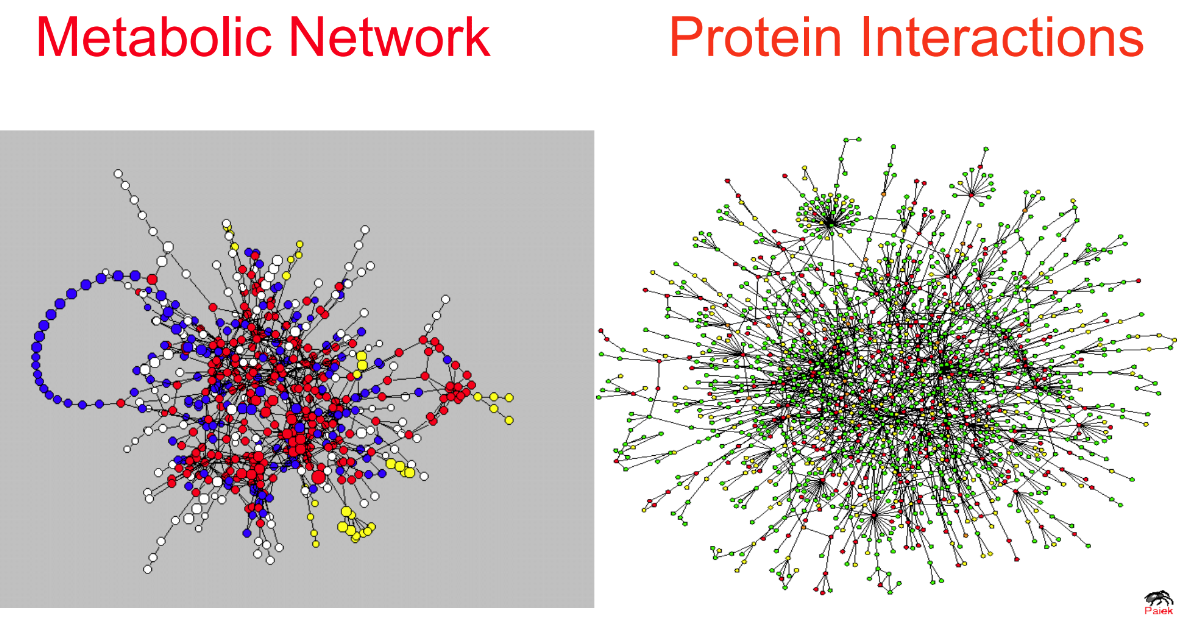
- Protein interactions
================================================================================
Directed network
- Link: undirected (symmetrical)
- Undirected links example:
- Coauthorship links
- Actor network
- Protein interactions
================================================================================
Directed network
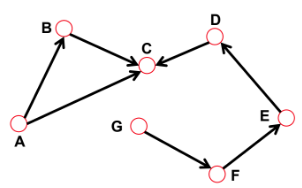 - Links: directed (arcs)
- Digraph means "directed graph"
- Directed links example:
- Phone calls
- Metabolic reactions
================================================================================
Adjacency matrix
If there is a link between "node i" and "node j"
$$$A_{ij}=1$$$
If "node i" and "node j" are not connected to each other
$$$A_{ij}=0$$$
- Links: directed (arcs)
- Digraph means "directed graph"
- Directed links example:
- Phone calls
- Metabolic reactions
================================================================================
Adjacency matrix
If there is a link between "node i" and "node j"
$$$A_{ij}=1$$$
If "node i" and "node j" are not connected to each other
$$$A_{ij}=0$$$
 A_{ij} = \begin{bmatrix} 0&&1&&0&&1\\1&&0&&0&&1\\0&&0&&0&&1\\1&&1&&1&&0 \end{bmatrix}
================================================================================
If there is a link pointing from "node j" and "node i"
$$$A_{ij}=1$$$
If there is no link pointing from "node i" and "node j"
$$$A_{ij}=0$$$
A_{ij} = \begin{bmatrix} 0&&1&&0&&1\\1&&0&&0&&1\\0&&0&&0&&1\\1&&1&&1&&0 \end{bmatrix}
================================================================================
If there is a link pointing from "node j" and "node i"
$$$A_{ij}=1$$$
If there is no link pointing from "node i" and "node j"
$$$A_{ij}=0$$$
 A_{ij} = \begin{bmatrix} 0&&0&&0&&0\\1&&0&&0&&1\\0&&0&&0&&1\\1&&0&&0&&0 \end{bmatrix}
Note that "for a directed graph", the adjacency matrix is not symmetric
================================================================================
Adjacency matrix and node degrees
A_{ij} = \begin{bmatrix} 0&&0&&0&&0\\1&&0&&0&&1\\0&&0&&0&&1\\1&&0&&0&&0 \end{bmatrix}
Note that "for a directed graph", the adjacency matrix is not symmetric
================================================================================
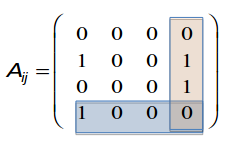
Adjacency matrix and node degrees

 Red square: $$$A_{21}=1, A_{22}=0, A_{23}=0, A_{24}=1$$$
Blue square: $$$A_{12}=1, A_{22}=0, A_{32}=0, A_{42}=1$$$
Conclusion1: $$$A_{ij}=A_{ji}$$$
Conclusion2: $$$A_{ii}=0$$$
Conclusion3: $$$k_i = \sum\limits_{j=1}^{N} A_{ij}$$$
Conclusion4: $$$k_j = \sum\limits_{i=1}^{N} A_{ij}$$$
Conclusion5: $$$L = \frac{1}{2} \sum\limits_{i=1}^{N}k_i = \frac{1}{2} \sum\limits_{ij}^{N}A_{ij} $$$
================================================================================
Adjacency matrix and node degrees
Red square: $$$A_{21}=1, A_{22}=0, A_{23}=0, A_{24}=1$$$
Blue square: $$$A_{12}=1, A_{22}=0, A_{32}=0, A_{42}=1$$$
Conclusion1: $$$A_{ij}=A_{ji}$$$
Conclusion2: $$$A_{ii}=0$$$
Conclusion3: $$$k_i = \sum\limits_{j=1}^{N} A_{ij}$$$
Conclusion4: $$$k_j = \sum\limits_{i=1}^{N} A_{ij}$$$
Conclusion5: $$$L = \frac{1}{2} \sum\limits_{i=1}^{N}k_i = \frac{1}{2} \sum\limits_{ij}^{N}A_{ij} $$$
================================================================================
Adjacency matrix and node degrees
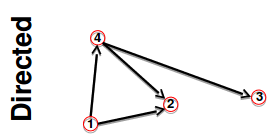
 Red square: $$$A_{14}=0, A_{24}=1, A_{34}=1, A_{44}=0$$$
Blue square: $$$A_{41}=1, A_{42}=0, A_{43}=0, A_{44}=0$$$
Conclusion1: $$$A_{ij} \ne A_{ji}$$$
Conclusion2: $$$A_{ii}=0$$$
Conclusion3: $$$k_i^{in} = \sum\limits_{j=1}^{N} A_{ij}$$$
Conclusion4: $$$k_j^{out} = \sum\limits_{i=1}^{N} A_{ij}$$$
Conclusion5: $$$L = \sum\limits_{i=1}^{N} k_i^{in} = \sum\limits_{j=1}^{N} k_j^{out} = \sum\limits_{i,j}^{N} A_{ij} $$$
================================================================================
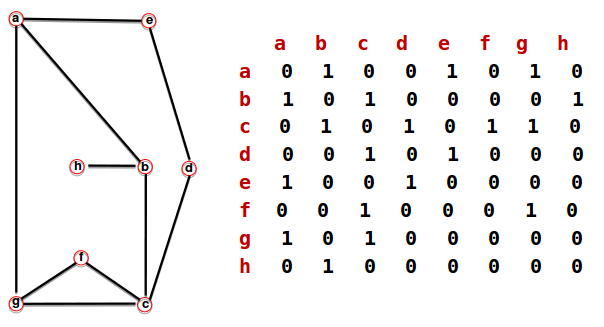
Adjacency matrix of complicated graph
Red square: $$$A_{14}=0, A_{24}=1, A_{34}=1, A_{44}=0$$$
Blue square: $$$A_{41}=1, A_{42}=0, A_{43}=0, A_{44}=0$$$
Conclusion1: $$$A_{ij} \ne A_{ji}$$$
Conclusion2: $$$A_{ii}=0$$$
Conclusion3: $$$k_i^{in} = \sum\limits_{j=1}^{N} A_{ij}$$$
Conclusion4: $$$k_j^{out} = \sum\limits_{i=1}^{N} A_{ij}$$$
Conclusion5: $$$L = \sum\limits_{i=1}^{N} k_i^{in} = \sum\limits_{j=1}^{N} k_j^{out} = \sum\limits_{i,j}^{N} A_{ij} $$$
================================================================================
Adjacency matrix of complicated graph
 ================================================================================
Adjacency matrices are sparse
================================================================================
Adjacency matrices are sparse
 ================================================================================
Real networks are sparse
================================================================================
================================================================================
Real networks are sparse
================================================================================
 The maximum number of links which a "network having N nodes" can have is:
$$$L_{max} = \begin{pmatrix} N\\2 \end{pmatrix} = \dfrac{N(N-1)}{2}$$$
================================================================================
Complete graph: Number_of_lines_L = L_max
Average degree of complete graph: $$$\left< k \right> =N-1 $$$
================================================================================
Most networks which are observed in real systems are sparse:
Number_of_lines_L << L_max or
$$$\left< k \right> << N-1 $$$
- Example
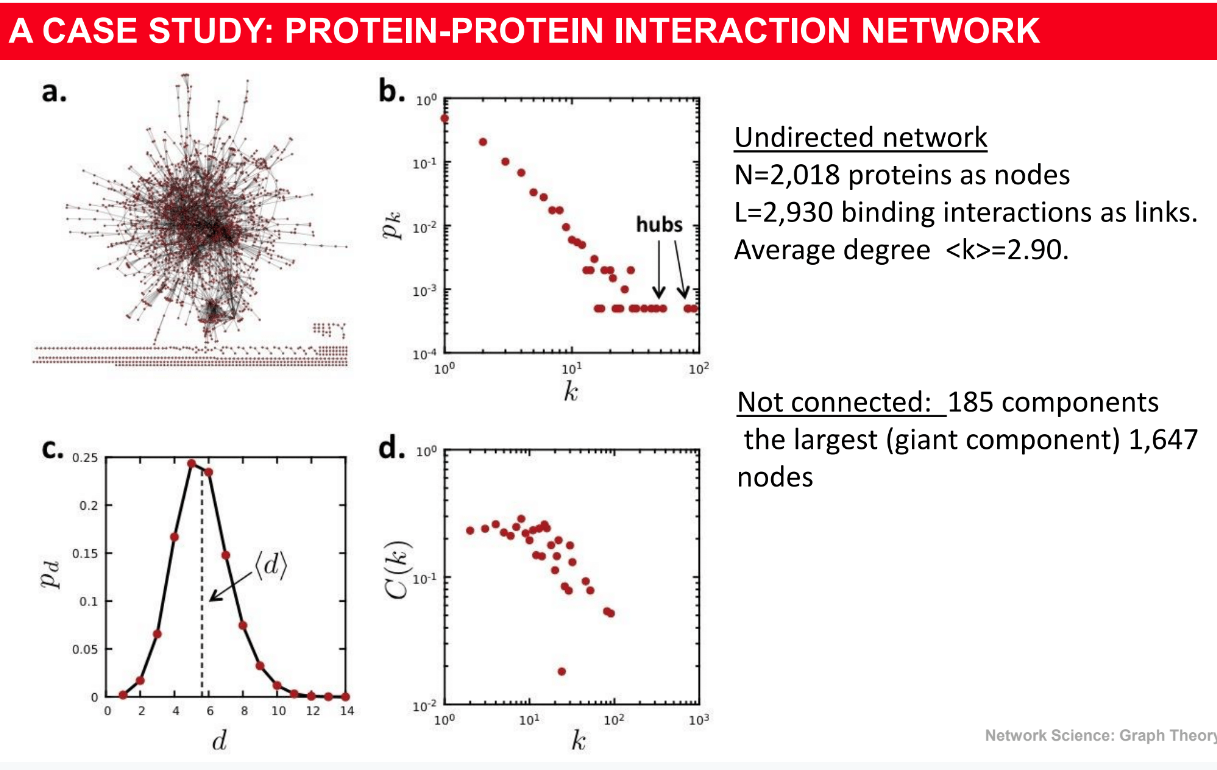
Protein (S. Cerevisiae):
N=1,870
L=4,470
L_max=$$$10^7$$$
<k>=2.39
================================================================================
Adjacency matrices are sparse
The maximum number of links which a "network having N nodes" can have is:
$$$L_{max} = \begin{pmatrix} N\\2 \end{pmatrix} = \dfrac{N(N-1)}{2}$$$
================================================================================
Complete graph: Number_of_lines_L = L_max
Average degree of complete graph: $$$\left< k \right> =N-1 $$$
================================================================================
Most networks which are observed in real systems are sparse:
Number_of_lines_L << L_max or
$$$\left< k \right> << N-1 $$$
- Example
Protein (S. Cerevisiae):
N=1,870
L=4,470
L_max=$$$10^7$$$
<k>=2.39
================================================================================
Adjacency matrices are sparse
 ================================================================================
Metcalfe’s law
================================================================================
Metcalfe’s law

 The maximum number of links which a "network of N nodes" can have is
$$$L_{max} = \begin{pmatrix} N\\2 \end{pmatrix} = \dfrac{N(N-1)}{2}$$$
================================================================================
Bipartite networks (or bigraph)
It is the graph whose nodes can be divided into 2 disjoint sets U and V,
such that "every link" connects a "node in U" to "one in V"
that is, U and V are independent sets
The maximum number of links which a "network of N nodes" can have is
$$$L_{max} = \begin{pmatrix} N\\2 \end{pmatrix} = \dfrac{N(N-1)}{2}$$$
================================================================================
Bipartite networks (or bigraph)
It is the graph whose nodes can be divided into 2 disjoint sets U and V,
such that "every link" connects a "node in U" to "one in V"
that is, U and V are independent sets
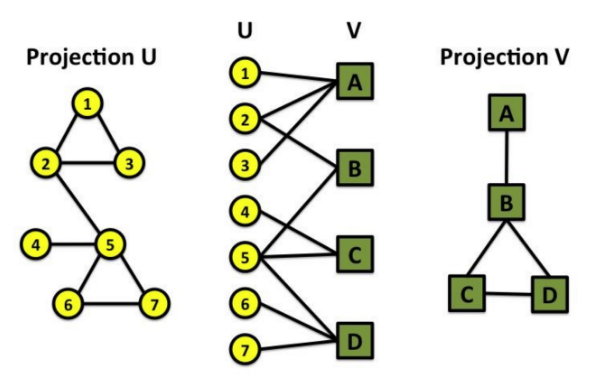 - Example
- Hollywood actor network
- Collaboration network
- Disease network (diseasome)
================================================================================
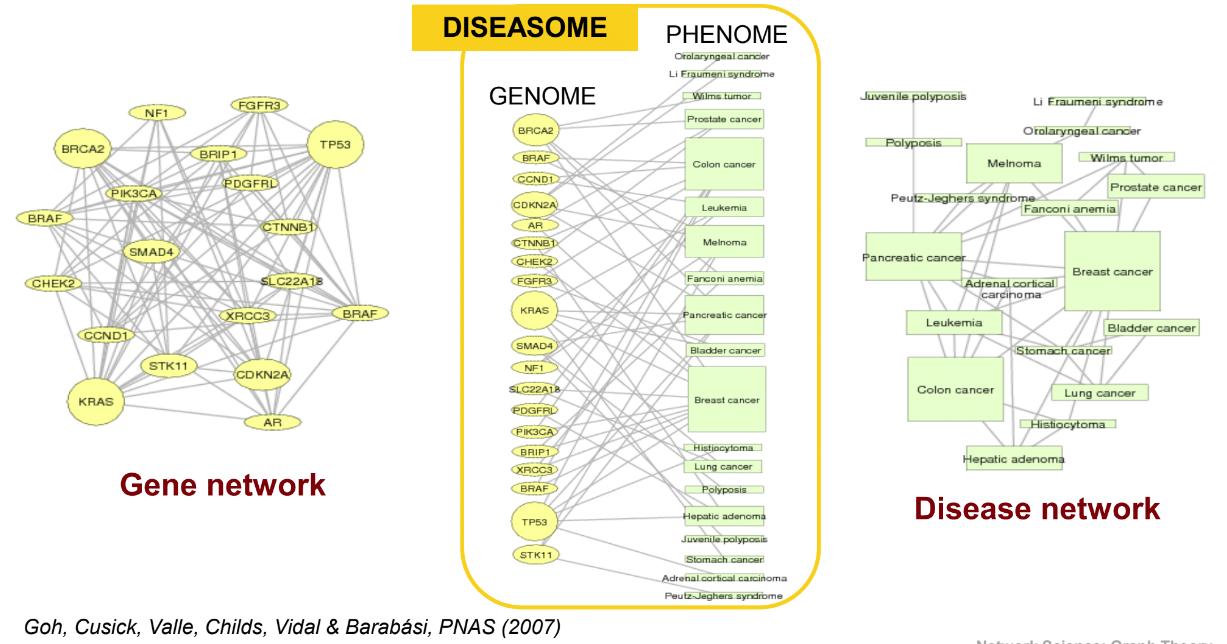
Gene network (U) and disease network (V)
- Example
- Hollywood actor network
- Collaboration network
- Disease network (diseasome)
================================================================================
Gene network (U) and disease network (V)
 ================================================================================
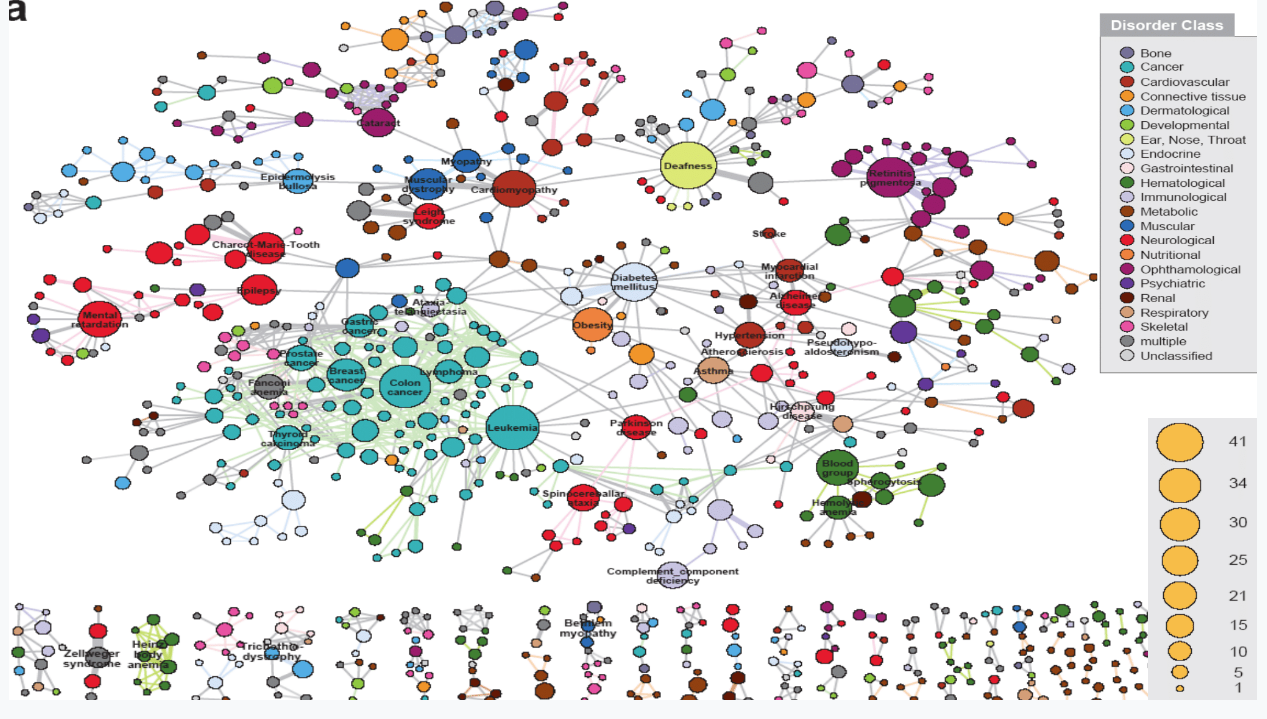
Human disease network
================================================================================
Human disease network
 ================================================================================
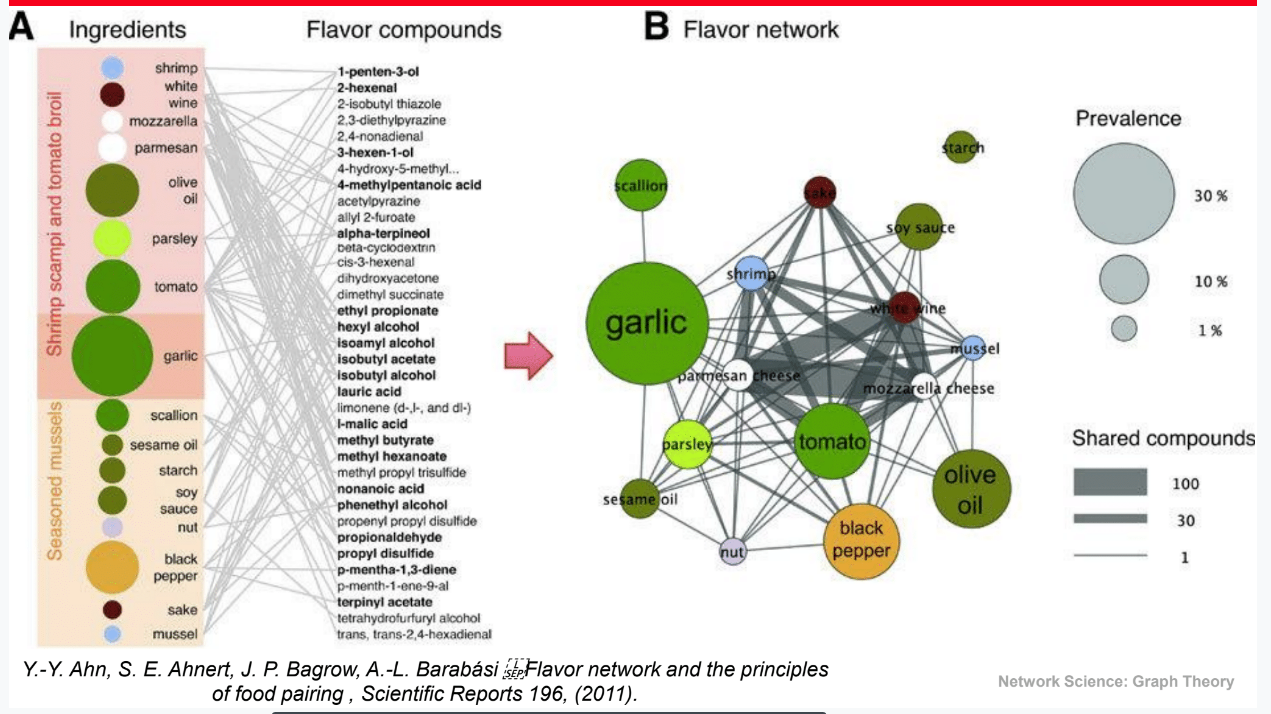
Ingredient (U) and Flavor compounds (V) // Flavor network
================================================================================
Ingredient (U) and Flavor compounds (V) // Flavor network
 ================================================================================
================================================================================
 ================================================================================
"Path" is a "sequence of nodes" in which each node is adjacent to the next one
$$$P_{i0,in}$$$ of length n between nodes $$$i_0$$$ and $$$i_n$$$ is an ordered collection of n+1 nodes and n links
2 expressions of path
$$$P_n = \{i_0,i_1,i_2,\cdots,i_n\}$$$
$$$P_n = \{(i_0,i_1),(i_1,i_2),(i_2,i_3),\cdots,(i_{n-1},i_{n})\}$$$
================================================================================
Path example in the graph
================================================================================
"Path" is a "sequence of nodes" in which each node is adjacent to the next one
$$$P_{i0,in}$$$ of length n between nodes $$$i_0$$$ and $$$i_n$$$ is an ordered collection of n+1 nodes and n links
2 expressions of path
$$$P_n = \{i_0,i_1,i_2,\cdots,i_n\}$$$
$$$P_n = \{(i_0,i_1),(i_1,i_2),(i_2,i_3),\cdots,(i_{n-1},i_{n})\}$$$
================================================================================
Path example in the graph
 ================================================================================
In a directed network, the path can follow only the direction of an arrow
================================================================================
- Distance (shortest path, geodesic path) between 2 nodes is defined as "the number of edges"
along the shortest path connecting them
- If the 2 nodes are disconnected, the distance is infinity
================================================================================
In a directed network, the path can follow only the direction of an arrow
================================================================================
- Distance (shortest path, geodesic path) between 2 nodes is defined as "the number of edges"
along the shortest path connecting them
- If the 2 nodes are disconnected, the distance is infinity
 ================================================================================
In "directed graphs", "each path" needs to follow the "direction of the arrows".
Thus, in a digraph, the "distance from node A to node B" (on an AB path) is
generally different from the distance from node B to A (on a BCA path).
================================================================================
In "directed graphs", "each path" needs to follow the "direction of the arrows".
Thus, in a digraph, the "distance from node A to node B" (on an AB path) is
generally different from the distance from node B to A (on a BCA path).
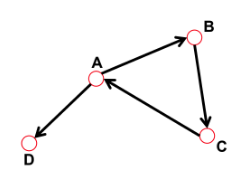 ================================================================================
Number of paths between two nodes - adjacency matrix
$$$N_{ij}$$$: the number of paths between any 2 nodes i and j
- If there is a link between "node i" and "node j", then $$$A_ij=1$$$ and $$$A_{ij}=0$$$ otherwise
Length n=1:
- If there is a path of length two between "node i" and "node j", then $$$A_{ik}A_{kj}=1$$$, and $$$A_{ik}A_{kj}=0$$$ otherwise.
Length n=2:
The number of paths of length 2:
$$$N_{ij}^{(2)} = \sum\limits_{k=1}^{N} A_{ik}A_{kj} = [A^2]_{ij} $$$
- In general, if there is a path of length n between "node i" and "node j",
then $$$A_{ik} \cdots A_{lj}=1$$$ and $$$A_{ik} \cdots A_{lj} = 0$$$ otherwise.
Length n
The number of paths of length n between i and j is (holds for both directed and undirected networks.)
$$$N_{ij}^{(n)} = [A^n]_{ij}$$$
================================================================================
Finding distances: breadth first search
- Find the distance between "node 0" and "node 4"
step1. start at 0
================================================================================
Number of paths between two nodes - adjacency matrix
$$$N_{ij}$$$: the number of paths between any 2 nodes i and j
- If there is a link between "node i" and "node j", then $$$A_ij=1$$$ and $$$A_{ij}=0$$$ otherwise
Length n=1:
- If there is a path of length two between "node i" and "node j", then $$$A_{ik}A_{kj}=1$$$, and $$$A_{ik}A_{kj}=0$$$ otherwise.
Length n=2:
The number of paths of length 2:
$$$N_{ij}^{(2)} = \sum\limits_{k=1}^{N} A_{ik}A_{kj} = [A^2]_{ij} $$$
- In general, if there is a path of length n between "node i" and "node j",
then $$$A_{ik} \cdots A_{lj}=1$$$ and $$$A_{ik} \cdots A_{lj} = 0$$$ otherwise.
Length n
The number of paths of length n between i and j is (holds for both directed and undirected networks.)
$$$N_{ij}^{(n)} = [A^n]_{ij}$$$
================================================================================
Finding distances: breadth first search
- Find the distance between "node 0" and "node 4"
step1. start at 0
 step2. find the nodes adjacent to 1.
Mark them as at distance 1.
Put them in a queue.
step2. find the nodes adjacent to 1.
Mark them as at distance 1.
Put them in a queue.
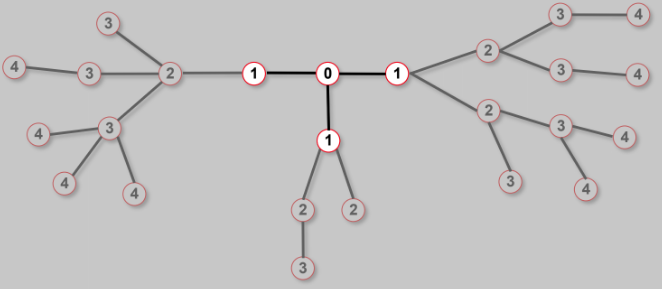 step3. Take the "first node" out of the queue.
Find the unmarked nodes adjacent to it in the graph.
Mark them with the label of 2.
Put them in the queue.
step3. Take the "first node" out of the queue.
Find the unmarked nodes adjacent to it in the graph.
Mark them with the label of 2.
Put them in the queue.
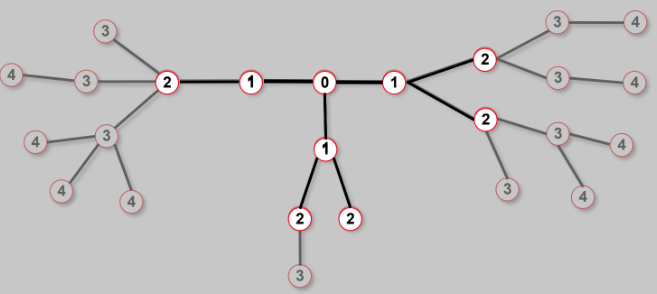 step4. repeat until you find "node 4" or until there are no more nodes in the queue
step5. the distance between 0 and 4 is the label of 4, or, if 4 does not have a label, it's infinity
step4. repeat until you find "node 4" or until there are no more nodes in the queue
step5. the distance between 0 and 4 is the label of 4, or, if 4 does not have a label, it's infinity
 ================================================================================
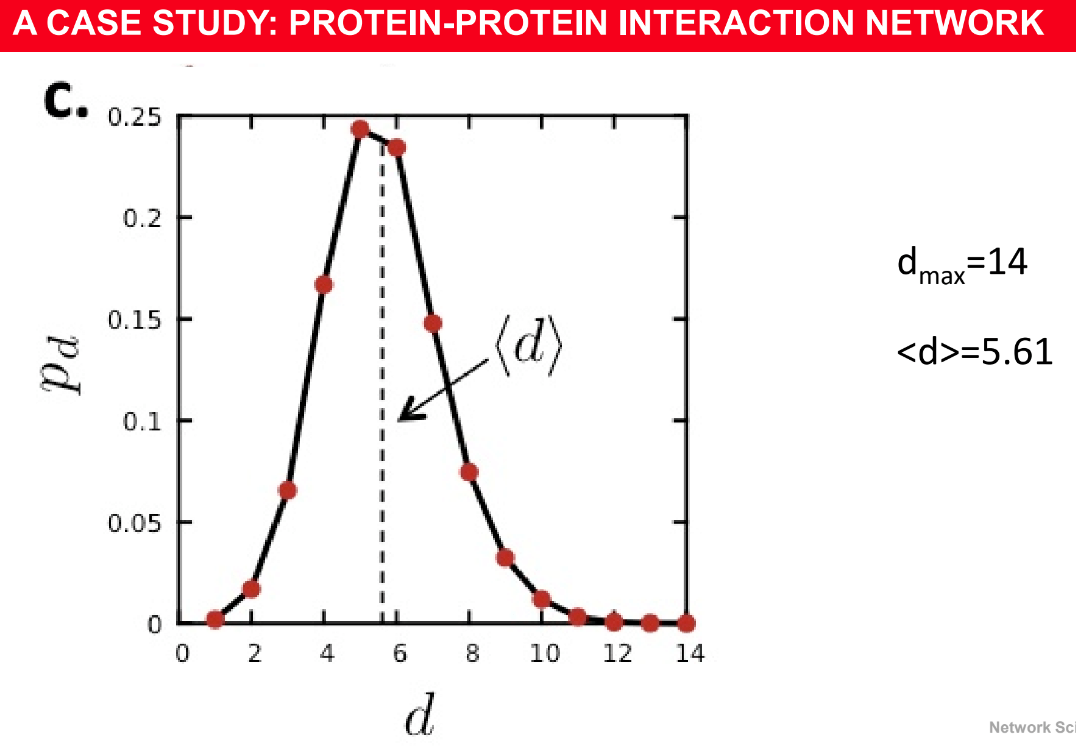
Network diameter and Average distance
Diameter: maximum distance ($$$d_{max}$$$) between any pair of nodes in the graph
Average path length/distance ($$$\left< d \right>$$$), for a connected graph:
$$$\left< d \right> \equiv \dfrac{1}{2L_{max}} \sum\limits_{i,j\ne 1} d_{ij}$$$
where, $$$d_{ij}$$$ is the distance from node i to node j
================================================================================
In "undirected graph", $$$d_{ij} = d_{ji}$$$
So, we only need to count them once
$$$\left< d \right> = \frac{1}{L_{max}} \sum\limits_{i,j>i}d_{ij}$$$
================================================================================
Pathology summary
================================================================================
Network diameter and Average distance
Diameter: maximum distance ($$$d_{max}$$$) between any pair of nodes in the graph
Average path length/distance ($$$\left< d \right>$$$), for a connected graph:
$$$\left< d \right> \equiv \dfrac{1}{2L_{max}} \sum\limits_{i,j\ne 1} d_{ij}$$$
where, $$$d_{ij}$$$ is the distance from node i to node j
================================================================================
In "undirected graph", $$$d_{ij} = d_{ji}$$$
So, we only need to count them once
$$$\left< d \right> = \frac{1}{L_{max}} \sum\limits_{i,j>i}d_{ij}$$$
================================================================================
Pathology summary
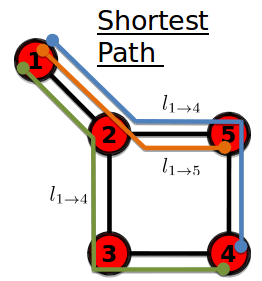 Shortest path of $$$l_{1 \rightarrow 4}$$$ = 3
Shortest path of $$$l_{1 \rightarrow 5}$$$ = 2
================================================================================
Diameter
Shortest path of $$$l_{1 \rightarrow 4}$$$ = 3
Shortest path of $$$l_{1 \rightarrow 5}$$$ = 2
================================================================================
Diameter
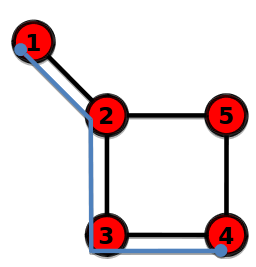 The longest shortest path in a graph
$$$l_{1 \rightarrow 4} = 3$$$
================================================================================
Average path length
The longest shortest path in a graph
$$$l_{1 \rightarrow 4} = 3$$$
================================================================================
Average path length
 ================================================================================
Cycle
================================================================================
Cycle
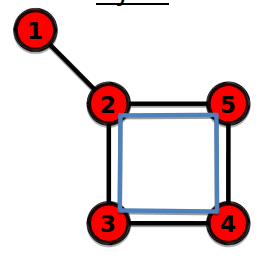 A path with the same start node and end node
================================================================================
Self-avoiding path
A path with the same start node and end node
================================================================================
Self-avoiding path
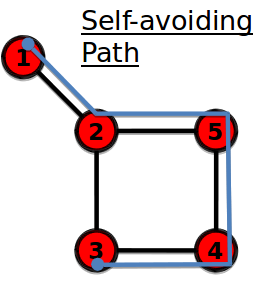 A path that does not intersect itself
================================================================================
Eulerian path
A path that does not intersect itself
================================================================================
Eulerian path
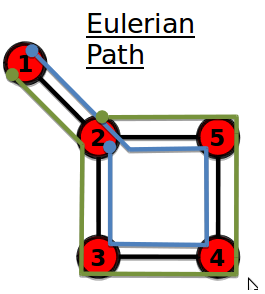 A path that traverses each link exactly once
================================================================================
Hamiltonian path
A path that traverses each link exactly once
================================================================================
Hamiltonian path
 A path that visits each node exactly once
================================================================================
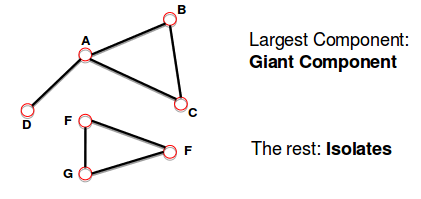
- Connected (undirected) graph:
- any two vertices can be joined by a path.
- A disconnected graph is made up by two or more connected components.
A path that visits each node exactly once
================================================================================
- Connected (undirected) graph:
- any two vertices can be joined by a path.
- A disconnected graph is made up by two or more connected components.
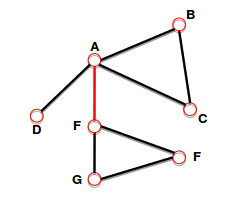
 Bridge: if you erase it, the graph becomes disconnected
================================================================================
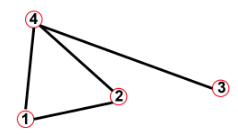
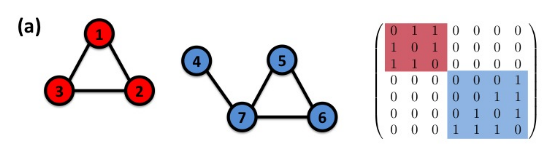
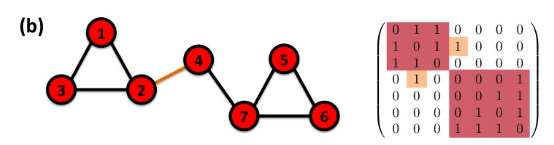
Connectivity of undirected graphs (adjacency matrix)
The adjacency matrix of a network with several components can be written in a block-diagonal form,
so that nonzero elements are confined to squares, with all other elements being zero:
Bridge: if you erase it, the graph becomes disconnected
================================================================================
Connectivity of undirected graphs (adjacency matrix)
The adjacency matrix of a network with several components can be written in a block-diagonal form,
so that nonzero elements are confined to squares, with all other elements being zero:
 ================================================================================
- Strongly connected directed graph:
- It has a path from "each node" to "every other node" and vice versa (e.g. AB path and BA path).
- Weakly connected directed graph:
- it is connected if we disregard the edge directions.
- Strongly connected components can be identified,
but not every node is part of a nontrivial strongly connected component.
================================================================================
- Strongly connected directed graph:
- It has a path from "each node" to "every other node" and vice versa (e.g. AB path and BA path).
- Weakly connected directed graph:
- it is connected if we disregard the edge directions.
- Strongly connected components can be identified,
but not every node is part of a nontrivial strongly connected component.
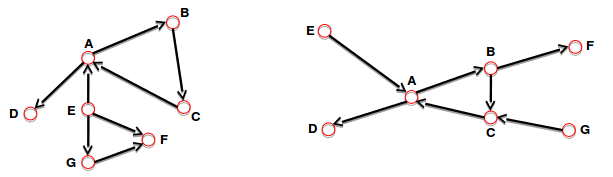 In-component: nodes that can reach the scc,
Out-component: nodes that can be reached from the scc.
================================================================================
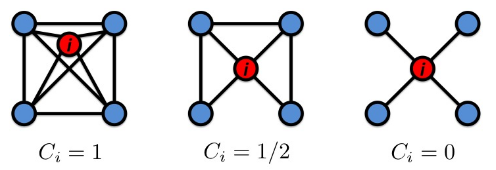
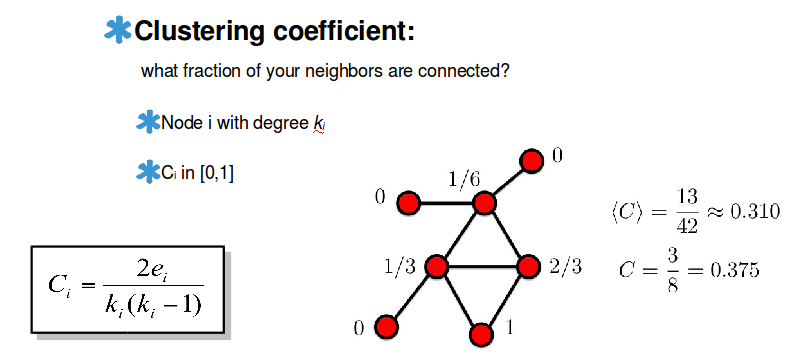
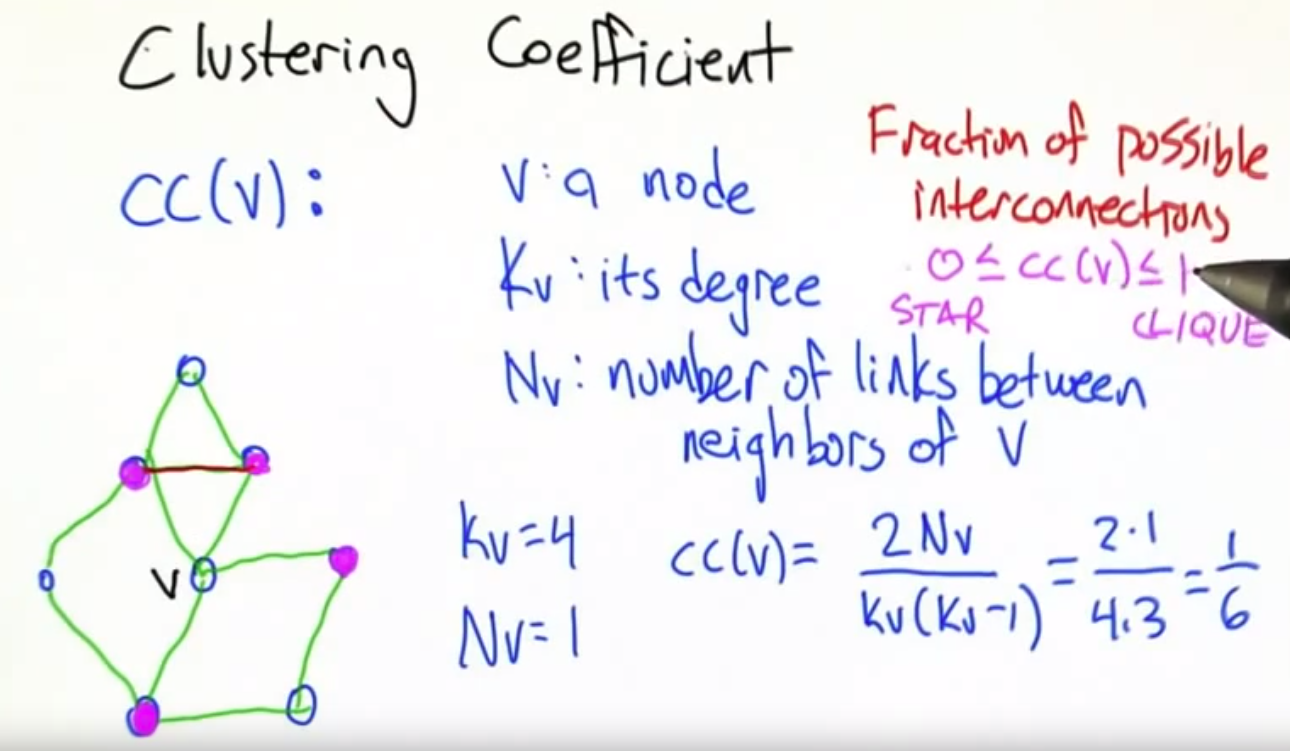
Clustering coefficient
$$$C_i$$$: clustering coefficient of node i with degree $$$k_i$$$
$$$0 \le C_i \le 1$$$
$$$C_i = \dfrac{2e_i}{k_i(k_i-1)}$$$
In-component: nodes that can reach the scc,
Out-component: nodes that can be reached from the scc.
================================================================================
Clustering coefficient
$$$C_i$$$: clustering coefficient of node i with degree $$$k_i$$$
$$$0 \le C_i \le 1$$$
$$$C_i = \dfrac{2e_i}{k_i(k_i-1)}$$$
 ================================================================================
Entire summary
- Degree distribution: $$$P(k)$$$
- Path length: $$$\left< d \right>$$$
- Clustering coefficient: $$$C_i = \dfrac{2e_i}{k_i(k_i-1)}$$$
- Undirected graph
================================================================================
Entire summary
- Degree distribution: $$$P(k)$$$
- Path length: $$$\left< d \right>$$$
- Clustering coefficient: $$$C_i = \dfrac{2e_i}{k_i(k_i-1)}$$$
- Undirected graph
 Adjacency matrix
$$$A_{ij}= \begin{bmatrix} 0&&1&&1&&0\\1&&0&&1&&1\\1&&1&&0&&0\\0&&1&&0&&0 \end{bmatrix}$$$
$$$A_{ii}=0$$$
$$$A_{ij}=A_{ji}$$$
$$$L=\frac{1}{2} \sum\limits_{i,j=1}^{N} A_{ij}$$$
$$$ \left< k \right> =\frac{2L}{N} $$$
- Directed graph
Adjacency matrix
$$$A_{ij}= \begin{bmatrix} 0&&1&&1&&0\\1&&0&&1&&1\\1&&1&&0&&0\\0&&1&&0&&0 \end{bmatrix}$$$
$$$A_{ii}=0$$$
$$$A_{ij}=A_{ji}$$$
$$$L=\frac{1}{2} \sum\limits_{i,j=1}^{N} A_{ij}$$$
$$$ \left< k \right> =\frac{2L}{N} $$$
- Directed graph
 Adjacency matrix
$$$A_{ij}= \begin{bmatrix} 0&&1&&0&&0\\0&&0&&1&&1\\1&&0&&0&&0\\0&&0&&0&&0 \end{bmatrix}$$$
$$$A_{ii}=0$$$
$$$A_{ij}\ne A_{ji}$$$
$$$L = \sum\limits_{i,j=1}^{N} A_{ij}$$$
$$$ \left< k \right> = \frac{L}{N} $$$
================================================================================
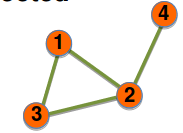
Undirected unweighted graph
Adjacency matrix
$$$A_{ij}= \begin{bmatrix} 0&&1&&0&&0\\0&&0&&1&&1\\1&&0&&0&&0\\0&&0&&0&&0 \end{bmatrix}$$$
$$$A_{ii}=0$$$
$$$A_{ij}\ne A_{ji}$$$
$$$L = \sum\limits_{i,j=1}^{N} A_{ij}$$$
$$$ \left< k \right> = \frac{L}{N} $$$
================================================================================
Undirected unweighted graph
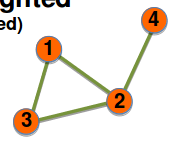
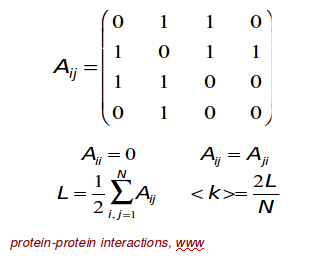 Undirected weighted graph
Undirected weighted graph
 ================================================================================
Self-interactions
================================================================================
Self-interactions
 ================================================================================
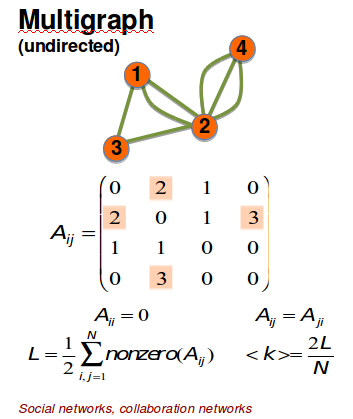
Multigraph
================================================================================
Multigraph
 ================================================================================
Complete graph (undirected)
================================================================================
Complete graph (undirected)
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================
 ================================================================================
================================================================================



































































