<![CDATA[
https://datascienceschool.net/view-notebook/0c66f1810445488baf19cac79305793b/
================================================================================
Constrained optimization
$$$x^{\ast} = \arg_x \min f(x) \;\; (x \in \mathbf{R}^N)$$$
* Equality constraint you should satisfy in solving above optimization problem
$$$g_j(x)=0 \;\; (j=1, \ldots, M)$$$
$$$g_1(x) = 0 \\
g_2(x) = 0 \\
\;\;\;\;\; \vdots \\
g_M(x) = 0$$$
================================================================================
Example of equality constrained optimization
* Objective function f
$$$f(x_1, x_2) = x_1^2 + x_2^2$$$
* Upsidedown 3D corn shape
* Equality constraint
$$$g(x_1, x_2) = x_1 + x_2 - 1 = 0$$$
* Green line
* Find $$$x_1^*, x_2^*$$$ values which make minimum y value
from on the line of green $$$g(x_1,x_2)$$$ line
]]>
<![CDATA[
================================================================================
Equality constrained optimization can be performed by using "Lagrange multipier"
* Objective function f(x)
* New objective function h(x,\lambda)
$$$h(x, \lambda) \\
= h(x_1, x_2, \ldots , x_N, \lambda_1, \ldots , \lambda_M) \\
= f(x) + \sum\limits_{j=1}^M [\lambda_j g_j(x)]$$$
* You multiply variable $$$\lambda$$$ by "equality constraint equation $$$g_j(x)$$$"
* M number of constraint functions $$$g_1(x),\cdots,g_M(x)$$$
M number of variables $$$\lambda_1,\cdots,\lambda_M$$$
* To find minimum or maximum location at x, you need to calculate derivative (gradient)=0
That becomes N+M number of conditions
Defferentiation f with respect to x
$$$\dfrac{\partial h}{\partial x_1}
= \dfrac{\partial f}{\partial x_1} + \sum_{j=1}^M \lambda_j\dfrac{\partial g_j}{\partial x_1} = 0 \\
\dfrac{\partial h}{\partial x_2}
= \dfrac{\partial f}{\partial x_2} + \sum_{j=1}^M \lambda_j\dfrac{\partial g_j}{\partial x_2} = 0 \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\
\dfrac{\partial h}{\partial x_N}
= \dfrac{\partial f}{\partial x_N} + \sum_{j=1}^M \lambda_j\dfrac{\partial g_j}{\partial x_N} = 0$$$
Defferentiation g with respect to $$$\lambda$$$
$$$\dfrac{\partial h}{\partial \lambda_1}
= g_1 = 0 \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\
\dfrac{\partial h}{\partial \lambda_M}
= g_M = 0 $$$
* Solve above $$$N+M$$$ simultaneous equations
* Find $$$N+M$$$ unknows; $$$x_1, x_2, \ldots, x_N, , \lambda_1, \ldots , \lambda_M$$$
* $$$x_1, x_2, \ldots, x_N$$$ are x values which minimies objective function
* Lagrange multiplier values of $$$\lambda_1, \ldots , \lambda_M$$$ can be thrown away for the solutions
================================================================================
* Example
* Objective function
$$$f(x_1,x_2)=x_1^2+x_2^2$$$
* Constraint function
$$$g(x_1,x_2)=x_1+x_2-1$$$
* New objective function by using Lagrange multipiler
$$$h(x_1,x_2,\lambda) \\
= f(x_1,x_2) + \lambda g(x_1,x_2) \\
= x_1^2 + x_2^2 + \lambda ( x_1 + x_2 - 1 )$$$
* Get gradient=0
Differentiation h wrt x
$$$\dfrac{\partial h}{\partial x_1} = 2{x_1} + \lambda = 0$$$
$$$\dfrac{\partial h}{\partial x_2} = 2{x_2} + \lambda = 0$$$
Differentiation h wrt $$$\lambda$$$
$$$\dfrac{\partial h}{\partial \lambda} = x_1 + x_2 - 1 = 0$$$
* Get solution of above simultaneous equations
$$$x_1=\dfrac{1}{2}$$$, $$$x_2 = \dfrac{1}{2}$$$, $$$\lambda = -1$$$
================================================================================
Solve equality constrained optimization problem by using SciPy
# Objective function $$$f(x_0,x_1)=x_0^2+x_1^2$$$
def f1array(x):
return x[0]**2+x[1]**2
# Equality constraint $$$g(x_0,x_1)=x_0+x_1-1$$$
def eq_constraint(x):
return x[0]+x[1]-1
sp.optimize.fmin_slsqp(f1array,np.array([1,1]),eqcons=[eq_constraint])
# Optimization terminated successfully. (Exit mode 0)
# Current function value: 0.5000000000000002
# Iterations: 2
# Function evaluations: 8
# Gradient evaluations: 2
# array([0.5, 0.5])
================================================================================
Meaning of Lagrange multipier $$$\lambda$$$
with scope:optimization problem
solution1=f_x
solution2=f_x,equality_constraint
if solution1!=solution2:
lambda!=0
================================================================================
Inequality constrained optimization
* Objective function
$$$x^{\ast} = \text{arg}_x \min f(x) \;\; (x \in \mathbf{R}^N)$$$
* Inequality constraint function
$$$g_j(x) \leq 0 \;\; (j=1, \ldots, M)$$$
If you have inequality constraint $$$g_j(x) \ge 0$$$, multiply -1 to make $$$g_j(x) \le 0$$$
================================================================================
* New objective function
$$$h(x, \lambda) = f(x) + \sum_{j=1}^M \lambda_j g_j(x)$$$
================================================================================
* 3 conditions (KKT condition) for solution to exist
1. Differentiation h wrt all independent x values should be 0
with respect to all independant variables $$$x_1,\cdots,x_N$$$
$$$\dfrac{\partial h(x, \lambda)}{\partial x_1} = 0$$$
$$$\;\;\;\;\;\;\;\; \vdots$$$
$$$\dfrac{\partial h(x, \lambda)}{\partial x_N} = 0$$$
2.
$$$\lambda_1 \times g_1(x) = \lambda_1 \times \dfrac{\partial h(x,\lambda)}{\partial \lambda_1} = 0$$$
$$$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots$$$
$$$\lambda_M \times g_M(x) = \lambda_M \times \dfrac{\partial h(x,\lambda)}{\partial \lambda_M} = 0$$$
3.
Lagrange multipliers ($$$\lambda_j$$$) should be $$$\ge$$$ 0
================================================================================
* Example
* Objective function
$$$f(x_1,x_2)=x_1^2+x_2^2$$$
* Inequality constraint case 1:
$$$g(x_1,x_2)=x_1+x_2-1 \le 0$$$
* Inequality constraint case 2:
$$$g(x_1,x_2)=-x_1-x_2+1 \le 0$$$
================================================================================
]]>
<![CDATA[
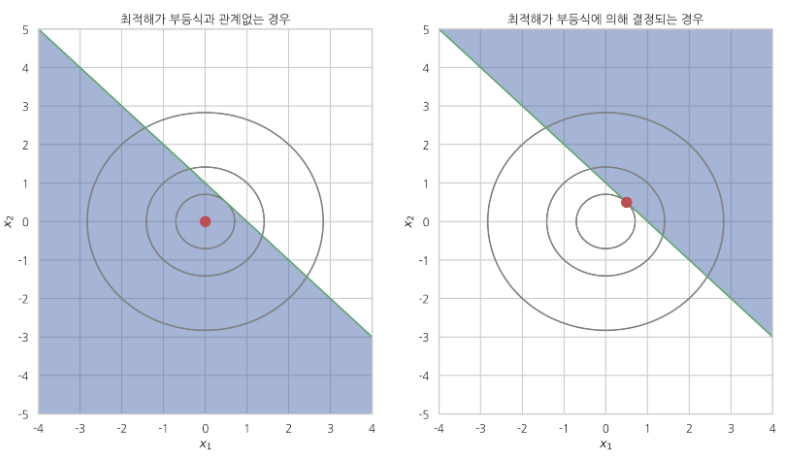* Dark areas: inequality constraints
* Red point: solution $$$x_1, x_2$$$
* Case1: constraint is actually meaningless
* Case2: constraint affects solution
================================================================================
* Example of inequality constrained optimization
* Problem: $$$\arg_{x}\min (x_1-4)^2 + (x_2-2)^2$$$
* 4 constraints:
- $$$g_1(x)=x_1+x_2-1 \le 0$$$
- $$$g_2(x)=-x_1+x_2-1 \le 0$$$
- $$$g_3(x)=-x_1-x_2-1 \le 0$$$
- $$$g_4(x)=x_1-x_2-1 \le 0$$$
* 4 constraints in one inequality equation
$$$g(x) \\
= \left\vert\, x_1 \right\vert + \left\vert\, x_2 \right\vert - 1 \\
= \sum_{i=1}^{2} \left\vert\, x_i \right\vert - 1 \leq 0$$$
================================================================================
]]>
<![CDATA[
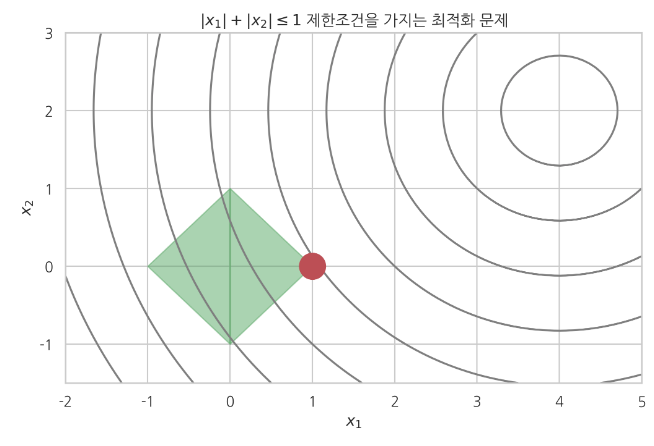* Circles: objective function
* Green rectangle area: inequality constraints
* Red point: solution $$$x_1,x_2$$$
================================================================================
* Solve inequality constrained optimization problem by using SciPy
# Objective function
def f2(x):
return np.sqrt((x[0]-4)**2+(x[1]-2)**2)
# c k: Constraint condition constant
k=1
def ieq_constraint(x):
return np.atleast_1d(k-np.sum(np.abs(x)))
sp.optimize.fmin_slsqp(f2,np.array([0,0]),ieqcons=[ieq_constraint])
# Optimization terminated successfully. (Exit mode 0)
# Current function value: 3.6055512804550336
# Iterations: 11
# Function evaluations: 77
# Gradient evaluations: 11
# array([9.99999982e-01, 1.79954011e-08])
]]>