- Suppose 2 random variables X and Y
- Suppose X and Y can have categorical values from 1 to 6
- You need to consider
probability distribution of random variable X,
probability distribution of random variable Y,
probability distribution of random variable pair of X,Y
================================================================================
Probability distribution of random variables X and Y can be expressed by probability mass functions
$$$P_X(x)$$$, $$$P_Y(y)$$$
$$$P_X(x)$$$: probability mass function of random variable X
$$$P_Y(x)$$$: probability mass function of random variable Y
================================================================================
$$$P_X(x=1) or P_X(1)$$$: means probability of 1 occuring from random variable X
================================================================================
Joint probability mass function of X and Y: $$$P_{XY}(x,y)$$$
$$$P_{XY}(x=2,y=3)$$$: means
- probability of event {x=2,y=3} occuring
================================================================================
Marginal probability mass function
It's probability distribution function wrt one random variable from joint probability mass function
================================================================================
How to calculate marginal probability mass function
$$$P_X(x)=\sum\limits_{y_i} P_{XY}(x,y_i)$$$
$$$P_Y(y)=\sum\limits_{x_i} P_{XY}(x_i,y)$$$
$$$P_X(A) \\
= P_{XY}(A,A) + P_{XY}(A,B) + P_{XY}(A,C) + P_{XY}(A,D) + P_{XY}(A,E) + P_{XY}(A,F) \\
= 0.02$$$
================================================================================
Conditional probability mass function
When y is already occurred and fixed,
$$$P_{X \mid Y}(x \mid y) = \dfrac{P_{XY}(x, y)}{P_{Y}(y)}$$$
When x is already occurred and fixed,
$$$P_{Y \mid X}(y \mid x) = \dfrac{P_{XY}(x, y)}{P_{X}(x)}$$$
For continuous probability distribution,
you can define the probability value from simple event like discrete probability distribution
So, you first define cumulitive probability distribution function,
and you perform differentiation on it, and you can define (or obtain) probability density function
================================================================================
You define "joint cumulitive probability distribution function $$$F_{XY}(x,y)$$$
wrt 2 continuous random variable X and Y" as follow:
$$$F_{XY}(x, y) = P(\{ X < x \} \cap \{ Y < y \}) = P(\{X < x, Y < y\})$$$
================================================================================
joint cumulitive probability distribution function $$$F_{XY}(x,y)$$$ has following characteristics.
- $$$F_{XY}(\infty,\infty)=1$$$
- $$$F_{XY}(-\infty, y)=F_{XY}(x,-\infty)=0$$$
================================================================================
If one of independent variable x and y has infinite value,
it becomes marginal cumulative probability distribution
$$$F_X(x)=F_{XY}(x,\infty)$$$
$$$F_Y(y)=F_{XY}(\infty,y)$$$
================================================================================
How to get joint probability density function from cumulitive probability distribution function
You can use partial differentiation because you have 2 independent random variables
$$$f_{XY} = \dfrac{\partial^2 F_{XY}(x,y)}{\partial x \partial y}$$$
================================================================================
If you perform integration on joint probability density function using specific interval,
it becomes probability value of that interval
$$$\int_{x_1}^{x_2} \int_{y_1}^{y_2} f_{XY}(x,y)dxdy = P\big(\{ x_1 \leq X \leq x_2, \; y_1 \leq Y \leq y_2 \}\big)$$$
================================================================================
If you perform integration wrt all variables like both x and y
using interval of $$$-\infty$$$ to $$$\infty$$$, it becomes 1
================================================================================
Joint probability density function in 2D
 Joint probability density function in 3D
Joint probability density function in 3D
 ================================================================================
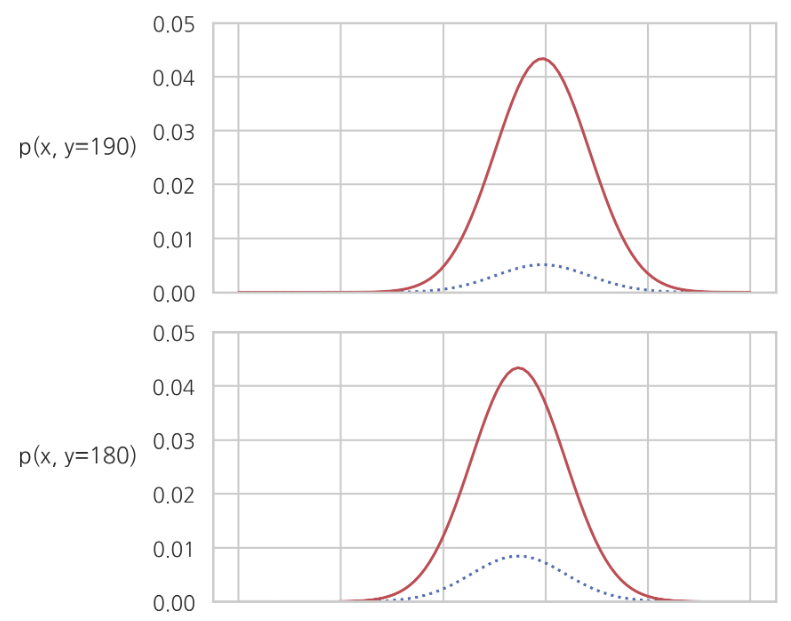
If y is fixed, cut view in 3D
================================================================================
If y is fixed, cut view in 3D

 ================================================================================
Marginal probability density function
You perform weighted averge on joint probability density function wrt one variable
In conclusion, you perform integration on joint probability density function wrt one random variable
$$$f_X(x) = \int_{-\infty}^{\infty} f_{XY}(x,y)dy$$$
$$$f_Y(y) = \int_{-\infty}^{\infty} f_{XY}(x,y)dx$$$
================================================================================
2 marginal probability density functions from one joint probability density function
================================================================================
Marginal probability density function
You perform weighted averge on joint probability density function wrt one variable
In conclusion, you perform integration on joint probability density function wrt one random variable
$$$f_X(x) = \int_{-\infty}^{\infty} f_{XY}(x,y)dy$$$
$$$f_Y(y) = \int_{-\infty}^{\infty} f_{XY}(x,y)dx$$$
================================================================================
2 marginal probability density functions from one joint probability density function
 ================================================================================
Conditional probability density function
One random variable from multi random variables had already occurred as specific value,
it becomes as following.
$$$f_{X \mid Y}(x \mid y) = \dfrac{f_{XY}(x, y)}{f_{Y}(y)}$$$
$$$f_{Y \mid X}(y \mid x) = \dfrac{f_{XY}(x, y)}{f_{X}(x)}$$$
Since already-occurred-random-variable is fixed one, it can be considered as paramter than variable
For example, $$$f_{X|Y}(x|y)$$$ is function wrt x because $$$y$$$ is fixed.
================================================================================
================================================================================
Conditional probability density function
One random variable from multi random variables had already occurred as specific value,
it becomes as following.
$$$f_{X \mid Y}(x \mid y) = \dfrac{f_{XY}(x, y)}{f_{Y}(y)}$$$
$$$f_{Y \mid X}(y \mid x) = \dfrac{f_{XY}(x, y)}{f_{X}(x)}$$$
Since already-occurred-random-variable is fixed one, it can be considered as paramter than variable
For example, $$$f_{X|Y}(x|y)$$$ is function wrt x because $$$y$$$ is fixed.
================================================================================

 ================================================================================
================================================================================







