================================================================================
Covariance and correlation coefficient are the numbers
which represent correlation between multivarite random variables
================================================================================
Sample covariance
$$$s_{xy}=\frac{1}{N} \sum\limits_{i=1}^{N} (x_i-\bar{x})(y_i-\bar{y})$$$
$$$x_i, y_i$$$: ith x and y samples
$$$\bar{x}, \bar{y}$$$: sample's average of x and y
================================================================================
Like sample variance, sample covariance represents how far sample is located from the mean value
================================================================================
Sample covariance shows "size" and "direction"
which represents how samples are distributed around the mean value.
Size of distribution can be revealed by "variance" without using "covariance"
So, you need a way which you can use to see "direction" of sample.
To do that, you can use "sample correlation coefficient"
================================================================================
$$$r_{xy}=\frac{s_{xy}}{\sqrt{s_x^2\cdot s_y^2}}$$$
$$$s_{xy}$$$: sample covariance
$$$\sqrt{s_x^2}$$$: std of x
$$$\sqrt{s_y^2}$$$: std of y
================================================================================
There are other correlation coefficients which are differently defined
such as Pearson correlation coefficient.
================================================================================
Covariance of 2 random variables X and Y is defined using E
$$$Cov[X,Y]=E[(X-E[X])(Y-E[Y])]$$$
================================================================================
Correlation coefficient of 2 random variables is defined as following
$$$\rho[X,Y]=\dfrac{Cov[X,Y]}{\sqrt{Var[X]\cdot Var[Y]}}$$$
$$$-1 \le \rho\le 1$$$
================================================================================
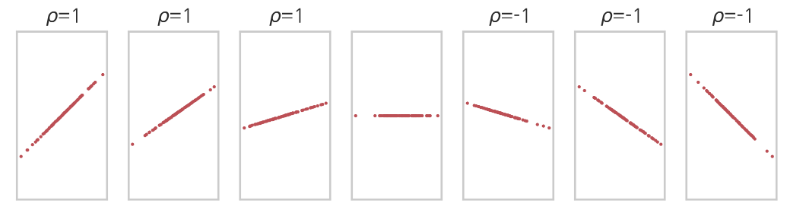
$$$\rho=1$$$: full liearly correlation relationship
$$$\rho=0$$$: none correlation relationship
$$$\rho=-1$$$: full opposed liearly correlation relationship
 ================================================================================
Slope of plot has no effect to correlation coefficient.
================================================================================
Slope of plot has no effect to correlation coefficient.
 ================================================================================
Sample covariance of multivariate random variables
- M-dimensional random variable $$$x=\begin{bmatrix} x_1\\x_2\\\vdots\\x_M \end{bmatrix}$$$
$$$x_1, x_2, ...$$$: random variables which return scalar values
- Suppose you extract N number of sample, creating $$$N\times M$$$ feature matrix X
$$$X =
\begin{bmatrix}
x_{1, 1} & x_{1, 2} & \cdots & x_{1, M} \\
x_{2, 1} & x_{2, 2} & \cdots & x_{2, M} \\
\vdots & \vdots & \ddots & \vdots \\
x_{N, 1} & x_{N, 2} & \cdots & x_{N, M} \\
\end{bmatrix}$$$
================================================================================
$$$c_1 =
\begin{bmatrix}
x_{1, 1}\\
x_{2, 1}\\
\vdots \\
x_{N, 1}
\end{bmatrix}$$$
$$$x_{1, 1},x_{2, 1},\cdots,x_{N, 1}$$$: sample data from random variable $$$x_1$$$
================================================================================
$$$\text{E}[x_j] = \bar{x}_j = \dfrac{1}{N} \sum_{i=1}^N x_{i,j}
= \dfrac{1}{N} \mathbf{1}_N^T c_j = \dfrac{1}{N} c_j^T \mathbf{1}_N$$$
$$$E[x_j]$$$: expectation value of each random variable
$$$1_N$$$: N-dim 1 vector
================================================================================
Sample covariance of multivariate random variables
- M-dimensional random variable $$$x=\begin{bmatrix} x_1\\x_2\\\vdots\\x_M \end{bmatrix}$$$
$$$x_1, x_2, ...$$$: random variables which return scalar values
- Suppose you extract N number of sample, creating $$$N\times M$$$ feature matrix X
$$$X =
\begin{bmatrix}
x_{1, 1} & x_{1, 2} & \cdots & x_{1, M} \\
x_{2, 1} & x_{2, 2} & \cdots & x_{2, M} \\
\vdots & \vdots & \ddots & \vdots \\
x_{N, 1} & x_{N, 2} & \cdots & x_{N, M} \\
\end{bmatrix}$$$
================================================================================
$$$c_1 =
\begin{bmatrix}
x_{1, 1}\\
x_{2, 1}\\
\vdots \\
x_{N, 1}
\end{bmatrix}$$$
$$$x_{1, 1},x_{2, 1},\cdots,x_{N, 1}$$$: sample data from random variable $$$x_1$$$
================================================================================
$$$\text{E}[x_j] = \bar{x}_j = \dfrac{1}{N} \sum_{i=1}^N x_{i,j}
= \dfrac{1}{N} \mathbf{1}_N^T c_j = \dfrac{1}{N} c_j^T \mathbf{1}_N$$$
$$$E[x_j]$$$: expectation value of each random variable
$$$1_N$$$: N-dim 1 vector

