https://datascienceschool.net/view-notebook/c2934b8a2f9140e4b8364b266b1aa0d8/
================================================================================
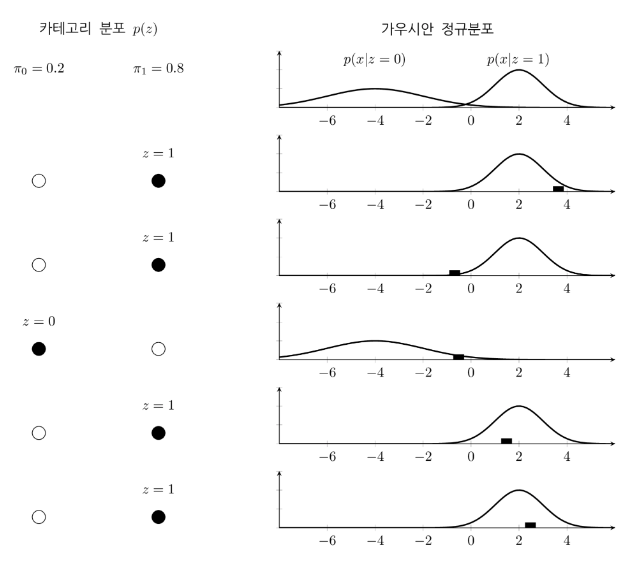
* Suppose categorical random variable Z.
* Probability distribution function of Z is $$$p(z=k)=\pi_k$$$
* Suppose random variable X which outputs real numbers.
* Suppose when sample k of random variable Z varies,
expectation value $$$\mu_k$$$ and variance $$$\Sigma_k$$$ of random variable X vary
* $$$p(x|z) = \mathcal{N}(x|\mu_k,\Sigma_k)$$$
* You can merge above ones.
$$$p(x)$$$
$$$= \sum\limits_Z p(z)p(x\mid z) $$$
$$$= \sum\limits_{k=1}^{K} \pi_k \mathcal{N}(x \mid \mu_k, \Sigma_k)$$$
================================================================================
output_from_random_variable_Z=K_class_categorical_random_variable_Z(result_from_trial)
output_from_random_variable_X=random_variable_X_which_outputs_real_number(
result_from_trial,output_from_random_variable_Z)
mean,var=mean_var(output_from_random_variable_X)
output_from_random_variable_Z varies --> mean,var vary:
- X is composed of multiple Gaussian normal distributions
- X is Gaussian mixture model
================================================================================
with scope:Gaussian_mixture_model
you can't know output_from_random_variable_Z
Model which contains "latent random variable" is called "latent variable model"
with scope:Mixture_model
categorical_value=latent_random_variable(result_from_trial)
with scope:Other_models
float_value=latent_random_variable(result_from_trial)
================================================================================
Bernoulli Gaussian mixture mdoel: category is 2
output_from_bernoulli_random_variable=bernoulli_random_variable(result_from_trial)
# output_from_bernoulli_random_variable={category1,category2}
output_from_Gaussian_normal_distribution=Gaussian_normal_distribution(
result_from_trial,output_from_bernoulli_random_variable)
output_from_bernoulli_random_variable_case1
output_from_Gaussian_normal_distribution_case1
output_from_bernoulli_random_variable_case2
output_from_Gaussian_normal_distribution_case2
output_from_bernoulli_random_variable_case3
output_from_Gaussian_normal_distribution_case3
output_from_bernoulli_random_variable_case4
output_from_Gaussian_normal_distribution_case4
output_from_bernoulli_random_variable_case5
output_from_Gaussian_normal_distribution_case5
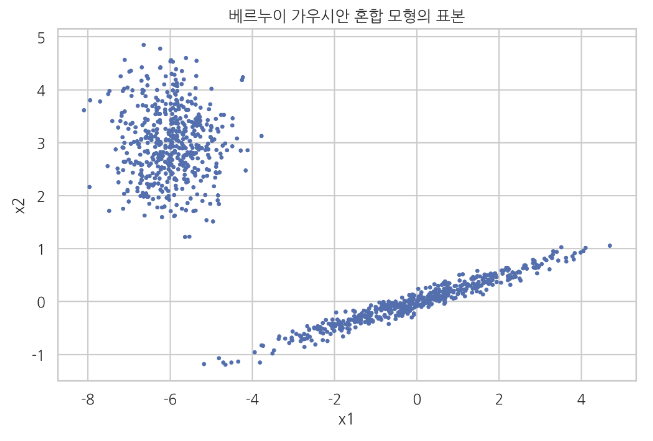
 ================================================================================
Bernoulli (2 categories) + Gaussian (2D) mixture model
* Code
from numpy.random import randn
n_samples=500
# c mu1: first mean for 2 models
mu1=np.array([0,0])
# c mu2: second mean for 2 models
mu2=np.array([-6,3])
sigma1=np.array([[0.,-0.1],[1.7,.4]])
sigma2=np.eye(2)
np.random.seed(0)
X=np.r_[1.0*np.dot(randn(n_samples,2),sigma1)+mu1,
0.7*np.dot(randn(n_samples,2),sigma2)+mu2]
plt.scatter(X[:,0],X[:,1],s=5)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Samples of Bernoulli-Gaussian mixture model")
plt.show()
================================================================================
Bernoulli (2 categories) + Gaussian (2D) mixture model
* Code
from numpy.random import randn
n_samples=500
# c mu1: first mean for 2 models
mu1=np.array([0,0])
# c mu2: second mean for 2 models
mu2=np.array([-6,3])
sigma1=np.array([[0.,-0.1],[1.7,.4]])
sigma2=np.eye(2)
np.random.seed(0)
X=np.r_[1.0*np.dot(randn(n_samples,2),sigma1)+mu1,
0.7*np.dot(randn(n_samples,2),sigma2)+mu2]
plt.scatter(X[:,0],X[:,1],s=5)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Samples of Bernoulli-Gaussian mixture model")
plt.show()
 ================================================================================
How to inference parameters of Gaussian mixture model
estimated_paramters=estimate_parameters_of_Gaussian_mixture_model()
print("estimated_paramters",estimated_paramters)
# PDF of categorical distribution
# PDF of Gaussian normal distribution at category1
# PDF of Gaussian normal distribution at category2
# PDF of Gaussian normal distribution at category3
Gaussian_mixture_model has complicated shape to find its PDF via linear algebra methods
================================================================================
Probability distribution of random variable X which has N number of data is as follow
$$$p(x)$$$
$$$=\prod\limits_{i=1}^N p(x_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{z_i} p(x_i,z_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{z_i} p(z_i)p(x_i\mid z_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{k=1}^{K} \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)$$$
* You can use log
$$$\log p(x) = \sum\limits_{i=1}^N \log \left( \sum\limits_{k=1}^{K} \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k) \right)$$$
* Both equations are the ones where you can't easily find the parameters
which satisfy derivatives=0
================================================================================
* If you know which "category $$$z_i$$$" "data $$$x_i$$$" is involved in,
you can collect "all data $$$x_i$$$" which are involved in same "category $$$z_i$$$"
Then, you can find "categorical probability distribution $$$\pi_k$$$"
and you can find parameters "$$$\mu_k$$$" and "$$$\Sigma_k$$$" of "Gaussian normal distribution"
* However, you can't know "category $$$z_i$$$" which "data $$$x_i$$$" has.
So, you should find $$$\pi_k, \mu_k, \Sigma_k$$$ which maximize p(x)
by using non-linear optimization
================================================================================
* In network graphical probabilistic model perspective,
Gaussian mixture model is simple model where random varialbe $$$Z_i$$$ affects random variable $$$X_i$$$
================================================================================
How to inference parameters of Gaussian mixture model
estimated_paramters=estimate_parameters_of_Gaussian_mixture_model()
print("estimated_paramters",estimated_paramters)
# PDF of categorical distribution
# PDF of Gaussian normal distribution at category1
# PDF of Gaussian normal distribution at category2
# PDF of Gaussian normal distribution at category3
Gaussian_mixture_model has complicated shape to find its PDF via linear algebra methods
================================================================================
Probability distribution of random variable X which has N number of data is as follow
$$$p(x)$$$
$$$=\prod\limits_{i=1}^N p(x_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{z_i} p(x_i,z_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{z_i} p(z_i)p(x_i\mid z_i)$$$
$$$=\prod\limits_{i=1}^N \sum\limits_{k=1}^{K} \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)$$$
* You can use log
$$$\log p(x) = \sum\limits_{i=1}^N \log \left( \sum\limits_{k=1}^{K} \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k) \right)$$$
* Both equations are the ones where you can't easily find the parameters
which satisfy derivatives=0
================================================================================
* If you know which "category $$$z_i$$$" "data $$$x_i$$$" is involved in,
you can collect "all data $$$x_i$$$" which are involved in same "category $$$z_i$$$"
Then, you can find "categorical probability distribution $$$\pi_k$$$"
and you can find parameters "$$$\mu_k$$$" and "$$$\Sigma_k$$$" of "Gaussian normal distribution"
* However, you can't know "category $$$z_i$$$" which "data $$$x_i$$$" has.
So, you should find $$$\pi_k, \mu_k, \Sigma_k$$$ which maximize p(x)
by using non-linear optimization
================================================================================
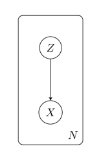
* In network graphical probabilistic model perspective,
Gaussian mixture model is simple model where random varialbe $$$Z_i$$$ affects random variable $$$X_i$$$
 * But, $$$Z_i$$$ affects $$$X_i$$$ sequentially from 1 to N
So, you should express like this
* But, $$$Z_i$$$ affects $$$X_i$$$ sequentially from 1 to N
So, you should express like this
 * Above graph can be expressed as following panel model
* Above graph can be expressed as following panel model
 ================================================================================
EM (Expectation-Maximization)
* When you inference "parameters" of "mixture model",
"conditional probability $$$p(z|x)$$$" is important,
which shows that data x is involved in which category z
* "Conditional probability $$$p(z|x)$$$" which is used for this case is called "responsibility"
* Responsibility $$$\pi_{ik}$$$ is written as follow
$$$\pi_{ik} \\
=p(z_i=k\mid x_i) \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{p(x_i)} \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(x_i,z_i=k)} \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(z_i=k)p(x_i\mid z_i=k)}$$$
* Responsibility $$$\pi_{ik}$$$ for Gaussian mixture model is written as follwo
$$$\pi_{ik} = \dfrac{\pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)}{\sum\limits_{k=1}^K \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)}$$$
================================================================================
* Above equation inferences responsibility $$$\pi_{ik}$$$ from parameters $$$\pi_k,\mu_k,\Sigma_k$$$
$$$(\pi_k, \mu_k, \Sigma_k)$$$ --inference--> $$$\pi_{ik}$$$
* $$$\pi_{ik}$$$: probability of that "ith data $$$x_i$$$" is created from "category k"
================================================================================
* Now, you will maximize log-joint probability distribution function
* First, you perform differentiation on "log-joint probability distribution function"
wrt $$$\mu_k$$$ to create equation
$$$0 = - \sum\limits_{i=1}^N \dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(z_i=k)p(x_i\mid z_i=k)} \Sigma_k (x_i - \mu_k )$$$
================================================================================
* You will simplify it
$$$\sum\limits_{i=1}^N \pi_{ik} (x_i - \mu_k ) = 0 $$$
$$$\mu_k = \dfrac{1}{N_k} \sum\limits_{i=1}^N \pi_{ik} x_i$$$
================================================================================
From above equation, you can know
$$$N_k = \sum_{i=1}^N \pi_{ik}$$$
* $$$N_k$$$: almost number of data which is involved in kth category
* $$$\mu_k$$$: almost sample mean value of data which is involved in kth category
================================================================================
Secondly, you perform differentiation on "log-joint probability distribution function" wrt $$$\Sigma_k$$$
and find parameter $$$\Sigma_k$$$ which maximizes differentiation
$$$\Sigma_k = \dfrac{1}{N_k} \sum_{i=1}^N \pi_{ik} (x_i-\mu_k)(x_i-\mu_k)^T$$$
================================================================================
Lastly, you perform differentiation on "log-joint probability distribution function" wrt $$$\pi_k$$$
and find parameter $$$\pi_k$$$ which maximizes differentiation
* Due to constraints which parameter of categorical random variable has,
you need to add Lagrange multiplier
$$$\log p(x) + \lambda \left(\sum_{k=1}^K \pi_k - 1 \right)$$$
* Then, you perform differentiation of above equation wrt $$$\pi_k$$$
and find value $$$\pi_k$$$ which satisfies derivatives=0
$$$\pi_k = \dfrac{N_k}{N}$$$
================================================================================
* Above 3 equations calculate parameters from "responsibility"
$$$\pi_{ik}$$$ --is used to calculate--> $$$(\pi_k, \mu_k, \Sigma_k )$$$
================================================================================
* Originally, you had to estimate parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$ and responsibility $$$\pi_{ik}$$$
* But if you already know responsibility $$$\pi_{ik}$$$,
equation becomes easy to find parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$
* So, you can use iterative method called EM to estimate parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$
* EM method inferences "parameter" and "responsibility" in turn with increasing precision of estimation
================================================================================
* E step
* You assume "parameters" you know are precise.
So, you "inference responsibility" which represents data is involved in which category
by using assumed parameters
$$$(\pi_k,\mu_k,\Sigma_k)$$$ --are used to inference--> $$$\pi_{ik}$$$
================================================================================
* M step
* You assume "responsibility" you know is precise
So, you inference "parameters of Gaussian mixture model" by using assumed responsibility
$$$\pi_{ik}$$$ --is used to inference--> $$$(\pi_k,\mu_k,\Sigma_k)$$$
================================================================================
* If you iterate above EM, you can make parameter and responsibility better gradually
================================================================================
* K-means clustering $$$\subset$$$ EM
If you can know "responsibility" of each data,
you can find maximal "responsibility" in which each data is involved
It means that you can perform "clustering"
$$$k_i = \arg_k\max \pi_{ik}$$$
K-means clustering is special case of EM algorithm
================================================================================
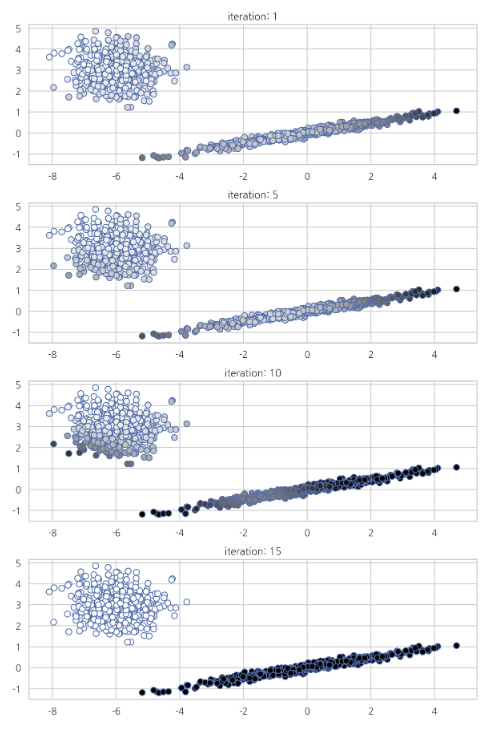
* GaussianMixture from Scikit-Learn
from sklearn.mixture import GaussianMixture
from sklearn.utils.testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
def plot_gaussianmixture(n):
# c model: GaussianMixture
model=GaussianMixture(
n_components=2,init_params='random',random_state=0,tol=1e-9,max_iter=n)
with ignore_warnings(category=ConvergenceWarning):
model.fit(X)
pi=model.predict_proba(X)
plt.scatter(X[:,0],X[:,1],s=50,linewidth=1,edgecolors="b",cmap=plt.cm.binary,c=pi[:,0])
plt.title("iteration:{}".format(n))
plt.figure(figsize=(8, 12))
plt.subplot(411)
plot_gaussianmixture(1)
plt.subplot(412)
plot_gaussianmixture(5)
plt.subplot(413)
plot_gaussianmixture(10)
plt.subplot(414)
plot_gaussianmixture(15)
plt.tight_layout()
plt.show()
================================================================================
EM (Expectation-Maximization)
* When you inference "parameters" of "mixture model",
"conditional probability $$$p(z|x)$$$" is important,
which shows that data x is involved in which category z
* "Conditional probability $$$p(z|x)$$$" which is used for this case is called "responsibility"
* Responsibility $$$\pi_{ik}$$$ is written as follow
$$$\pi_{ik} \\
=p(z_i=k\mid x_i) \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{p(x_i)} \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(x_i,z_i=k)} \\
=\dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(z_i=k)p(x_i\mid z_i=k)}$$$
* Responsibility $$$\pi_{ik}$$$ for Gaussian mixture model is written as follwo
$$$\pi_{ik} = \dfrac{\pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)}{\sum\limits_{k=1}^K \pi_k \mathcal{N}(x_i\mid \mu_k, \Sigma_k)}$$$
================================================================================
* Above equation inferences responsibility $$$\pi_{ik}$$$ from parameters $$$\pi_k,\mu_k,\Sigma_k$$$
$$$(\pi_k, \mu_k, \Sigma_k)$$$ --inference--> $$$\pi_{ik}$$$
* $$$\pi_{ik}$$$: probability of that "ith data $$$x_i$$$" is created from "category k"
================================================================================
* Now, you will maximize log-joint probability distribution function
* First, you perform differentiation on "log-joint probability distribution function"
wrt $$$\mu_k$$$ to create equation
$$$0 = - \sum\limits_{i=1}^N \dfrac{p(z_i=k)p(x_i\mid z_i=k)}{\sum\limits_{k=1}^K p(z_i=k)p(x_i\mid z_i=k)} \Sigma_k (x_i - \mu_k )$$$
================================================================================
* You will simplify it
$$$\sum\limits_{i=1}^N \pi_{ik} (x_i - \mu_k ) = 0 $$$
$$$\mu_k = \dfrac{1}{N_k} \sum\limits_{i=1}^N \pi_{ik} x_i$$$
================================================================================
From above equation, you can know
$$$N_k = \sum_{i=1}^N \pi_{ik}$$$
* $$$N_k$$$: almost number of data which is involved in kth category
* $$$\mu_k$$$: almost sample mean value of data which is involved in kth category
================================================================================
Secondly, you perform differentiation on "log-joint probability distribution function" wrt $$$\Sigma_k$$$
and find parameter $$$\Sigma_k$$$ which maximizes differentiation
$$$\Sigma_k = \dfrac{1}{N_k} \sum_{i=1}^N \pi_{ik} (x_i-\mu_k)(x_i-\mu_k)^T$$$
================================================================================
Lastly, you perform differentiation on "log-joint probability distribution function" wrt $$$\pi_k$$$
and find parameter $$$\pi_k$$$ which maximizes differentiation
* Due to constraints which parameter of categorical random variable has,
you need to add Lagrange multiplier
$$$\log p(x) + \lambda \left(\sum_{k=1}^K \pi_k - 1 \right)$$$
* Then, you perform differentiation of above equation wrt $$$\pi_k$$$
and find value $$$\pi_k$$$ which satisfies derivatives=0
$$$\pi_k = \dfrac{N_k}{N}$$$
================================================================================
* Above 3 equations calculate parameters from "responsibility"
$$$\pi_{ik}$$$ --is used to calculate--> $$$(\pi_k, \mu_k, \Sigma_k )$$$
================================================================================
* Originally, you had to estimate parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$ and responsibility $$$\pi_{ik}$$$
* But if you already know responsibility $$$\pi_{ik}$$$,
equation becomes easy to find parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$
* So, you can use iterative method called EM to estimate parameters $$$(\pi_k, \mu_k, \Sigma_k )$$$
* EM method inferences "parameter" and "responsibility" in turn with increasing precision of estimation
================================================================================
* E step
* You assume "parameters" you know are precise.
So, you "inference responsibility" which represents data is involved in which category
by using assumed parameters
$$$(\pi_k,\mu_k,\Sigma_k)$$$ --are used to inference--> $$$\pi_{ik}$$$
================================================================================
* M step
* You assume "responsibility" you know is precise
So, you inference "parameters of Gaussian mixture model" by using assumed responsibility
$$$\pi_{ik}$$$ --is used to inference--> $$$(\pi_k,\mu_k,\Sigma_k)$$$
================================================================================
* If you iterate above EM, you can make parameter and responsibility better gradually
================================================================================
* K-means clustering $$$\subset$$$ EM
If you can know "responsibility" of each data,
you can find maximal "responsibility" in which each data is involved
It means that you can perform "clustering"
$$$k_i = \arg_k\max \pi_{ik}$$$
K-means clustering is special case of EM algorithm
================================================================================
* GaussianMixture from Scikit-Learn
from sklearn.mixture import GaussianMixture
from sklearn.utils.testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
def plot_gaussianmixture(n):
# c model: GaussianMixture
model=GaussianMixture(
n_components=2,init_params='random',random_state=0,tol=1e-9,max_iter=n)
with ignore_warnings(category=ConvergenceWarning):
model.fit(X)
pi=model.predict_proba(X)
plt.scatter(X[:,0],X[:,1],s=50,linewidth=1,edgecolors="b",cmap=plt.cm.binary,c=pi[:,0])
plt.title("iteration:{}".format(n))
plt.figure(figsize=(8, 12))
plt.subplot(411)
plot_gaussianmixture(1)
plt.subplot(412)
plot_gaussianmixture(5)
plt.subplot(413)
plot_gaussianmixture(10)
plt.subplot(414)
plot_gaussianmixture(15)
plt.tight_layout()
plt.show()
 ================================================================================
General EM algorithm
* EM algorithm inferences probability distribution p(x)
when there is "random variable x"
which is dependent on latent random variable z
and when latent random variable z is not observable
but random variable x is observable
output_from_Z=random_variable_Z(result_from_trial)
ret=is output_from_Z observable
print(ret)
# False
output_from_X=random_variable_X(result_from_trial,output_from_Z)
ret=is output_from_X observable
print(ret)
# True
estimated_p(X)=EM_algorithm_to_inference_p(X)(output_from_X)
scope:network_model
ret=conditional_probability_distribution_p(X|Z,theta)
ret1=is ret determined by parameter theta?
print(ret1)
# True
ret2=you already know conditional_probability_distribution_p(X|Z,theta)?
print(ret2)
# True
scope:mixture_model
ret=is z discrete random variable?
print(ret)
# True
$$$p(x \mid \theta) = \sum_z p(x, z \mid \theta) = \sum_z q(z) p(x\mid z, \theta)$$$
Your goal in EM algorithm is to find
1. latent random variable distribution $$$q(z)$$$
2. $$$\theta$$$
which maximize likelihood $$$p(x\theta)$$$ wrt given data x
================================================================================
* First, you need to prove following equation
$$$\log p(x) \\
= \sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) -
\sum\limits_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
================================================================================
* Proof
$$$\sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)p(x \mid \theta)}{q(z)}\right) \\
=\sum\limits_z \left( q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + q(z) \log p(x \mid \theta) \right) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + \sum\limits_z q(z) \log p(x \mid \theta) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + \log p(x \mid \theta)$$$
================================================================================
* From following proven equation,
$$$\log p(x) \\
= \sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) -
\sum\limits_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
* You will write $$$L(q,\theta)$$$ and $$$KL(q|p)$$$
$$$L(q, \theta) = \sum_z q(z) \log \left(\dfrac{P(x, z \mid \theta)}{q(z)}\right)$$$
$$$KL(q \mid p) = -\sum_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
$$$\log p(x) = L(q, \theta) + KL(q \mid p)$$$
================================================================================
* $$$L(q,\theta)$$$ is "functional" which outputs "number"
when $$$L(q,\theta)$$$ is given by distribution function $$$q(z)$$$
================================================================================
* KL(q|p) is kullback leibler divergence
which shows difference between "probability distribution function $$$q(z)$$$"
and "probability distribution function $$$p(z|x,\theta)$$$"
* KL-divergence $$$\ge$$$ 0
* Therefore, L(q,\theta) is lower bound of $$$\log{p(x)}$$$
* So, L is called ELBO (evidence lower bound)
$$$\log{p(x)} \ge L(q,\theta)$$$
* Conversely, $$$\log{p(x)}$$$ is upper bound of $$$L(q,\theta)$$$
================================================================================
* If you maximize $$$L(q,\theta)$$$, $$$\log{p(x)}$$$ is maximized
* EM algorithm finds $$$q$$$ and $$$\theta$$$ values in turn and by iterative method,
to maximize $$$L(q,\theta)$$$
================================================================================
* EM algorithm
(1) E step
* You fix $$$\theta$$$ to $$$\theta_{\text{old}}$$$
* You find $$$q_{\text{new}}$$$ which maximizes $$$L(q_{\text{old}},\theta_{\text{old}})$$$
* If you can find correct $$$q_{\text{new}}$$$,
$$$L(q_{\text{new}},\theta_{\text{old}})$$$ becomes equal to upper bound $$$\log{p(x)}$$$
* That is, $$$KL(q_{\text{new}}|p)$$$ becomes 0
$$$L(q_{\text{new}},\theta_{\text{old}})=\log{p(x)}$$$
$$$KL(q_{\text{new}}|p)=0$$$
$$$q_{\text{new}}=p(z|x,\theta_{\text{old}})$$$
================================================================================
(2) M step
* You fix $$$q$$$ to current function $$$q_{\text{new}}$$$
* You find $$$\theta_{\text{new}}$$$ which maximizes $$$L(q_{\text{new}},\theta)$$$
* Since you performed maximization,
$$$L(q_{\text{new}},\theta_{\text{new}})$$$ becomes larger than previous value
$$$L(q_{\text{new}},\theta_{\text{new}}) > L(q_{\text{new}},\theta_{\text{old}})$$$
* And since $$$p(Z|X,\theta_{\text{new}})$$$ becomes different from previous value $$$p(Z|X,\theta_{\text{old}})$$$
$$$q_{\text{new}}$$$ also becomes different to $$$p(Z|X,\theta_{\text{new}})$$$
* Then, KL-divergence becomes larger than 0
* $$$q_{\text{new}} \ne p(Z|X,\theta_{\text{new}})$$$
$$$KL(q_{\text{new}}|p) > 0$$$
================================================================================
General EM algorithm
* EM algorithm inferences probability distribution p(x)
when there is "random variable x"
which is dependent on latent random variable z
and when latent random variable z is not observable
but random variable x is observable
output_from_Z=random_variable_Z(result_from_trial)
ret=is output_from_Z observable
print(ret)
# False
output_from_X=random_variable_X(result_from_trial,output_from_Z)
ret=is output_from_X observable
print(ret)
# True
estimated_p(X)=EM_algorithm_to_inference_p(X)(output_from_X)
scope:network_model
ret=conditional_probability_distribution_p(X|Z,theta)
ret1=is ret determined by parameter theta?
print(ret1)
# True
ret2=you already know conditional_probability_distribution_p(X|Z,theta)?
print(ret2)
# True
scope:mixture_model
ret=is z discrete random variable?
print(ret)
# True
$$$p(x \mid \theta) = \sum_z p(x, z \mid \theta) = \sum_z q(z) p(x\mid z, \theta)$$$
Your goal in EM algorithm is to find
1. latent random variable distribution $$$q(z)$$$
2. $$$\theta$$$
which maximize likelihood $$$p(x\theta)$$$ wrt given data x
================================================================================
* First, you need to prove following equation
$$$\log p(x) \\
= \sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) -
\sum\limits_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
================================================================================
* Proof
$$$\sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)p(x \mid \theta)}{q(z)}\right) \\
=\sum\limits_z \left( q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + q(z) \log p(x \mid \theta) \right) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + \sum\limits_z q(z) \log p(x \mid \theta) \\
=\sum\limits_z q(z) \log \left(\dfrac{p(z \mid x, \theta)}{q(z)}\right) + \log p(x \mid \theta)$$$
================================================================================
* From following proven equation,
$$$\log p(x) \\
= \sum\limits_z q(z) \log \left(\dfrac{p(x, z \mid \theta)}{q(z)}\right) -
\sum\limits_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
* You will write $$$L(q,\theta)$$$ and $$$KL(q|p)$$$
$$$L(q, \theta) = \sum_z q(z) \log \left(\dfrac{P(x, z \mid \theta)}{q(z)}\right)$$$
$$$KL(q \mid p) = -\sum_z q(z) \log \left(\dfrac{p(z\mid x, \theta)}{q(z)}\right)$$$
$$$\log p(x) = L(q, \theta) + KL(q \mid p)$$$
================================================================================
* $$$L(q,\theta)$$$ is "functional" which outputs "number"
when $$$L(q,\theta)$$$ is given by distribution function $$$q(z)$$$
================================================================================
* KL(q|p) is kullback leibler divergence
which shows difference between "probability distribution function $$$q(z)$$$"
and "probability distribution function $$$p(z|x,\theta)$$$"
* KL-divergence $$$\ge$$$ 0
* Therefore, L(q,\theta) is lower bound of $$$\log{p(x)}$$$
* So, L is called ELBO (evidence lower bound)
$$$\log{p(x)} \ge L(q,\theta)$$$
* Conversely, $$$\log{p(x)}$$$ is upper bound of $$$L(q,\theta)$$$
================================================================================
* If you maximize $$$L(q,\theta)$$$, $$$\log{p(x)}$$$ is maximized
* EM algorithm finds $$$q$$$ and $$$\theta$$$ values in turn and by iterative method,
to maximize $$$L(q,\theta)$$$
================================================================================
* EM algorithm
(1) E step
* You fix $$$\theta$$$ to $$$\theta_{\text{old}}$$$
* You find $$$q_{\text{new}}$$$ which maximizes $$$L(q_{\text{old}},\theta_{\text{old}})$$$
* If you can find correct $$$q_{\text{new}}$$$,
$$$L(q_{\text{new}},\theta_{\text{old}})$$$ becomes equal to upper bound $$$\log{p(x)}$$$
* That is, $$$KL(q_{\text{new}}|p)$$$ becomes 0
$$$L(q_{\text{new}},\theta_{\text{old}})=\log{p(x)}$$$
$$$KL(q_{\text{new}}|p)=0$$$
$$$q_{\text{new}}=p(z|x,\theta_{\text{old}})$$$
================================================================================
(2) M step
* You fix $$$q$$$ to current function $$$q_{\text{new}}$$$
* You find $$$\theta_{\text{new}}$$$ which maximizes $$$L(q_{\text{new}},\theta)$$$
* Since you performed maximization,
$$$L(q_{\text{new}},\theta_{\text{new}})$$$ becomes larger than previous value
$$$L(q_{\text{new}},\theta_{\text{new}}) > L(q_{\text{new}},\theta_{\text{old}})$$$
* And since $$$p(Z|X,\theta_{\text{new}})$$$ becomes different from previous value $$$p(Z|X,\theta_{\text{old}})$$$
$$$q_{\text{new}}$$$ also becomes different to $$$p(Z|X,\theta_{\text{new}})$$$
* Then, KL-divergence becomes larger than 0
* $$$q_{\text{new}} \ne p(Z|X,\theta_{\text{new}})$$$
$$$KL(q_{\text{new}}|p) > 0$$$





