10-01 HMM
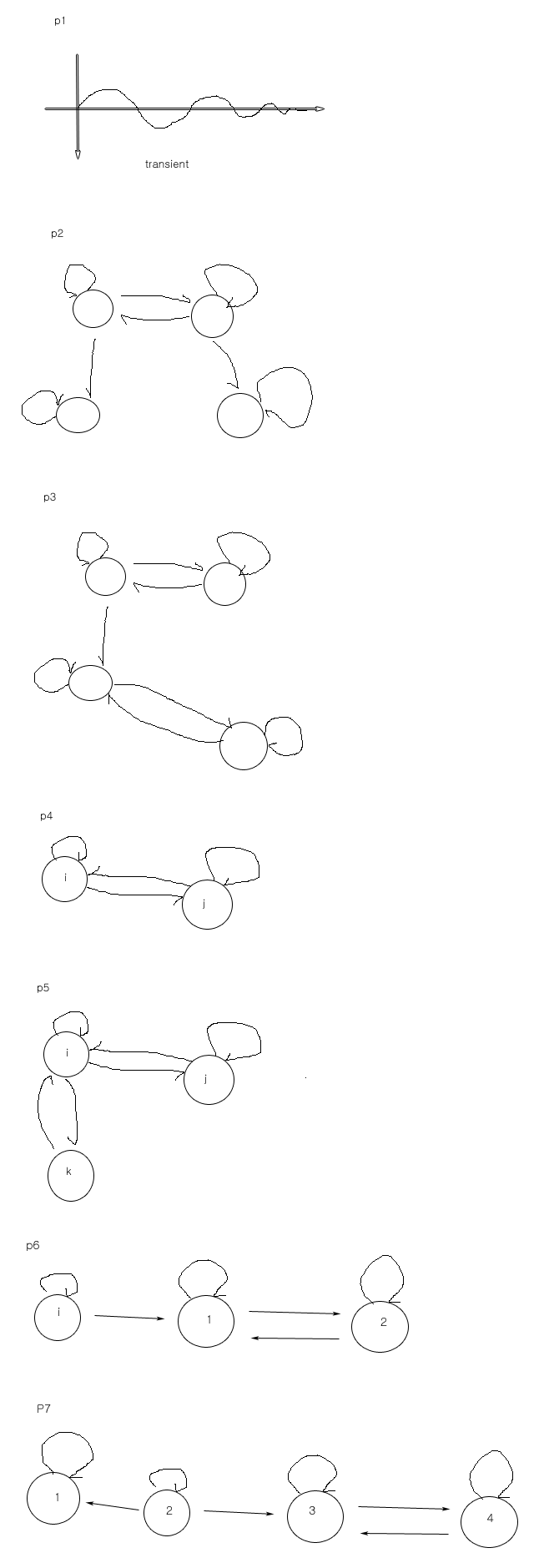
image2
@
$r_{ij}(n)$ : state i 에서 출발해서 시간 n 일때 state j 에 있을 확률이다.
markov chain 이 single recurrent class 를 가지고 있고, 그 recurrent class 가 aperiodic 한다는 두 조건 아래에서 n 이 무한대로 가면 이 확률 $r_{ij}(n)$ 이 initial state i 에 상관없이 $\pi_{j}$ 로 수렴한다.
aperiodic 관점에서 보면 시간 n 이 무한대로 가면 처음에 어디(i)에서 출발 했든지 간에 state j 에 있을 확률이 $\pi_{j}$ 의 값으로 convergence 한다.
@
p1
linear system 이나 미분방정식에서 많이 등장하는 $e_{-t}\sin{t}$ 라는 함수를 가정해보자.
t=0 일때 0이고 t 가 무한대로 가면 0으로 convergence 한다. 변화하지 않고 정상상태에 있게된다. 0으로 수렴하기 전의 모양을 transient period (잠복기) 라고 한다.
p1 e
@
p2
MC 하나를 가정하자.
두 state 는 transient state 이다. 아래 두개는 recurrent 하다. 위에서 돌다가 아래쪽 노드로 들어오면 빠져나가지 않는다. 들어가기까지 걸리는 시간에 관심을 둘 수 있다. MC 가 위쪽 노드에서 출발한다면 아랫쪽 노드들 중 하나로 들어갈텐데 각각 노드로 들어갈 확률이 어떻게 되는가 에 관심을 둘 수 있다. 아랫쪽 recurrent 한 node 에 들어가기 전의 transient 한 node 들의 behavior 를 공부하는게 transient behavior 공부의 목적이다.
p2 e
@
p3
이런 MC 을 가정하자.
돌아가다가 최종적으로 중단 node 에 들어갈것이다. 그리고 시간이 지나면서 어떻게 되는가 에 관심을 두는 것이 status behavior 이다.
p3 e
@
transient behavior 중에서 absortion probability 를 알아보자.
MC 의 recurrent class 에 들어가면 빠져나올수 없다. 이러한 recurrent class 를 통칭하여 흡수되어 빠져나올수 없다는 의미로 absorbing state 라고 한다. absortion 되기 까지 시간이 absortion time 이고 absorbing 될 확률이 absortion probability 이다.
@
Gambler's ruin : gambling 에서 최종적으로 망할확률, 성공확률을 MC 을 이용하여 분석해볼것이다.
@
state frequancy : $r_{ij}(n)$ 은 시간 n 일때 state 가 j 일 확률이라고 했다. state frequancy 는 시간 n 까지 가는 동안 state j 가 방문된 횟수 혹은 빈도를 의미한다. 전체 n 번의 transient 이 일어났다면, 혹은, n 개의 state 를 방문했다면, n 번중에서 state j 를 몇번 방문했느냐, 특정 transient 가 얼마나 자주 일어났느냐 의 의미이다.
@
state frequancy
state behavior 를 얘기 할때는 거의 아래와 같은 조건을 가정한다.
Discrete Time markov Chain 이
with a 이고
single aperiodic recurrent class 만 가진다.
@
initial state i 에서 출발해서 시간 n 이 될때 까지 state j 를 방문한 빈도 혹은 횟수는 random variable $V_{ij}(n)$ 일 것이다. 따라서, 그 횟수의 expectation 을 따져보자.
$V_{ij}(n)$ 은 시간 1에서 n 까지 가는동안 j 를 방문한 횟수를 다 더하고 Expectation 을 취해주면 된다.
Indicator function 을 사용한다. Indicator function $I_{\{A\}}$ 는 event A 가 발생하면 1이고 일어나지 않으면 0이다. 따라서, 다음과 같이 표현할수 있다.
$V_{ij}(n)=E[\sum\limits_{t=1}^{n} I_{\{X_{t}=j|X_{0}=i\}}]$
$X_{0}$ : initial state
$X_{0}$ 가 i 에서 출발했을때 시각 t 에서 state 가 j 이면 1 그렇지 않으면 0 이라는 뜻이다.
따라서 시간 t =1 에서 t=n 까지 다 더하면 state j 를 방문한 총 횟수가 계산된다.
event A 가 있다면 $I_{\{A\}}$ 가 random variable 이다.
$E[I_{\{A\}}]$ 은 $1\times$(1이 발생할 확률, 즉, A가 발생할 확률)+$0\times$(A가 일어나지 않을 확률) 이므로 A가 발생활 확률 P(A) 이다.
sum 의 expectation 은 expectation 의 sum 인 성질을 이용해 다음과 같이 정리한다.
$V_{ij}(n)=E[\sum\limits_{t=1}^{n} I_{\{X_{t}=j|X_{0}=i\}}]$
$V_{ij}(n)=\sum\limits_{t=1}^{n} E[I_{\{X_{t}=j|X_{0}=i\}}]$
$E[I_{\{A\}}]$ 은 event A의 확률 P(A) 임을 이용한다.
event ${\{X_{t}=j|X_{0}=i\}}$ 의 확률은 i에서 출발해서 시각 t 에서 j 일 확률인 $r_{ij}(t)$ 이다. 따라서\
$V_{ij}(n)=\sum\limits_{t=1}^{n} r_{ij}(t)$
빈도로 나타내 보자. initial state $X_{0}=i$ 에서 출발해서 시간 1부터 n까지 총 n 개의 state 를 방문할것이다. 그 중에서 state j 를 방문한게 몇번이냐를 표현하는 $\frac{1}{n}V_{ij}(n)$ 를 구해보자.
그리고 위의 수식에서 시간 n 이 무한대로 갈때 $\lim_{n\to\infty} \frac{1}{n}V_{ij}(n)$ 를 생각해보자.
위에 구한 수식의 관계로 부터 다음과 같이 쓸수 있다.
$\lim\limits_{n\to\infty} \frac{1}{n}V_{ij}(n) = \lim\limits_{n\to\infty} \frac{1}{n} \sum\limits_{t=1}^{n} r_{ij}(t)$
처음에 했던 가정으로 부터 $r_{ij}(t)$ 은 t 가 무한대로 가면 $\pi_{j}$ 로 convergence 한다. 따라서,
$\lim\limits_{n\to\infty} \frac{1}{n}V_{ij}(n) = \lim\limits_{n\to\infty} \frac{1}{n} \sum\limits_{t=1}^{n} r_{ij}(t)=\pi_{j}$ 이다.
@
$\pi_{j}$ 는 시간 n 이 무한대로 갈때(MC 이 많이 진행됐을때) state j 에 있을 확률이었다.
$\lim\limits_{n\to\infty} \frac{1}{n}V_{ij}(n) = \lim\limits_{n\to\infty} \frac{1}{n} \sum\limits_{t=1}^{n} r_{ij}(t)=\pi_{j}$ 를 보면 $\pi_{j}$ 를 다른식으로도 해석할 수 있는데, 시간 n 이 무한대로 갈때(MC 이 많이 진행됐을때) state j 가 방문된 빈도라고 볼수 있다는 것이다.
@
p4
이제 transient frequancy 를 알아 보자. i, j node 로 구성되어 있는 MC 을 그려보자.
출발하고 돌아다니면서 MC 가 진행된다. 그 때 j 를 방문한 빈도를 위에서 고찰해봤다면, transient frequancy 는 transient 이 일어난 frequancy 를 따지는게 transient frequancy 이다.
p4 e
@
transient frequancy 는 위에서 봤던 똑같은 condition
1. Discrete Time Markov Chain is with a
2. Discrete Time Markov Chain has a single aperiodic recurrent class
과 더불어서
MC 가 시간 n 까지 진행됐을때, state j 에서 state k 로 transient 이 일어난 횟수(random variable, $q_{jk}(n)$ ) 의 expectation 이다.
@
결과를 놓고 고찰해 보자. j 에서 k 로 transient 이 일어나려면 일단 state 가 j 에 있어야 한다. 이 때, 시간 n 이 무한대로 간다면 state j 에 있을 확률은 $\pi_{j}$ 이다. j 에서 k 로 transient 이 일어날 확률은 $\pi_{j} P_{jk}$ 가 된다.
@
p5
initial state 가 randomly 하게 출발 했을때, 시간 1 까지 흘렀을때 j에서 k로 transient 이 한번 발생하려면 시간 0일때 state 가 j 에 있어야 하고 시간 1일때 state 가 k 에 있어야 한다.
즉, $X_{0}=j \cap X_{1}=k$ 이면 j 에서 k 로 transient 가 일어나는 것이다.
p5 e
@
위의 내용을 아래에 적용해본다.
$q_{jk}(n)$ 은 바로 이전 시각이 j 였다가 $X_{t-1}=j$ 그 다음 시점에서의 state 가 k 가 되는 $X_{t}=k$ 인 Indicator function 을 t=1 에서 t=n 까지 진행하면서 더한것의 expectation 이 $q_{jk}(n)$ 의 정의이다.
$q_{jk}(n)=E[\sum\limits_{t=1}^{n} I_{\{X_{t}=k, X_{t-1}=j\}}]$
@
initial state 는 일단 고려하지 않는다. 그러면 다음과 같이 수식을 정리 할수 있다.
$q_{jk}(n)=E[\sum\limits_{t=1}^{n} I_{\{X_{t}=k, X_{t-1}=j\}}]$
$q_{jk}(n)=\sum\limits_{t=1}^{n} E[I_{\{X_{t}=k, X_{t-1}=j\}}]$
$q_{jk}(n)=\sum\limits_{t=1}^{n} P(X_{t}=k, X_{t-1}=j)$
$q_{jk}(n)=\sum\limits_{t=1}^{n} P(X_{t}=k \cap X_{t-1}=j)$
우리는 j 에서 k 로 transient 이 일어날 확률 $P_{jk}$ 를 알고 있다. 이때, $\pi_{j}P_{jk}$ 를 도출하고 싶다.
conditional probability 의 Definition 을 이용해 다음과 같이 변형한다.
$q_{jk}(n)=\sum\limits_{t=1}^{n} P(X_{t-1}=j) P(X_{t}=k|X_{t-1}=j)$
우리는 $P(X_{t}=k|X_{t-1}=j)=P_{kj}$ 임을 알고있다. 따라서,
$q_{jk}(n)=\sum\limits_{t=1}^{n} P(X_{t-1}=j) P_{jk}$
initial state 를 모를때도 수식을 진행할 수 있다.
initial state 를 모르는 상태에서 시각이 t-1 일때, state 가 j 에 있을 확률 $P(X_{t-1}=j)$ 이 어떻게 되는가?
$P(X_{t-1}=j)$ 에 total probability theorem 을 써서 정리하면서 알아낼 수 있다.
더 간편한 방법은 $X_{0}=i$ 처럼 initial state 를 i 라고 가정으르 하고 진행하는게 더 간편하다.
그런데 여기서에서는 total probability theorem 을 써본다
그리고 위 수식에 total probability theorem 을 적용해서 정리해보자.
$q_{jk}(n)= \sum\limits_{t=1}^{n} \sum\limits_{i=1}^{m} P(X_{0}=i) P(X_{t-1}=j|X_{0}=i) P_{jk}$
$q_{jk}(n)= \sum\limits_{t=1}^{n} \sum\limits_{i=1}^{m} P(X_{0}=i) r_{ij}(t-1) P_{jk}$
빈도를 따져보기 위해서 lim 를 취한다.
$\lim\limits_{n\to\infty} \frac{1}{n} q_{jk}(n) = \lim\limits_{n\to\infty} \frac{1}{n} \sum\limits_{t=1}^{n} \sum\limits_{i=1}^{m} P(X_{0}=i) r_{ij}(t-1) P_{jk}$
t 가 무한대로 가면 $\sum\limits_{i=1}^{m} P(X_{0}=i) r_{ij}(t-1) P_{jk}$ 에서 t 에 의해 변하는 부분은 $r_{ij}(t-1)$ 부분밖에 없고 $\pi_{j}$ 로 convergence 한다. $\sum\limits_{i=1}^{m} P(X_{0}=i)=1$ 이므로 $\sum\limits_{i=1}^{m} P(X_{0}=i) r_{ij}(t-1) P_{jk}$ 은 $\pi_{j}P_{jk}$ 로 convergence 한다.
@
우리의 intuition 에 맞는 것은 j 에서 k 로 transient 가 일어나려면 반복해 얘기하지만 먼저 state j 에서 있었어야하고 그 뒤 j 에서 k 로 transient 가 일어날 수 있다. 그래서 $\pi_{J}P_{jk}$ 이렇게 쓸 수 있는 것이다.
@
지난 시간에 $\pi_{j} = \sum\limits_{k=1}^{m} \pi_{k} P_{kj}$ 로 썼다.
m 은 모든 state 의 갯수를 의미한다.
첫번째 시간에 markov chain 을 정의할 때, markov chain 이 취할 수 있는 state S 가 S={1, ..., m} 이 된다고 하였다.
$\pi_{k} P_{kj}$ 를 위의 수식의 해석으로 본다면 k 에서 j 로 transient 이 일어난 빈도로 확률을 해석 할 수 있었다. 모든 k 에 대해서 다 더하면 j 에 있을 확률 $\pi_{j}$ 이 된다.
@
$V_{jk}(n)$ 의 해석 : initial state j 에서 출발하여 시간 n 이 될 때까지 k 를 방문한 횟수
$q_{jk}(n)$ 의 해석 : j 에서 k 로 transient 이 발생한 횟수
@
$V_{jk}(n)$ 에서 n 이 무한대로 가면 $\pi_{j}$ 로 convergence 한다. 라는 것은 약속이라기 보다 위에서 언급된 condition 이 성립하면 성립하는 명제이다.
@
p6
위의 내용은 markov chain example 을 하나 생각해 보면 된다.
i, 1, 2 라고 가정해보자. i에서 출발을 했다. 그러다가 본인으로 돌다가 1로 들어가면 i 로는 더 이상 방문이 안된다. 시간 n 이 무한대로 갔을때, 출발을 i 에서 하든 1에서 하든, 어떤 state 에 있을 확률은 출발점과 무관 할 것이다. i 에서 출발해서 돌다가 1로 들어가면 그 이전의 일들은 다 잊혀지는것, 혹은 마치 1이 새로운 출발점이 되는 것과 같다.
p6 e
@
p7
그런데 recurrent class 가 두개라면 얘기가 달라진다. 1 에서 출발하면 2, 3, 4 전부 0이 되어 의미가 없어진다. 1에서 출발하면 1,2 가 의미가 없어진다. 그래서 recurrent class 는 하나라고 가정을 해야 initial state 에 상관없이..
p7 e
@
Birth-death process 에 대해 알아보자.
state node 들이 다양하게 있고 state transient 도 다양하게 일어날 수 있는 것이 markov chain 인데 birth-death process 는 state 들이 linear 하고 transient 는 서로 이웃한 것들끼리만 일어날 수 있는 markov chain 이다.
@
Birth-death process 는 network 에서 queuing delay, 어떤 service system 에 들어갔을 때 얼만큼 기다려야 하냐 혹은 service 를 받고 나가는데 얼마나 시간이 걸리느냐 같은 것들, 를 분석할때 자주 사용되는 markov chain 이다.
@
p8
transient 는 자기 자신과 이웃한 state node 끼리만 일어난다.
사람이 태어나고 죽는 사례가 대표적 예시가 된다.
태어나서 인구가 1명이 된다. 또한명이 태어나면 2명이 된다. 한명이 죽으면 1명이 된다.
0명이었을 때 한명이 태어날 확률을 $b_{0}$, 1명이었을때 죽을 확률 $d_{1}$, 0에서 0으로 recurrent 는 아무일도 일어나지 않을 확률 $1-b_{0}-0$, 1명이었을때 1명이 더 태어날 확률 $b_{1}$, 2명이었을 때 1명이 죽을 확률 $d_{2}$, 1에서 1로 recurrent 할 확률 $1-b_{1}-d_{1}$, $1-b_{2}-d_{2}$, $b_{3}$, $d_{3}$, ..., $b_{n-1}$, $d_{n}$, recurrent on (n-1) : $1-b_{n-1}-d_{n-1}$, recurrent on m : $1-d_{n}$
markov chain 의 state 가 인구를 나타낸다면, 시간 n 이 무한대로 갔을때, 인구가 2명일 확률은? 3명인 확률은? n 명일 확률은? 이런걸 따져볼 수 있다.
@
계산 편의를 위해 birth, death 확률이 모든 state 에서 같다고 가정한다.
위에서 j 에서 k 로 transient 이 일어나는 빈도는 시간 n 이 무한대로 갈때 $\pi_{j} P_{jk}$ 로 convergence 된다고 위에서 얘기했다.
state 1 에서 2 가는 빈도는 $\pi_{1} b$, state 2 에서 1로 가는 빈도는 $\pi_{2} d$ 이다.
두 값은 똑같아야 한다.
$\pi_{1}b=\pi_{2}d$
p8
@
$\pi=\pi P$
$\pi_{1} = \sum\limits_{k=0}^{m} \pi_{k} P_{kj}$
state transient 가 이웃한 state node 들끼리만 일어난다.
state 1 에서는 0 또는 2 에서 올수밖에 없다. 따라서,
$\pi_{1} = \pi_{0} P_{01} + \pi_{2} P_{21}$
$P_{01} = b, P_{21} = d$ 이므로
$\pi_{1} = \pi_{0} b + \pi_{2} d$
따라서, 정리하면 위의 $\pi_{1}b=\pi_{2}d$ 식을 유도할 수 있다.
이웃한 transient 끼리 balance 가 일어나야 한다고 해서 $\pi_{1}b=\pi_{2}d$ 를 balance equation 이라고 하기도 한다. 이 balance equation 이 모든 transient 사이에서 성립함을 알 수 있다.
@
balance equation 을 일반적으로 쓰면 $\pi_{i} b = \pi_{i+1} d$, i=0, ..., n-1
$\pi_{i+1} = \frac{b}{d} \pi_{i}$ 이고 $\frac{b}{d}=\rho$ 라고 정의해보자. 그러면,
$\pi_{i} = \rho^{i} \pi_{0}$ i=0,...n 으로 쓸 수 있다.
이때, $\pi_{0}$ 값만 알면 다 알게 된다.
$\pi_{0}$ 은 아래와 같이 구한다.
...therem에 의해서 또는 직관적으로도 시간 n 이 무한대로 갈때, 0,1,...,n 에 있을 각각의 확률이므로 합이 1이여야하므로
$\pi_{0} + \pi_{1} + ... + \pi_{n} = 1$
위 구한 식에 의해서
$\pi_{0}=\rho^{0} \pi_{0}$
$\pi_{1}=\rho^{1} \pi_{0}$
...
$\pi_{n}=\rho^{n} \pi_{0}$
대입하면
$\pi_{0}(1+\rho^{1}+...+\rho^{n})=1$
따라서,
$\pi_{0}= \frac{1-\rho}{1-\rho^{n+1}}$ when $\rho\neq 1$
$\pi_{0}= \frac{1}{n+1}$ when $\rho= 1$
또한,
$\pi_{i}= \rho^{i} \frac{1-\rho}{1-\rho^{n+1}}$ when $\rho\neq 1$
$\pi_{i}= \frac{1}{n+1}$ when $\rho= 1$ 이기도 하다.
@
$\rho=1$ 은 태어날 확률 b와 죽을 확률 d 가 같은 상황이다. 그럴때는 각각의 state 에서의 확률 $\pi_{i} = \frac{1}{n+1}$ 이다.
@
transient behavior 에 대해 알아보자.
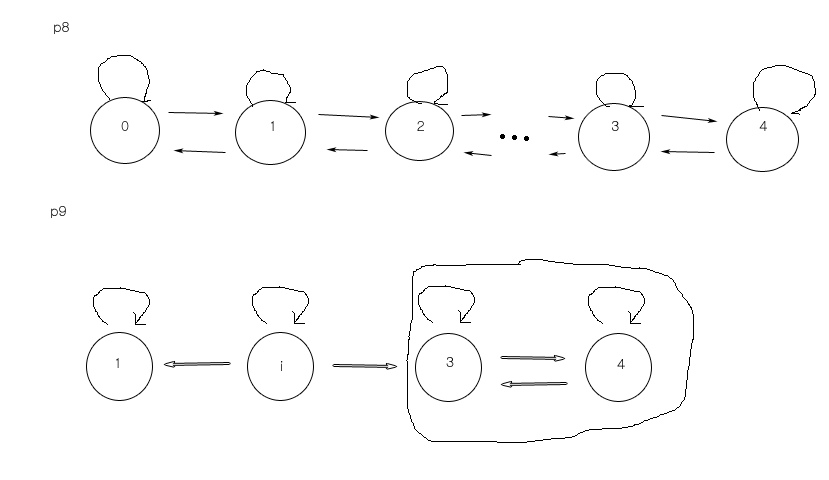
p9
markov chain 을 그려보자.
absorbing state 란 한번 들어가면 나올수 없는 1 같은 state node 이다. absortion probability 에서 관심있는 건 이러한 absorbing state 에 들어갈 확률이 얼마인가 에 관한 것이다. i에서 출발했다면 이 확률이 1은 아니다. 1에서 출발했다면 확률이 1이다. 2 에서 출발해도 확률은 0이다. initial state 에 따라서 absortion probability 가 달라진다. 3,4같이 recurrent class 로 들어가면 못 빠져 나온다. recurrent class 를 하나의 state로 바꿔서 계산해도 absortion probability 를 구할 수 있다.
@
absortion probability
1. 1 또는 3+4 중 하나 처럼 absorbing state S 하나로 고정을 시킨다.
absorbing state 를 확률수식으로 표현하면 $P_{ss}=1, P_{sj}=0 \forall j\neq s$
자기한테만 trasition 만 일어나는.
2. $a_{i}$ 은 markov chain 에서 i에서 출발해서 시간 n 에서의 state $X_{n}$ 가 궁극적으로 state s 가 되는 확률 $P(X_{n} eventually becomes S|X_{i})$ 로 정의 될 수 있다.
$a_{i} = P(X_{n} eventually becomes S|X_{i})$

