* Bayes_theorem
================================================================================
Bayes theorem is equation which is simplified version from conditional probability
to use Bayes theorem for pattern recognition
================================================================================
* $$$B_1, B_2, \cdots, B_N$$$: events which consists of sample space S
* $$$B_1, B_2, \cdots, B_N$$$: independent to each other
* Event A is composed of multiple events of B
* Question: when event A occured, probability of A occurring in event $$$B_j$$$
================================================================================
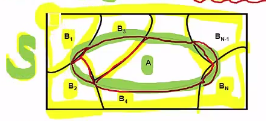 * S: sample space
* S is composed of multiple events Bs
* A: set of event
* when A occured, A occurred from $$$B_1$$$ or $$$B_2$$$ or?
================================================================================
* Bayes theorem is expression of above situation
* $$$P[B_j|A] \;\;\;\; (1) \\
= \dfrac{P[A\cap B_j]}{P[A]} \;\;\;\; (2) \\
= \dfrac{P[A|B_j]P[B_j]}{\sum\limits_{k=1}^N P[A|B_k]P[B_k]} \;\;\;\; (3)$$$
* $$$P[B_j|A]$$$: conditional probability
when event A occured, the probability value of "$$$A$$$ occured from $$$B_j$$$"
* (1) -> (2): conditional probability
================================================================================
* S: sample space
* S is composed of multiple events Bs
* A: set of event
* when A occured, A occurred from $$$B_1$$$ or $$$B_2$$$ or?
================================================================================
* Bayes theorem is expression of above situation
* $$$P[B_j|A] \;\;\;\; (1) \\
= \dfrac{P[A\cap B_j]}{P[A]} \;\;\;\; (2) \\
= \dfrac{P[A|B_j]P[B_j]}{\sum\limits_{k=1}^N P[A|B_k]P[B_k]} \;\;\;\; (3)$$$
* $$$P[B_j|A]$$$: conditional probability
when event A occured, the probability value of "$$$A$$$ occured from $$$B_j$$$"
* (1) -> (2): conditional probability
================================================================================
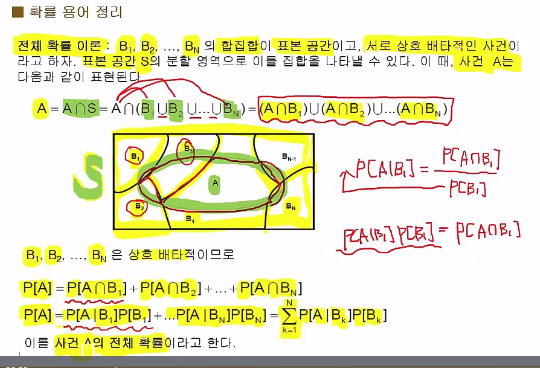 * Law of total probability of event A:
$$$P[A] \\
= P[A|B_1]P[B_1] + \cdots + P[A|B_N]P[B_N] \\
= \sum\limits_{k=1}^N P[A|B_k]P[B_k]$$$
================================================================================
In (3), you replace $$$P[A]$$$ with $$$\sum\limits_{k=1}^N P[A|B_k]P[B_k]$$$
================================================================================
In (3), according to following conditional probability theorem,
$$$P[A\cap B_j] \\
= P[A|B_j]P[B_j] \\
= P[B_j|A]P[A]$$$
you can replace $$$P[A\cap B_j] with P[A|B_j]p[B_j]$$$
================================================================================
* Let's see Bayes theorem in terms of pattern recognition.
* $$$P[\omega_j|x] \;\;\;\; (1) \\
= \dfrac{P[x|\omega_j]P[\omega_j]}{\sum\limits_{k=1}^N P[x|\omega_k]P[\omega_k]} \;\;\;\; (2) \\
= \dfrac{P[x|\omega_j]P[\omega_j]}{P[x]} \;\;\;\; (3) $$$
* $$$w_j$$$: jth class, like $$$\omega_1=\text{male}$$$, $$$\omega_2=\text{female}$$$
* $$$x$$$: feature vector, like weight data $$$x_1=[70,60]$$$, $$$x_2=[40,50]$$$
* $$$P[\omega_j]$$$: prior probability of "class $$$\omega_j$$$" occuring
* $$$P[\omega_j|x]$$$: posterior probability of $$$\omega_j$$$ wrt feature vector x
when feature vector x occurred, probability of feature vector x occurring from class $$$\omega_j$$$
* $$$P[x|\omega_j]$$$: likelihood,
when class \omega_j occurred, probability of x occurring from $$$\omega_j$$$
================================================================================
* Goal you would ultimately like to solve: $$$P[\omega_j|x]$$$
when feature vector x is given, which class $$$\omega_j$$$ has that feature vector x?
* You will get probability values on each class
$$$\omega_{\text{male}}=0.7$$$
$$$\omega_{\text{female}}=0.3$$$
* You can decide class is $$$\omega_{\text{male}}$$$
================================================================================
* Law of total probability of event A:
$$$P[A] \\
= P[A|B_1]P[B_1] + \cdots + P[A|B_N]P[B_N] \\
= \sum\limits_{k=1}^N P[A|B_k]P[B_k]$$$
================================================================================
In (3), you replace $$$P[A]$$$ with $$$\sum\limits_{k=1}^N P[A|B_k]P[B_k]$$$
================================================================================
In (3), according to following conditional probability theorem,
$$$P[A\cap B_j] \\
= P[A|B_j]P[B_j] \\
= P[B_j|A]P[A]$$$
you can replace $$$P[A\cap B_j] with P[A|B_j]p[B_j]$$$
================================================================================
* Let's see Bayes theorem in terms of pattern recognition.
* $$$P[\omega_j|x] \;\;\;\; (1) \\
= \dfrac{P[x|\omega_j]P[\omega_j]}{\sum\limits_{k=1}^N P[x|\omega_k]P[\omega_k]} \;\;\;\; (2) \\
= \dfrac{P[x|\omega_j]P[\omega_j]}{P[x]} \;\;\;\; (3) $$$
* $$$w_j$$$: jth class, like $$$\omega_1=\text{male}$$$, $$$\omega_2=\text{female}$$$
* $$$x$$$: feature vector, like weight data $$$x_1=[70,60]$$$, $$$x_2=[40,50]$$$
* $$$P[\omega_j]$$$: prior probability of "class $$$\omega_j$$$" occuring
* $$$P[\omega_j|x]$$$: posterior probability of $$$\omega_j$$$ wrt feature vector x
when feature vector x occurred, probability of feature vector x occurring from class $$$\omega_j$$$
* $$$P[x|\omega_j]$$$: likelihood,
when class \omega_j occurred, probability of x occurring from $$$\omega_j$$$
================================================================================
* Goal you would ultimately like to solve: $$$P[\omega_j|x]$$$
when feature vector x is given, which class $$$\omega_j$$$ has that feature vector x?
* You will get probability values on each class
$$$\omega_{\text{male}}=0.7$$$
$$$\omega_{\text{female}}=0.3$$$
* You can decide class is $$$\omega_{\text{male}}$$$
================================================================================
 * To know $$$P[\omega_j|x]$$$ by using Bayes theorem, you should know followings:
1. $$$P[x]$$$: probability value of feature vector x occurs
2. $$$P[\omega_j]$$$: probability value of each class occuring
3. $$$P[x|\omega_j]$$$: probability value of feature vector x occuring
from given class $$$\omega_j$$$
================================================================================
1. $$$P[\omega_j]$$$: prior probability of $$$\omega_j$$$
probability value of class $$$\omega_j$$$ occuring
2. $$$P[\omega_j|x]$$$: posterior probability of $$$\omega_j$$$ wrt feature vector x
after you've got feature vector x,
probability value of "x came from class $$$\omega_j$$$"
3. $$$P[x|\omega_j]$$$: likelihood,
probability value of x occuring when $$$\omega_j$$$ is given
For example, probability of height feature vector [170,180] occuring from class male
and probability of height feature vector [160,162] occuring from class female are different.
Probability values of feature vector occuring are different per class.
4. P[x]: probability value of given pattern x occuring,
non-influencial to the classification,
which is used as normalization constant term.
================================================================================
* Pattern recognition using Bayes theorem
* With constant term
$$$\text{posterior probability}=\dfrac{\text{likelihood}\times \text{prior probability}}{\text{normalization term}}$$$
* Without constant term
$$$\text{posterior probability}=\text{likelihood} \times \text{prior probability}$$$
================================================================================
Example
* law of the total probability
================================================================================
Example
* Bayes theorem
================================================================================
* To know $$$P[\omega_j|x]$$$ by using Bayes theorem, you should know followings:
1. $$$P[x]$$$: probability value of feature vector x occurs
2. $$$P[\omega_j]$$$: probability value of each class occuring
3. $$$P[x|\omega_j]$$$: probability value of feature vector x occuring
from given class $$$\omega_j$$$
================================================================================
1. $$$P[\omega_j]$$$: prior probability of $$$\omega_j$$$
probability value of class $$$\omega_j$$$ occuring
2. $$$P[\omega_j|x]$$$: posterior probability of $$$\omega_j$$$ wrt feature vector x
after you've got feature vector x,
probability value of "x came from class $$$\omega_j$$$"
3. $$$P[x|\omega_j]$$$: likelihood,
probability value of x occuring when $$$\omega_j$$$ is given
For example, probability of height feature vector [170,180] occuring from class male
and probability of height feature vector [160,162] occuring from class female are different.
Probability values of feature vector occuring are different per class.
4. P[x]: probability value of given pattern x occuring,
non-influencial to the classification,
which is used as normalization constant term.
================================================================================
* Pattern recognition using Bayes theorem
* With constant term
$$$\text{posterior probability}=\dfrac{\text{likelihood}\times \text{prior probability}}{\text{normalization term}}$$$
* Without constant term
$$$\text{posterior probability}=\text{likelihood} \times \text{prior probability}$$$
================================================================================
Example
* law of the total probability
================================================================================
Example
* Bayes theorem
================================================================================


