/mnt/1T-5e7/mycodehtml/ML_theory/PRJJ/006_Random_variable_Probability_distribution/001.html
================================================================================
What is the probability?
Let's see probabilty as distribution state
So, you should know what is the probability distribution
Before that, you should know what is the random variable
================================================================================
* $$$P(X=3)=\dfrac{1}{6}$$$
* Probability of 3 occurring when you roll the dice
* Probability of random variable X having 3 when you roll the dice
================================================================================
* Radom variable is function
1=random_variable_function(trial_result_by_rolling_a_dice)
2=random_variable_function(trial_result_by_rolling_a_dice)
# ...
6=random_variable_function(trial_result_by_rolling_a_dice)
================================================================================
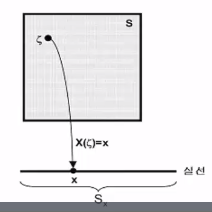 $$$S$$$: sample space
$$$\zeta$$$: result from trial
$$$X()$$$: random variable
$$$x$$$: real number
================================================================================
discrete_numbers_like_integers=discrete_random_variable(result_from_trials)
continuous_numbers_like_real_numbers=continuous_random_variable(result_from_trials)
================================================================================
Results from trial which can be assigned into random variable will have some distribution.
For example, some result occurs more often (that result has high probability value),
some occurs more less (that result has low probability value).
Probability values which are assigned to each result can have some distribution or pattern.
That pattern is called probability distribution.
================================================================================
probability_value=probability_distribution_function(result_from_trial)
================================================================================
$$$S$$$: sample space
$$$\zeta$$$: result from trial
$$$X()$$$: random variable
$$$x$$$: real number
================================================================================
discrete_numbers_like_integers=discrete_random_variable(result_from_trials)
continuous_numbers_like_real_numbers=continuous_random_variable(result_from_trials)
================================================================================
Results from trial which can be assigned into random variable will have some distribution.
For example, some result occurs more often (that result has high probability value),
some occurs more less (that result has low probability value).
Probability values which are assigned to each result can have some distribution or pattern.
That pattern is called probability distribution.
================================================================================
probability_value=probability_distribution_function(result_from_trial)
================================================================================
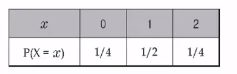 0=random_variable_X(trial_result_from_rolling_a_dice)
1=random_variable_X(trial_result_from_rolling_a_dice)
2=random_variable_X(trial_result_from_rolling_a_dice)
================================================================================
1/4=probability_distribution_function(0)
1/2=probability_distribution_function(1)
1/4=probability_distribution_function(2)
1/4,1/2,1/4: probability distribution
================================================================================
Probability distribution functions: CDF, PDF, PMF
================================================================================
Cumulitive (probability) distribution function:
* $$$F_X(x) = P[X\le x]$$$
* for $$$-\infty < x < \infty$$$
* $$$X$$$: random variable
================================================================================
If x=80kg, possible $$$X=10,20,\cdots,79.999$$$
================================================================================
0=random_variable_X(trial_result_from_rolling_a_dice)
1=random_variable_X(trial_result_from_rolling_a_dice)
2=random_variable_X(trial_result_from_rolling_a_dice)
================================================================================
1/4=probability_distribution_function(0)
1/2=probability_distribution_function(1)
1/4=probability_distribution_function(2)
1/4,1/2,1/4: probability distribution
================================================================================
Probability distribution functions: CDF, PDF, PMF
================================================================================
Cumulitive (probability) distribution function:
* $$$F_X(x) = P[X\le x]$$$
* for $$$-\infty < x < \infty$$$
* $$$X$$$: random variable
================================================================================
If x=80kg, possible $$$X=10,20,\cdots,79.999$$$
================================================================================
 CDF deals with probability values of X is less than 100, 200, etc
================================================================================
Characteristics of cumulitive distribution function
* $$$0\le F_X(x) \le 1$$$
* $$$\lim\limits_{x\to\infty} F_X(x)=1$$$
* $$$\lim\limits_{x\to-\infty} F_X(x)=0$$$
* $$$F_X(a) \le F_X(b)$$$, if $$$a\le b$$$
================================================================================
CDF deals with probability values of X is less than 100, 200, etc
================================================================================
Characteristics of cumulitive distribution function
* $$$0\le F_X(x) \le 1$$$
* $$$\lim\limits_{x\to\infty} F_X(x)=1$$$
* $$$\lim\limits_{x\to-\infty} F_X(x)=0$$$
* $$$F_X(a) \le F_X(b)$$$, if $$$a\le b$$$
================================================================================
 1. continuous_values=continuous_random_variable(trial_result)
2. discrete_values=discrete_random_variable(trial_result)
================================================================================
prob_value=probability_density_function(continuous_value_from_RV)
prob_value=probability_mass_function(discrete_value_from_RV)
================================================================================
PDF
* $$$f_X(x)$$$
* X: continuous randome variable
* $$$f_X(x)=\frac{d}{dX} F_X(x)$$$
================================================================================
PDF $$$\simeq$$$ PMF
$$$f_X(x)=\frac{\Delta F_X(x)}{\Delta X}$$$
because discrete variable can be differentiated, you use $$$\Delta$$$ than d
================================================================================
* $$$f_X(x)>0$$$
* $$$P[a\lt x \lt b] = \int_a^b f_X(x)dx$$$
* $$$F_X(x)=\int_{-\infty}^{\infty} f_X(x)dx$$$
* $$$1=\int_{-\infty}^{\infty} f_X(x) dx$$$
* $$$f_X(x|A)=\dfrac{d}{dx}F_X(x|A)$$$ where $$$F_X(x|A)=\dfrac{P[\{X\lt x\}\cap A]}{P[A]}$$$ if $$$P[A]>0$$$
================================================================================
Meaning of probability density function
1. continuous_values=continuous_random_variable(trial_result)
2. discrete_values=discrete_random_variable(trial_result)
================================================================================
prob_value=probability_density_function(continuous_value_from_RV)
prob_value=probability_mass_function(discrete_value_from_RV)
================================================================================
PDF
* $$$f_X(x)$$$
* X: continuous randome variable
* $$$f_X(x)=\frac{d}{dX} F_X(x)$$$
================================================================================
PDF $$$\simeq$$$ PMF
$$$f_X(x)=\frac{\Delta F_X(x)}{\Delta X}$$$
because discrete variable can be differentiated, you use $$$\Delta$$$ than d
================================================================================
* $$$f_X(x)>0$$$
* $$$P[a\lt x \lt b] = \int_a^b f_X(x)dx$$$
* $$$F_X(x)=\int_{-\infty}^{\infty} f_X(x)dx$$$
* $$$1=\int_{-\infty}^{\infty} f_X(x) dx$$$
* $$$f_X(x|A)=\dfrac{d}{dx}F_X(x|A)$$$ where $$$F_X(x|A)=\dfrac{P[\{X\lt x\}\cap A]}{P[A]}$$$ if $$$P[A]>0$$$
================================================================================
Meaning of probability density function
 What you deal with is probability value itself than probability density
But mathematically, it's fair to say
that only probability density exists in probability density function
because you deal with "continuous" random variable X
You cap perform integration in interval on that probability density,
then, result of integration becomes probability
================================================================================
In case of probability mass function, function becomes probability itself.
================================================================================
What you deal with is probability value itself than probability density
But mathematically, it's fair to say
that only probability density exists in probability density function
because you deal with "continuous" random variable X
You cap perform integration in interval on that probability density,
then, result of integration becomes probability
================================================================================
In case of probability mass function, function becomes probability itself.
================================================================================




