================================================================================
Joint CDF, Joint PDF: when there are over-2 random variances
================================================================================
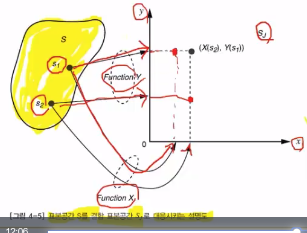 * $$$S$$$: sample sapce where population resides in
* $$$S_J$$$: joint sample space
* $$$s_1, s_2$$$: 2 samples
* 2 random variables: X and Y
================================================================================
s_1_x_in_S_J=random_variable_X(s_1)
s_1_y_in_S_J=random_variable_Y(s_1)
s_2_x_in_S_J=random_variable_X(s_2)
s_2_y_in_S_J=random_variable_Y(s_2)
================================================================================
* $$$S$$$: sample sapce where population resides in
* $$$S_J$$$: joint sample space
* $$$s_1, s_2$$$: 2 samples
* 2 random variables: X and Y
================================================================================
s_1_x_in_S_J=random_variable_X(s_1)
s_1_y_in_S_J=random_variable_Y(s_1)
s_2_x_in_S_J=random_variable_X(s_2)
s_2_y_in_S_J=random_variable_Y(s_2)
================================================================================
 Area in joint sample space
================================================================================
Vector random variable
* Univariate random variable
(1) CDF
1) $$$P_X(x) = P \{ X \le x \}$$$
2) $$$P_Y(y) = P \{ Y \le y \}$$$
* Bivariate vector random variable
(1) CDF
1) $$$F_{X,Y}(x,y) = P \{ X\le x, Y\le y \}$$$
2) $$$P \{ X\le x, Y\le y \} = P(A\cap B)$$$
================================================================================
When random vector X=[x_1,x_2,\cdots,x_N]^T is given,
(1) Joint CDF: $$$F_X(x) = P_X [ \{ X_1 \le x_1 \} \cap \{ X_2 \le x_2 \} \cap \cdots \cap \{ X_N \le x_N \} ]$$$
(2) Joint PDF: $$$f_X(x) = \dfrac{\partial^N F_X(x)}{ \partial x_1 \partial x_2 \cdots \partial x_N }$$$
================================================================================
Area in joint sample space
================================================================================
Vector random variable
* Univariate random variable
(1) CDF
1) $$$P_X(x) = P \{ X \le x \}$$$
2) $$$P_Y(y) = P \{ Y \le y \}$$$
* Bivariate vector random variable
(1) CDF
1) $$$F_{X,Y}(x,y) = P \{ X\le x, Y\le y \}$$$
2) $$$P \{ X\le x, Y\le y \} = P(A\cap B)$$$
================================================================================
When random vector X=[x_1,x_2,\cdots,x_N]^T is given,
(1) Joint CDF: $$$F_X(x) = P_X [ \{ X_1 \le x_1 \} \cap \{ X_2 \le x_2 \} \cap \cdots \cap \{ X_N \le x_N \} ]$$$
(2) Joint PDF: $$$f_X(x) = \dfrac{\partial^N F_X(x)}{ \partial x_1 \partial x_2 \cdots \partial x_N }$$$
================================================================================

