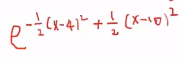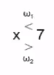Key points: - Statistical methods - Likelihood ratio test - Maximum likelihood estimation - Likelihood ================================================================================ pattern=statistical_decision_theory(data) ================================================================================ decision_function,decision_region,decision_boundary=likelihood_ratio_test() ================================================================================ estimated_prob_density_function=maximum_likelihood_estimation(data) ================================================================================ Likelihood: how much similar? LRT: test "similarity" by using "ratio" ================================================================================ * LRT: * You suppose you know probability density function of data * Now, you want to classify that data based on probability density function ================================================================================ * Classification example * You have data composed of weight values and height values * By using that data, create classifier model, * and classify given feature vector x composed of height and weight ================================================================================ * Method1 * Code posterior_prob_val_of_class1=posterior_prob_of_class1(feature_vec1) posterior_prob_val_of_class2=posterior_prob_of_class2(feature_vec1) posterior_prob_list=[posterior_prob_val_of_class1,posterior_prob_val_of_class2] idx_of_max=max(posterior_prob_list) selected_class=posterior_prob_list[idx_of_max] ================================================================================ * Method1 * Math Posterior prob = prior prob $$$\times$$$ likelihood $$$P(\omega_i|x) = P(\omega_i) \times P(x|\omega_i)$$$ * $$$P(\omega_i) \approx \frac{N_i}{N}$$$ $$$N$$$: number of samples $$$N_i$$$: number of samples resided in class $$$\omega_i$$$ If $$$N$$$ is enough bigger, $$$\frac{N_i}{N}$$$ becomes more similar to $$$P(\omega_i)$$$ * If P(\omega_1|x) > P(\omega_2|x), choose class $$$\omega_1$$$ else, choose class $$$\omega_2$$$ * Math notation for above sentence * Red square is likelihood ratio * You can classify class of feature vector based on likelihood ratio and prior probability ratio ================================================================================ * Example * 2 classes: $$$\omega_1$$$, $$$\omega_2$$$ * probability density function 1. Probability distribution of $$$\omega_1$$$ occuring $$$P(x|\omega_1)= \frac{1}{\sqrt{2\pi}} e^{\frac{1}{2} (x-4)^2}$$$ $$$N(\mu=4,\sigma=1)$$$ 2. 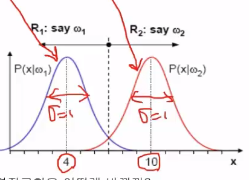Probability distribution of $$$\omega_2$$$ occuring $$$P(x|\omega_2)= \frac{1}{\sqrt{2\pi}} e^{\frac{1}{2} (x-10)^2}$$$ $$$N(\mu=10,\sigma=1)$$$ * Supposed condition: same prior probability $$$P(\omega_1)=P(\omega_2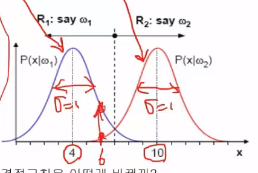)$$$ ================================================================================ * When you're given data of 6 * its class should be classified to $$$\omega_1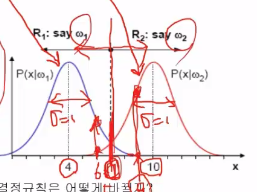$$$ ================================================================================ * Decision boundary: center vertical line, x=7 * It's "finding a classification boundary via LRT" ================================================================================ * Since you had supposed that $$$P(\omega_1)=P(\omega_2)$$$ * $$$\dfrac{\text{likelihood of class\;}$$$\omega_1$$$}{\text{likelihood of class\;}$$$\omega_2$$$}$$$ ================================================================================ * Above equation becomes simplified into ================================================================================ * Left fraction term can be simplified to 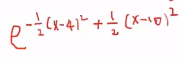================================================================================ * You apply log ================================================================================ * Finally, you get ================================================================================
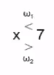