================================================================================
* Classifier can be considered as a tool which separate feature space into decision areas
* For example, separate feature height space.
 ================================================================================
When you use Bayes classifier with 2 classes,
your goal is to separate feature space $$$R$$$ into 2 spaces; $$$R_1$$$, $$$R_2$$$
based on their classes $$$\omega_1$$$, $$$\omega_2$$$
================================================================================
Error cases of above example are following
- Bayes classifier incorrectly says given feature vector x (which is in class of $$$\omega_1$$$) is involved in $$$R_2$$$
- Bayes classifier incorrectly says given feature vector x (which is in class of $$$\omega_2$$$) is involved in $$$R_1$$$
================================================================================
Above error cases are exclusive to each other, that is, $$$\text{case1} \cap \text{case2} = \phi$$$
So, you can use summation on probability values
$$$P[\text{error}] \\
=P[\text{error}|\omega_1]P[\omega_1]+P[\text{error}|\omega_2]P[\omega_2]+\cdots+P[\text{error}|\omega_i]P[\omega_i] \\
=\sum\limits_{i=1}^{C} P[\text{error}|\omega_i] P[\omega_i]$$$
================================================================================
$$$P[\text{error}|\omega_i] \\
= P[\text{choose } \omega_j|\omega_i] \\
= \int_{R_j} P(x|\omega_i)dx$$$
* $$$P[\text{error}|\omega_i]$$$: probability of error occuring when $$$\omega_1$$$ is given
* $$$P[\text{choose } \omega_j|\omega_i]$$$: probability of "$$$\text{choose} \; \omega_j$$$" occuring when $$$\omega_1$$$ is given
* $$$\int_{R_j} P(x|\omega_i)dx$$$: Sum of probability of x occuring in $$$R_i$$$ area when $$$\omega_i$$$ is given
================================================================================
================================================================================
When you use Bayes classifier with 2 classes,
your goal is to separate feature space $$$R$$$ into 2 spaces; $$$R_1$$$, $$$R_2$$$
based on their classes $$$\omega_1$$$, $$$\omega_2$$$
================================================================================
Error cases of above example are following
- Bayes classifier incorrectly says given feature vector x (which is in class of $$$\omega_1$$$) is involved in $$$R_2$$$
- Bayes classifier incorrectly says given feature vector x (which is in class of $$$\omega_2$$$) is involved in $$$R_1$$$
================================================================================
Above error cases are exclusive to each other, that is, $$$\text{case1} \cap \text{case2} = \phi$$$
So, you can use summation on probability values
$$$P[\text{error}] \\
=P[\text{error}|\omega_1]P[\omega_1]+P[\text{error}|\omega_2]P[\omega_2]+\cdots+P[\text{error}|\omega_i]P[\omega_i] \\
=\sum\limits_{i=1}^{C} P[\text{error}|\omega_i] P[\omega_i]$$$
================================================================================
$$$P[\text{error}|\omega_i] \\
= P[\text{choose } \omega_j|\omega_i] \\
= \int_{R_j} P(x|\omega_i)dx$$$
* $$$P[\text{error}|\omega_i]$$$: probability of error occuring when $$$\omega_1$$$ is given
* $$$P[\text{choose } \omega_j|\omega_i]$$$: probability of "$$$\text{choose} \; \omega_j$$$" occuring when $$$\omega_1$$$ is given
* $$$\int_{R_j} P(x|\omega_i)dx$$$: Sum of probability of x occuring in $$$R_i$$$ area when $$$\omega_i$$$ is given
================================================================================
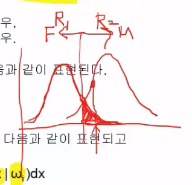 * Center vertical line: decision line
* Colored area: probability of error that $$$x$$$ is misclassified into $$$R_2$$$
* $$$\int_{R_j} P(x|\omega_i)dx$$$
================================================================================
In conclusion, probability of error on 2 classes is following
$$$P[\text{error}]=P[\omega_1] \int_{R_2} P(x|\omega_1) dx + P[\omega_2] \int_{R_1} P(x|\omega_2) dx$$$
================================================================================
Let's say
$$$\int_{R_2} P(x|\omega_1) dx = \epsilon_1$$$
$$$\int_{R_1} P(x|\omega_2) dx = \epsilon_2$$$
* Center vertical line: decision line
* Colored area: probability of error that $$$x$$$ is misclassified into $$$R_2$$$
* $$$\int_{R_j} P(x|\omega_i)dx$$$
================================================================================
In conclusion, probability of error on 2 classes is following
$$$P[\text{error}]=P[\omega_1] \int_{R_2} P(x|\omega_1) dx + P[\omega_2] \int_{R_1} P(x|\omega_2) dx$$$
================================================================================
Let's say
$$$\int_{R_2} P(x|\omega_1) dx = \epsilon_1$$$
$$$\int_{R_1} P(x|\omega_2) dx = \epsilon_2$$$
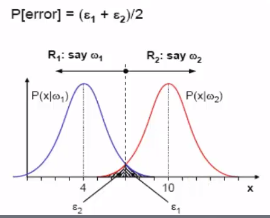 * Why do you divide by 2? Because you had supposed same prior probability
================================================================================
In any cases, minimum probability of error is obtained via LRT decision rule.
Minimum probability of error (which is obtained via LRT decision rule) is called
Bayes Error Rate, and classifier which uses Bayes Error Rate becomes best classifier.
================================================================================
* Why do you divide by 2? Because you had supposed same prior probability
================================================================================
In any cases, minimum probability of error is obtained via LRT decision rule.
Minimum probability of error (which is obtained via LRT decision rule) is called
Bayes Error Rate, and classifier which uses Bayes Error Rate becomes best classifier.
================================================================================


