This is note I wrote as I was take following lecture http://www.kocw.net/home/search/kemView.do?kemId=1189957 ================================================================================ * Summary for check the concept up. * What you wonder is "probability density function" * The data (which is assigned into each class) is generated via "probability density function" * If you can know "probability density function", then, you can make classify given data into best proper class ================================================================================ * So far, you just simply supposed that you know "probability density function" * But you should ask more intrinsic question like how you can know that "probability density function" itself? * To do that, you should inference best proper "probability density function" by using maximum likelihood estimation (which you learned from last lecture) ================================================================================ * But "inference" means "not precise one" * So, you should measure how "infereced probability density function" is accurate via values of "bias" and "variance" ================================================================================ * Bias is metric representing how near between "inference probability density function" and "real probability density function" 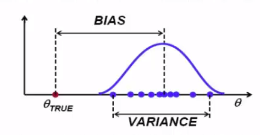* $$$\theta_{\text{TRUE}}$$$: true $$$\theta$$$ * High bias, more false in your inference * Curve means probability distribution of inferenced $$$\theta$$$ * Variance: how much of probability of inferenced $$$\theta$$$ varies whenever $$$\theta$$$ varies * Width of distribution ================================================================================ * Bias and variance have trade-off relationship * High bias, low variance ================================================================================ * Inference parameter $$$\mu$$$ via MLE is "unbiased inference" That is, inference value which is unbiased * $$$E[\hat{\mu}] = E \left[ \frac{1}{N} \sum\limits_{k=1}^{N} x_k \right] = \frac{1}{N} \sum\limits_{k=1}^{N} E[x_k]=\mu$$$ * Inference parameter $$$\sigma^2$$$ via MLE is "biased inference" That is, inference value which is biased * $$$E[\hat{\sigma}^2] = E \left[ \frac{1}{N} \sum\limits_{k=1}^{N} (x_k-\hat{\mu})^2 \right] = E \left[ \frac{1}{N} \sum\limits_{k=1}^{N} (x_k^2 - 2x_k\hat{\mu}+\hat{\mu}^2) \right]$$$ * If you divide by "N-1", it reduces bias toward 0 (better inference) especially when you have small N ================================================================================