This is note I wrote as I was take following lecture http://www.kocw.net/home/search/kemView.do?kemId=1189957 ================================================================================ Let's see "case 4" ================================================================================ Case 4: $$$\Sigma_i = \sigma^2_i I = \begin{bmatrix} \sigma_i^2&&0&&0\\0&&\sigma_i^2&&0\\0&&0&&\sigma_i^2 \end{bmatrix}$$$ * Each ith class has difference variance * Spread shape is same ================================================================================ What shape will classifying function have for this case 4? 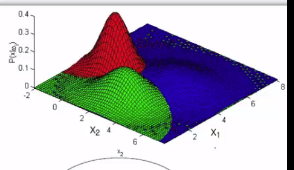$$$g_i(x) \\ = -\frac{1}{2} (x-\mu_i)^T \Sigma_i^{-1} (x-\mu_i) - \frac{1}{2} \log{(|\Sigma_i|)} + \log{(P(\omega_i))} \\ = -\frac{1}{2} (x-\mu_i)^T \sigma_i^{-2} (x-\mu_i) - \frac{1}{2}N \log{(\sigma_i^2)} + \log{(P(\omega_i))}$$$ * Above equation is i-dependent function ================================================================================ * Example $$$\mu_1=[3 \;\; 2]^T$$$ $$$\Sigma_1= \begin{bmatrix} 0.5&&0\\0&&0.5 \end{bmatrix}$$$ $$$\mu_2=[5 \;\; 4]^T$$$ $$$\Sigma_2= \begin{bmatrix} 1&&0\\0&&1 \end{bmatrix}$$$ $$$\mu_3=[2 \;\; 5]^T$$$ $$$\Sigma_3= \begin{bmatrix} 2&&0\\0&&2 \end{bmatrix}$$$ * Find "decision boundary" for data which has "3 classes", each class has 2 dimentions 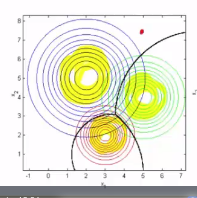================================================================================ * If you got new data point, that data point should be classified into what class (blue, green, red)? * Decision boundary shape is not linear (non linear decision boundary) 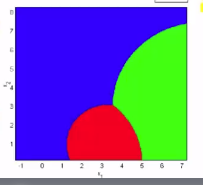================================================================================ * Zoom out to see entire view of classes ================================================================================ * Let's see general case * Case 5: $$$\Sigma_i \ne \Sigma_j$$$ * Each class has different variance * Distribution of height and weight will be different in its peak (mean) and width (or shape as variance) * Decision function $$$g_i(x)$$$ $$$g_i(x) \\ = -\frac{1}{2} (x-\mu_i)^T \Sigma_i^{-1} (x-\mu_i) - \frac{1}{2} \log{(|\Sigma_i|)} + \log{(P(\omega_i))}$$$ * Let's spread above equation $$$g_i(x) = x^TW_ix + w_i^Tx + w_{i0}$$$ * $$$W_t = -\frac{1}{2} \Sigma_i^{-1}$$$, matrix * $$$w_i = \Sigma_i^{-1}\mu_i$$$, vector * $$$w_{i0} = -\frac{1}{2} \mu_i^{T} \Sigma_{i}^{-1} \mu_i - \frac{1}{2} \log{(|\Sigma_i|)} + \log(P(\Omega_i))$$$, scalar * $$$x^TW_ix$$$, $$$w_i^Tx$$$, $$$w_{i0}$$$ are all scalars * You classify data by using scalar $$$g_i(x)$$$ * Shape is like $$$g_i(x) = ax^2 + bx + c$$$ ================================================================================ * Example $$$\mu_1=[3 \;\; 2]^T$$$ $$$\Sigma_1= \begin{bmatrix} 1&&-1\\-1&&2 \end{bmatrix}$$$ $$$\mu_2=[5 \;\; 4]^T$$$ $$$\Sigma_2= \begin{bmatrix} 1&&-1\\-1&&7 \end{bmatrix}$$$ $$$\mu_3=[2 \;\; 5]^T$$$ $$$\Sigma_3= \begin{bmatrix} 0.5&&0.5\\0.5&&3 \end{bmatrix}$$$ ================================================================================ * Find decision boundary for data which has 3 classes, 2 dim feature Each class' mean and covariance are given from above ================================================================================ * Distribution of each class data * Decision boundary ================================================================================ * 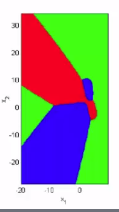Let's zoom out to view entire decision boundary ================================================================================ Summary * Bayes classifier is ultimately 2-order classifier ================================================================================ When following conditions are satisfied 1. all classes follow Gaussian distribution 2. all classes have same covariance 3. all classes have same prior probability it's case 3: $$$\Sigma_i=\Sigma=\begin{bmatrix} \sigma_1^2&&c_{12}&&c_{13}\\c_{12}&&\sigma_2^2&&c_{23}\\c_{13}&&c_{23}&&\sigma_3^2 \end{bmatrix}$$$ And you can use mahalanobis distance classifier as classification between given new vector and class areas $$$g_i(x) = -\frac{1}{2} (x-\mu_i)^T \Sigma_{i}^{-1}(x-\mu_i)$$$ $$$g_i(x)$$$ max = $$$-\frac{1}{2} (x-\mu_i)^T \Sigma_{i}^{-1}(x-\mu_i)$$$ minimum ================================================================================ When following conditions are satisfied 1. all classes follow Gaussian distribution 2. all classes have covariance which is proportional to identity matrix 3. all classes have same prior probability it's case 1: $$$\Sigma_i=\sigma^2 I =\begin{bmatrix} \sigma^2&&0&&0\\0&&\sigma^2&&0\\0&&0&&\sigma^2 \end{bmatrix}$$$ And you can use Euclidian distance classifier as classification between given new vector and class areas $$$g_i(x) = - \frac{1}{2\sigma^2} (x-\mu_i)^T(I)(x-\mu_i)$$$ $$$g_i(x)$$$ max = $$$- \frac{1}{2\sigma^2} (x-\mu_i)^T(I)(x-\mu_i)$$$ minimum ================================================================================