================================================================================
* You can use kernel to estimate PDF
================================================================================
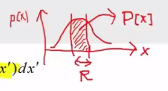
* Relationship between probability value and PDF
$$$P = \int_{R} p(x^{'}) dx^{'}$$$
* $$$P$$$: probability value
* $$$p(x^{'})$$$: PDF
 ================================================================================
* You get N number samples from population which is described by PDF p(x)
* You extract data N number of times
* $$$\{x_1,x_2,\cdots,x_N\}$$$
* $$$x_1$$$: height record from 100 people
* Probability of k number of vectors being involoved in region R
$$$P \cong \frac{k}{N}$$$
When $$$N \to \infty$$$, above P becomes more similar to $$$P = \int_{R} p(x^{'}) dx^{'}$$$
================================================================================
================================================================================
* You get N number samples from population which is described by PDF p(x)
* You extract data N number of times
* $$$\{x_1,x_2,\cdots,x_N\}$$$
* $$$x_1$$$: height record from 100 people
* Probability of k number of vectors being involoved in region R
$$$P \cong \frac{k}{N}$$$
When $$$N \to \infty$$$, above P becomes more similar to $$$P = \int_{R} p(x^{'}) dx^{'}$$$
================================================================================
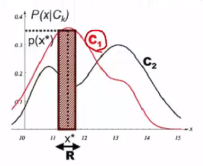 $$$C_1$$$: class 1, like height distribution
* If width is enough small, it becomes rectangle
* $$$P(x) \\
= \int_{x\in R} p(x) dx $$$
Standard way to calculate P
$$$ \cong p(x^{*})V$$$
Easy way, probability value * volume (or height in case of 2D)
================================================================================
1. $$$P(x) = \int_{R}p(x)dx \cong p(x^*)V$$$
2. $$$P(x) \cong \frac{k}{N}$$$
Then, you can write,
$$$\frac{k}{N} = p(x^*)V$$$
Conclusion: $$$p(x^*) \cong \frac{k}{NV}$$$
meaning: you can estimate p(x^*) by using N and V
* N: number of sample, each sample has D dimension
* k: number of frequency in given region R
* V: region R in case of 2D
================================================================================
If either $$$p(x^*)V$$$ or $$$\frac{k}{N}$$$ is precise,
$$$p(x^*) \cong \frac{k}{NV}$$$ becomes precise
* To make it more precise,
1. increase N
2. make V more narrow
================================================================================
Limitation
1. N number of samples can be $$$\infty$$$
2. If V is to narrow, it can have 0 sample
================================================================================
General equation to estimate PDF in non-parametric PDF estimation way
$$$p(x) \cong \frac{k}{NV}$$$
V: length (1D), region (2D), volume (3D), hypervolume (4D)
================================================================================
KDE (Kernel density estimation)
* Fix V and decide k
* Parzen window estimation:
- Use function $$$V_n=\frac{1}{\sqrt{n}}$$$ to decide $$$V_n$$$
by reducing region of V to estimate optimal density
k-NNR (k-nearest neighbor rule): does something by using nearest k data
* Fix k, decide V
* Fix $$$k_n=\sqrt{n}$$$ to be contained by V, and reduce V, and estimate optimal density
================================================================================
KDE method
$$$C_1$$$: class 1, like height distribution
* If width is enough small, it becomes rectangle
* $$$P(x) \\
= \int_{x\in R} p(x) dx $$$
Standard way to calculate P
$$$ \cong p(x^{*})V$$$
Easy way, probability value * volume (or height in case of 2D)
================================================================================
1. $$$P(x) = \int_{R}p(x)dx \cong p(x^*)V$$$
2. $$$P(x) \cong \frac{k}{N}$$$
Then, you can write,
$$$\frac{k}{N} = p(x^*)V$$$
Conclusion: $$$p(x^*) \cong \frac{k}{NV}$$$
meaning: you can estimate p(x^*) by using N and V
* N: number of sample, each sample has D dimension
* k: number of frequency in given region R
* V: region R in case of 2D
================================================================================
If either $$$p(x^*)V$$$ or $$$\frac{k}{N}$$$ is precise,
$$$p(x^*) \cong \frac{k}{NV}$$$ becomes precise
* To make it more precise,
1. increase N
2. make V more narrow
================================================================================
Limitation
1. N number of samples can be $$$\infty$$$
2. If V is to narrow, it can have 0 sample
================================================================================
General equation to estimate PDF in non-parametric PDF estimation way
$$$p(x) \cong \frac{k}{NV}$$$
V: length (1D), region (2D), volume (3D), hypervolume (4D)
================================================================================
KDE (Kernel density estimation)
* Fix V and decide k
* Parzen window estimation:
- Use function $$$V_n=\frac{1}{\sqrt{n}}$$$ to decide $$$V_n$$$
by reducing region of V to estimate optimal density
k-NNR (k-nearest neighbor rule): does something by using nearest k data
* Fix k, decide V
* Fix $$$k_n=\sqrt{n}$$$ to be contained by V, and reduce V, and estimate optimal density
================================================================================
KDE method
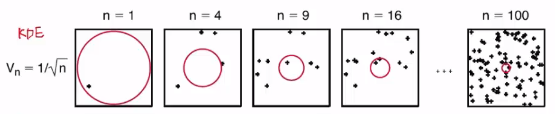 1. Fix volume $$$V_n$$$
2. Count k samples
n means number of sample
Each circle shows optimal size of circle wrt number of sample
================================================================================
k-NRR
1. Fix volume $$$V_n$$$
2. Count k samples
n means number of sample
Each circle shows optimal size of circle wrt number of sample
================================================================================
k-NRR




