================================================================================ * PCA: technique which reduces dimensionality of feature vector ================================================================================ * Curse of dimensionality: various problems as dimension goes higher in multivariate analysis ================================================================================ * Example * pattern recognition problem with 3 classes * method: - divide "feature space" into same sized 3 bins - count samples which are involved each bins - when unknown data is given, you classify that data into dominated bin's class (k-NNR driven Bayes classifier) ================================================================================ * Example * 3 classes * feature vector is 1 dimension 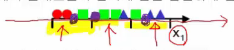* 1st bin : red dominant * 2nd bin : green dominant * 3rd bin : blue dominant * When you use 1D feature vector, if you divide 1 dimension axis into 3 bins, you can see classes are overlapped in too many places ================================================================================ You can use 2D feature vector $$$x=[x_1, x_2]$$$ When you use 2D feature vector, "feature space" becomes 2D, number of bin increases up to 9 bins (3*3) ================================================================================ You should choose either "constant density" or "constant number of example" * Constant density : 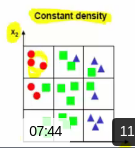* Each bin should have same or similar data 3 3 3 3 3 2 3 3 3 ================================================================================ * constant number of example : 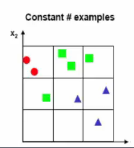2 2 1 1 1 1 0 0 1 * Meaning - If you have 0 data in some bins, there is no prob and statistical ways you can use ================================================================================ * You can use 3D feature vector, $$$x=[x_1,x_2,x_3]$$$ 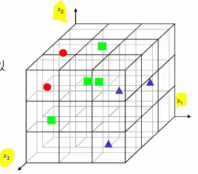* Number of bins: $$$27=3^{3}$$$ * constant density: 81=3*27 samples are required * constant number of example: * 9 data bin out of 81 bins * bin which has 1 data has no meaning * Sparse feature space problem ================================================================================ Issues of high dimensionality of feature vector * "Low performance of classification" due to "noise features" * "Slow" training and recognition speed * Needs more huge data for training for high dimensional feature vector ================================================================================ * Curse of the dimensionality ================================================================================ Solution for curse of the dimensionality * Use prior knowledge and domain knowledge * Increase smoothness of target function (or hypothesis function) * Reduce dimensionality of feature vector ================================================================================ * How to reduce dimensionality of feature vector - Feature selection - Feature extraction ================================================================================ * Feature selection : 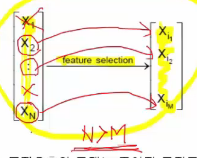* You select "partial features" from original feature vector * This is not much useful ================================================================================ * Feature extraction : * Code original_feature_vector=[x_1,x_2,...,x_N] extracted_feature_vector=feature_extraction_func(original_feature_vector) print(extracted_feature_vector) $$$[y_1,y_2,...,y_M]$$$ * Most information of original feature vector should be kept * feature_extraction_func = non-linear function or linear function (this is much used) ================================================================================ * Linear transformation $$$y=Wx$$$ $$$x$$$: original vector $$$y$$$: transformed vector $$$W$$$: transformation matrix ================================================================================ You can use PCA to find W