03_004_Eigenvector_Eigenvalue.html
=========================================================
matrix A (square matrix)
vector x $$$\neq$$$ 0
$$$x \in R^{n}$$$ (n-D real number vector)
if there is vector x which satisfies following relation :
(matrix A)(vector x)=(scalar value)(vector x)
$$$Ax=\lambda x$$$
then, you can call vector x as eigenvector (corresponding to $$$\lambda$$$) "of matrix A"
$$$\lambda$$$ : scalar value, eigenvalue of "matrix A"
=========================================================
example
$$$\begin{bmatrix} 2&3\\2&1 \end{bmatrix} \begin{bmatrix} 3\\2 \end{bmatrix} = \begin{bmatrix} 12\\8 \end{bmatrix} = 4 \begin{bmatrix} 3\\2 \end{bmatrix} $$$
$$$\begin{bmatrix} 2&3\\2&1 \end{bmatrix}$$$ : A
$$$\begin{bmatrix} 3\\2 \end{bmatrix}$$$ : x
4 : $$$\lambda$$$
=========================================================
induce steps
$$$Ax=\lambda x$$$
$$$Ax-\lambda x=0$$$
$$$(A-\lambda I)x=0$$$
then, $$$x=0$$$ or $$$(A-\lambda I)=0$$$
you choose $$$(A-\lambda I)=0$$$
Solving $$$(A-\lambda I)=0$$$ is equivalent to solving $$$|A-\lambda I|=0$$$
Therefore, you can call $$$|A-\lambda I|=0$$$ as characteristic equation of matrix A
Since $$$A-\lambda I$$$ is also matrix :
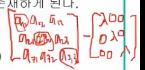 you can find its determinant
$$$(A-\lambda I)=0 \Rightarrow |A-\lambda I|=0 \Rightarrow \lambda^{N} + a_{1}\lambda^{N-1} + ... + a_{N-1}\lambda + a_{N}=0 $$$
A : nxn matrix
$$$\lambda$$$ : eigenvalue of A
set composed of all eigenvectors corresponding to eigenvalue $$$\lambda$$$ forms subspace of $$$R^{n}$$$ along with 0 vector
This subspace is called eigenspace of A
=========================================================
characteristic of eigenvalue and eigenvector
=========================================================
eigenvalue of diagonal matrix is its diagonal elements
=========================================================
eigenvalue of tri-matrix is its diagonal elements
you can find its determinant
$$$(A-\lambda I)=0 \Rightarrow |A-\lambda I|=0 \Rightarrow \lambda^{N} + a_{1}\lambda^{N-1} + ... + a_{N-1}\lambda + a_{N}=0 $$$
A : nxn matrix
$$$\lambda$$$ : eigenvalue of A
set composed of all eigenvectors corresponding to eigenvalue $$$\lambda$$$ forms subspace of $$$R^{n}$$$ along with 0 vector
This subspace is called eigenspace of A
=========================================================
characteristic of eigenvalue and eigenvector
=========================================================
eigenvalue of diagonal matrix is its diagonal elements
=========================================================
eigenvalue of tri-matrix is its diagonal elements
 =========================================================
If vector x is eigenvector of matrix A, kx is also eigenvector of matrix A
=========================================================
eigenvalue of A == eigenvalue of $$$A^{T}$$$
=========================================================
eigenvalue of $$$A = \lambda$$$
eigenvalue of $$$A^{-1} = \frac{1}{\lambda}$$$
=========================================================
eigenvalues of A : $$$\lambda_{1}, \lambda_{2}, ..., \lambda_{n}$$$
$$$\lambda_{1} \times \lambda_{2} \times ... \times \lambda_{n}$$$ = determinant of A
=========================================================
eigenvectors of each eigenvalue are linearly independent
diagonal matrix
$$$A = \begin{bmatrix} 1&0&0 \\ 0&2&0 \\ 0&0&3 \end{bmatrix}$$$
eigenvalues of A :
$$$\lambda_{1} = 1$$$
$$$\lambda_{2} = 2$$$
$$$\lambda_{3} = 3$$$
eigenvector of A :
$$$u_{\lambda_{1}} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} $$$
$$$u_{\lambda_{2}} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} $$$
$$$u_{\lambda_{3}} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $$$
$$$u_{\lambda_{1}}, u_{\lambda_{2}}, u_{\lambda_{3}}$$$ are linearly independent
=========================================================
eigenvectors of real number symmetric matrix are orthogonal to each others
=========================================================
eigenvalues of real number symmetric matrix are real number
=========================================================
if A is positive-definite matrix, all eigenvalues of A are positive
=========================================================
If vector x is eigenvector of matrix A, kx is also eigenvector of matrix A
=========================================================
eigenvalue of A == eigenvalue of $$$A^{T}$$$
=========================================================
eigenvalue of $$$A = \lambda$$$
eigenvalue of $$$A^{-1} = \frac{1}{\lambda}$$$
=========================================================
eigenvalues of A : $$$\lambda_{1}, \lambda_{2}, ..., \lambda_{n}$$$
$$$\lambda_{1} \times \lambda_{2} \times ... \times \lambda_{n}$$$ = determinant of A
=========================================================
eigenvectors of each eigenvalue are linearly independent
diagonal matrix
$$$A = \begin{bmatrix} 1&0&0 \\ 0&2&0 \\ 0&0&3 \end{bmatrix}$$$
eigenvalues of A :
$$$\lambda_{1} = 1$$$
$$$\lambda_{2} = 2$$$
$$$\lambda_{3} = 3$$$
eigenvector of A :
$$$u_{\lambda_{1}} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} $$$
$$$u_{\lambda_{2}} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} $$$
$$$u_{\lambda_{3}} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $$$
$$$u_{\lambda_{1}}, u_{\lambda_{2}}, u_{\lambda_{3}}$$$ are linearly independent
=========================================================
eigenvectors of real number symmetric matrix are orthogonal to each others
=========================================================
eigenvalues of real number symmetric matrix are real number
=========================================================
if A is positive-definite matrix, all eigenvalues of A are positive

