13-03 LDA(linear discriminant analysis)
=========================================================
$$$(\widetilde{\mu}_{1} - \widetilde{\mu}_{2})^{2} = (w^{T}{\mu}_{1}-w^{T}{\mu}_{2})^{2}$$$
$$${\mu}_{1}$$$ : average of class 1 data before projection
$$$\widetilde{\mu}_{1}$$$ : average of class 1 data after projection
$$$w^{T}$$$ : tranpose of transform matrix.
You can write this :
$$$(\widetilde{\mu}_{1} - \widetilde{\mu}_{2})^{2} = w^{T}({\mu}_{1}-{\mu_{2}})({\mu_{1}}-{\mu_{2}})^{T}w$$$
$$$(\widetilde{\mu_{1}} - \widetilde{\mu_{2}})^{2} = w^{T}S_{between-class\;scatter}w$$$
You can finally find following relation :
$$$\widetilde{S}_{between-class\;scatter} = (\widetilde{\mu}_{1} - \widetilde{\mu}_{2})^{2} = w^{T}S_{between-class\;scatter}w$$$
Therefore, you can replace target function J(w) notated with values after projection with target function J(w) notated with values before projection
$$$J(w) = \frac{|\widetilde{\mu}_{1}-\widetilde{\mu}_{2}|^{2}}{\widetilde{S}_{1}^{2}-\widetilde{S}_{2}^{2}} \Rrightarrow J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
You can achieve goal of optimization to maximize target function J(W) in respect to W by multiplying W
=========================================================
Fisher's linear discriminant equation :
$$$J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
You will go with above Fisher's linear discriminant equation
You goal is to find transform matrix W which maximizes above target function J(w) notated by $$$S_{between-class\;scatter}$$$ and $$$S_{within-class\;scatter}$$$
Shape of J(W) is proved as up-convex function
Therefore, at point which has 0 differentiation, you can say J(W) is maximum
2018-06-08 08-53-31.png
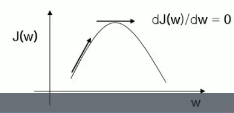 Your job is to find W which maximizes J(W)
In course of this job, you can find special characteristic
Using this special characteristic is called LDA
You should find W satisfying following formular
$$$\frac{d}{dw} \begin{vmatrix} J(w) \end{vmatrix} = \frac{d}{dw} \begin{vmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w} \end{vmatrix} = 0$$$
You can use following differentiation rule :
$$$\begin{pmatrix} \frac{f}{g} \end{pmatrix}' = \frac{f'g-g'f}{g^{2}}$$$
$$$\frac{d[w^{T}S_{between-class\;scatter}w]}{dw} [w^{T}S_{within-class\;scatter}w] - [w^{T}S_{between-class\;scatter}w] \frac{d[w^{T}S_{within-class\;scatter}w]}{dw} = 0$$$
You can simplify:
$$$2S_{between-class\;scatter}w[w^{T}S_{within-class\;scatter}w] - [w^{T}S_{between-class\;scatter}w] 2S_{within-class\;scatter}w = 0$$$
You divide both side by $$$w^{T}S_{within-class\;scatter}w$$$ then remove 2
$$$S_{between-class\;scatter}w [\frac{w^{T}S_{within-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}] - [\frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}] S_{w}w = 0$$$
You input :
$$$J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
then simplify :
$$$S_{between-class\;scatter}w-J(w)S_{within-class\;scatter}w = 0$$$
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = 0$$$
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = J(w)w$$$
This form is equal to $$$Au = \lambda u$$$
You this question becomes job of finding eigenvalue and eigenvector,
which means you will obtain similar result with PCA
$$$A = S_{within-class\;scatter}^{-1}S_{between-class\;scatter}$$$
You can say :
eigenvector $$$u = w$$$
eigenvalue $$$\lambda = J(w)$$$
In PCA, you first find covariance matrix, then, find $$$u\Lambda u^{T}$$$
In LDA, you first find $$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}$$$, then, find $$$u\Lambda u^{T}$$$
=========================================================
There is other LDA solution which doesn't perform eigenvalue analysis
Solution of generalized eigenvalue question $$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = J(w)w$$$ is as following :
You know :
$$$J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
Then, you input J(w) :
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w =\begin{bmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w} \end{bmatrix}w$$$
You can simplify :
$$$[w^{T}S_{between-class\;scatter}w] S_{within-class\;scatter}w = w^{T}S_{within-class\;scatter}w S_{between-class\;scatter}w$$$
$$$[w^{T}S_{between-class\;scatter}w] S_{within-class\;scatter}w = w^{T}S_{within-class\;scatter}w \alpha_{1}(\mu_{1}-\mu_{2}) $$$
where,
$$$S_{between-class\;scatter}w = (\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}w$$$ is vector which has same direction with $$$(\mu_{1}-\mu_{2})$$$
$$$S_{within-class\;scatter}w = \frac{w^{T}S_{within-class\;scatter}w}{w^{T}S_{between-class\;scatter}w} \alpha_{1} (\mu_{1}-\mu_{2})$$$
$$$S_{within-class\;scatter}w = \alpha_{2}\alpha_{1}(\mu_{1}-\mu_{2})$$$
$$$w = \alpha_{2}\alpha_{1} S_{within-class\;scatter}^{-1} (\mu_{1}-\mu_{2})$$$
Since size of vector W is not matter, you can ignore it :
$$$w^{*} = arg_{w}max \begin{bmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}} \end{bmatrix} = S_{within-class\;scatter}^{-1} (\mu_{1}-\mu_{2})$$$
=========================================================
Example question:
Find linear discriminant projection of following 2-D data
$$$\omega_{1} \; class : X_{1} = (x_{1}, x_{2}) = \{(4,1), (2,4), (2,3), (3,6), (4,4)\}$$$
$$$\omega_{2} \; class : X_{2} = (x_{1}, x_{2}) = \{(9,10), (6,8), (9,5), (8,7), (10,8)\}$$$
You perform dimensionality reduction by projecting data onto linear transform matrix w
After projection, you find transform matrix W which makes class of data seperated optimally
2018-06-08 09-00-11.png
Your job is to find W which maximizes J(W)
In course of this job, you can find special characteristic
Using this special characteristic is called LDA
You should find W satisfying following formular
$$$\frac{d}{dw} \begin{vmatrix} J(w) \end{vmatrix} = \frac{d}{dw} \begin{vmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w} \end{vmatrix} = 0$$$
You can use following differentiation rule :
$$$\begin{pmatrix} \frac{f}{g} \end{pmatrix}' = \frac{f'g-g'f}{g^{2}}$$$
$$$\frac{d[w^{T}S_{between-class\;scatter}w]}{dw} [w^{T}S_{within-class\;scatter}w] - [w^{T}S_{between-class\;scatter}w] \frac{d[w^{T}S_{within-class\;scatter}w]}{dw} = 0$$$
You can simplify:
$$$2S_{between-class\;scatter}w[w^{T}S_{within-class\;scatter}w] - [w^{T}S_{between-class\;scatter}w] 2S_{within-class\;scatter}w = 0$$$
You divide both side by $$$w^{T}S_{within-class\;scatter}w$$$ then remove 2
$$$S_{between-class\;scatter}w [\frac{w^{T}S_{within-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}] - [\frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}] S_{w}w = 0$$$
You input :
$$$J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
then simplify :
$$$S_{between-class\;scatter}w-J(w)S_{within-class\;scatter}w = 0$$$
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = 0$$$
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = J(w)w$$$
This form is equal to $$$Au = \lambda u$$$
You this question becomes job of finding eigenvalue and eigenvector,
which means you will obtain similar result with PCA
$$$A = S_{within-class\;scatter}^{-1}S_{between-class\;scatter}$$$
You can say :
eigenvector $$$u = w$$$
eigenvalue $$$\lambda = J(w)$$$
In PCA, you first find covariance matrix, then, find $$$u\Lambda u^{T}$$$
In LDA, you first find $$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}$$$, then, find $$$u\Lambda u^{T}$$$
=========================================================
There is other LDA solution which doesn't perform eigenvalue analysis
Solution of generalized eigenvalue question $$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w = J(w)w$$$ is as following :
You know :
$$$J(w) = \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w}$$$
Then, you input J(w) :
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter}w =\begin{bmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}w} \end{bmatrix}w$$$
You can simplify :
$$$[w^{T}S_{between-class\;scatter}w] S_{within-class\;scatter}w = w^{T}S_{within-class\;scatter}w S_{between-class\;scatter}w$$$
$$$[w^{T}S_{between-class\;scatter}w] S_{within-class\;scatter}w = w^{T}S_{within-class\;scatter}w \alpha_{1}(\mu_{1}-\mu_{2}) $$$
where,
$$$S_{between-class\;scatter}w = (\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}w$$$ is vector which has same direction with $$$(\mu_{1}-\mu_{2})$$$
$$$S_{within-class\;scatter}w = \frac{w^{T}S_{within-class\;scatter}w}{w^{T}S_{between-class\;scatter}w} \alpha_{1} (\mu_{1}-\mu_{2})$$$
$$$S_{within-class\;scatter}w = \alpha_{2}\alpha_{1}(\mu_{1}-\mu_{2})$$$
$$$w = \alpha_{2}\alpha_{1} S_{within-class\;scatter}^{-1} (\mu_{1}-\mu_{2})$$$
Since size of vector W is not matter, you can ignore it :
$$$w^{*} = arg_{w}max \begin{bmatrix} \frac{w^{T}S_{between-class\;scatter}w}{w^{T}S_{within-class\;scatter}} \end{bmatrix} = S_{within-class\;scatter}^{-1} (\mu_{1}-\mu_{2})$$$
=========================================================
Example question:
Find linear discriminant projection of following 2-D data
$$$\omega_{1} \; class : X_{1} = (x_{1}, x_{2}) = \{(4,1), (2,4), (2,3), (3,6), (4,4)\}$$$
$$$\omega_{2} \; class : X_{2} = (x_{1}, x_{2}) = \{(9,10), (6,8), (9,5), (8,7), (10,8)\}$$$
You perform dimensionality reduction by projecting data onto linear transform matrix w
After projection, you find transform matrix W which makes class of data seperated optimally
2018-06-08 09-00-11.png
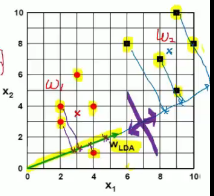
 You find variance and average within each class
$$$\mu_{1} = [3.00 3.60]$$$
$$$\mu_{2} = [8.40 7.60]$$$
average points are x marked
2018-06-08 09-01-30.png
You find variance and average within each class
$$$\mu_{1} = [3.00 3.60]$$$
$$$\mu_{2} = [8.40 7.60]$$$
average points are x marked
2018-06-08 09-01-30.png
 $$$S_{1} = \begin{bmatrix} 0.80&-0.04 \\ -0.04&2.60 \end{bmatrix}$$$
$$$S_{2} = \begin{bmatrix} 1.84&-0.04 \\ -0.04&2.64 \end{bmatrix}$$$
$$$S_{1}$$$ : covariance matrix (scatter) of data of $$$\omega_{1}$$$ class
between-class scatter(variance) :
$$$S_{between-class\;scatter} = (\mu_{1} - \mu_{2})(\mu_{1} - \mu_{2})^{T} = \begin{bmatrix} 29.16&21.60 \\ 21.60&16.00 \end{bmatrix}$$$
within-class scatter(variance) :
$$$S_{within-class\;scatter} = S_{1} + S_{2} = \begin{bmatrix} 2.64&-0.44 \\ -0.44&5.28 \end{bmatrix}$$$
You found all matrices you need
Now, you need to perform eigenvalue analysis
In case of $$$S_{within-class\;scatter}$$$, you can use program to find its inverse matrix
You can find LDA projection as solution of generalized eigenvalue question
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter} v = \lambda v \Rightarrow$$$
$$$|S_{within-class\;scatter}^{-1}S_{between-class\;scatter} - \lambda I | = 0 \Rightarrow$$$
$$$\begin{vmatrix} 11.89-\lambda&8.81 \\ 5.08&3.76-\lambda \end{vmatrix} = 0 \Rightarrow$$$
for eigenvalue $$$\lambda = 15.65$$$
You can input 15.65 :
$$$\begin{bmatrix} 11.89&8.81 \\ 5.08&3.76 \end{bmatrix} \begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} = 15.65 \begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} \Rightarrow$$$
for eigenvector $$$\begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} = \begin{bmatrix} 0.91\\0.39 \end{bmatrix}$$$
Let's try to draw this vector
This is vector what you want to find
$$$S_{1} = \begin{bmatrix} 0.80&-0.04 \\ -0.04&2.60 \end{bmatrix}$$$
$$$S_{2} = \begin{bmatrix} 1.84&-0.04 \\ -0.04&2.64 \end{bmatrix}$$$
$$$S_{1}$$$ : covariance matrix (scatter) of data of $$$\omega_{1}$$$ class
between-class scatter(variance) :
$$$S_{between-class\;scatter} = (\mu_{1} - \mu_{2})(\mu_{1} - \mu_{2})^{T} = \begin{bmatrix} 29.16&21.60 \\ 21.60&16.00 \end{bmatrix}$$$
within-class scatter(variance) :
$$$S_{within-class\;scatter} = S_{1} + S_{2} = \begin{bmatrix} 2.64&-0.44 \\ -0.44&5.28 \end{bmatrix}$$$
You found all matrices you need
Now, you need to perform eigenvalue analysis
In case of $$$S_{within-class\;scatter}$$$, you can use program to find its inverse matrix
You can find LDA projection as solution of generalized eigenvalue question
$$$S_{within-class\;scatter}^{-1}S_{between-class\;scatter} v = \lambda v \Rightarrow$$$
$$$|S_{within-class\;scatter}^{-1}S_{between-class\;scatter} - \lambda I | = 0 \Rightarrow$$$
$$$\begin{vmatrix} 11.89-\lambda&8.81 \\ 5.08&3.76-\lambda \end{vmatrix} = 0 \Rightarrow$$$
for eigenvalue $$$\lambda = 15.65$$$
You can input 15.65 :
$$$\begin{bmatrix} 11.89&8.81 \\ 5.08&3.76 \end{bmatrix} \begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} = 15.65 \begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} \Rightarrow$$$
for eigenvector $$$\begin{bmatrix} v_{1}\\v_{2} \end{bmatrix} = \begin{bmatrix} 0.91\\0.39 \end{bmatrix}$$$
Let's try to draw this vector
This is vector what you want to find


