<![CDATA[
% Lecture note from
% ]]> in clustering
In K-means clustering, K is manually set by human as hyperparameter
Is there machine learning tool which can automatically set most appropriate K of some data set?
Dirichlet Process is technique of setting most appropriate K
However, don't misunderstand that human task will disappear
Instead of human setting K, when machine tool setting K of each data, human sets kind of sensitivity of each data
then based on that sensitivity, machine tool sets K
Dirichlet Process is related to Dirichlet distribution
and related to methodology of clustering
% ===
% </xmp><img src=)
<![CDATA[
Let's first review Gaussian Mixture Model
K-means clustering is special case of Gaussian Mixture model
In plate notation (right bottom)
red circled x is data
$$$\mu$$$ and $$$\Sigma$$$ represent centers of cluster (centroids)
% ]]>
<![CDATA[
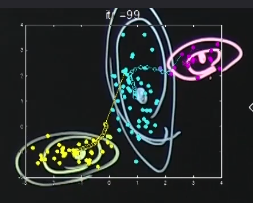Center dots are centroids
Ellipse contour lines represent probability distribution
3 clusters $$$\rightarrow$$$ 3 centroids
There are K number of $$$\mu$$$ and $$$\Sigma$$$
z is random variable which assigns each point (pixel?) into appropriate cluster
$$$\pi$$$ sets distribution dividing data,
for example, if there are 100 data,
$$$\pi$$$ sets distribution
where first cluster has 20, second cluster has 70, third cluster has 10
$$$\pi$$$ is kind of parameter value of multinomial distribution
Note that $$$\pi$$$, $$$\mu$$$, $$$\Sigma$$$ are not random variables but parameters
So, $$$\pi$$$, $$$\mu$$$, $$$\Sigma$$$ are not inside of plate (rectangle box, random variables are inside of rectangle box)
(Note that if $$$\pi$$$ is prior, this is Bayesian version GMM)
Parameter $$$\pi$$$ is vector and vector size is K
For example, you can write
$$$\pi = [0,2, 0.7, 0.1] $$$
Random variable z is multinomial distribution
% ===
% ]]>
<![CDATA[
There is K from $$$\pi$$$
And there is K from $$$\mu$$$ and $$$\Sigma$$$
Which K is first?
When you select $$$\pi$$$,
mixing coefficient $$$P(z_k)$$$ (line 5 from above picture) controls
$$$P(x|z)$$$ is probability likelyhood with respect to Mixture component (line 9 from above picture)
Both mixing coefficient $$$P(z_k)$$$ and mixture component $$$P(x|z)$$$ are related to K
$$$P(z_k)$$$ means there should be parameters (like 0.1, 0.7, 0.2) as much as K cluster (3 cluster)
$$$P(x|z)$$$ means there should be $$$\mu$$$, $$$\Sigma$$$ parameters to each cluster
So, "size of vector $$$\pi$$$" and "number of assignment of random variable z" can change number of centroids represented by $$$\mu$$$ and $$$\Sigma$$$
Distribution of selection variable z is related to number of cluster K
% ===
% ]]>
<![CDATA[
In last section, you learned size of selection variable z is important,
when setting number of cluster K
In summary,
Parameter $$$\pi$$$ affects selection random variable z
Distribution of z is multinomial distribution
You need to make size of choise of that multinomial distribution "free"
So, you can say parameter $$$\pi$$$ is parameter inside of above multinomial distribution
So, you need to be able to vary shape of above multinomial distribution
So, how to control multinomial distribution?
That (how to control multinomial distribution, by varying choice size) is required task
How to generate multinomial distribution?
It's almost not possible to manually change parameter $$$\pi$$$ to create multinomial distribution
So, you need to have automatical mechanism creating above multinomial distribution
Then, you need to have automatical mechanism which controls multinomial distribution
So, that mechanism creates parameter
and that mechanism varies size of generated parameter
and then finally that mechanism creates multinomial distribution
What is the method which creates parameters of multinomial distribution?
As that method, you can use Dirichlet distribution
% ===
So, let's review Dirichlet distribution
% ===
% ]]>
<![CDATA[
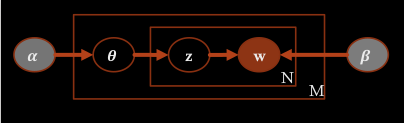This is LDA plate notation
LDA uses prior $$$\alpha$$$ to create $$$\theta$$$
By using $$$\theta$$$, perform assignment wrt z
Generative process: by using prior $$$\alpha$$$, create $$$\theta$$$
You pass $$$\alpha$$$ into Dirichlet distribution and get $$$\theta$$$
$$$\theta_i \sim Dir(\alpha)$$$
$$$\theta_i$$$ is proper form as parameter of multinomial distribution
$$$z_{i,l} \sim Mult(\theta_i)$$$
How is this possible?
When you see definition of Dirichlet distribution
you can see Dirichlet distribution is best tool to create parameter of multinomial distribution
Because
1. $$$x_1, ..., x_{K-1} > 0$$$
1. $$$x_1+...+_{K-1} < 1$$$
1. $$$x_k=1-x_1-...-x_{K-1}$$$
Above 3 ones satisfies probability axiom
What is $$$\alpha$$$ from $$$P(x_1,...,x_K|\alpha_1,...,\alpha_K)$$$?
$$$\alpha$$$ is space
when sample $$$x_1,...x_K$$$ which satisfy probability axiom is extracted from space
]]>