% https://www.youtube.com/watch?v=O75lE0HLu-A&index=24&t=0s&list=PLbhbGI_ppZIRPeAjprW9u9A46IJlGFdLn
% 002_Dirhichlet_Process_003.py
% ===
%  To understand Dirichlet Process,
you learned Gaussian Mixture model, general clustering model
You learned prior parameter is important
You could perform parameter sampling by using Dirichlet distribution
But still varying size is not possible
% ===
Let's define Dirichlet Process
$$$G|\alpha,H \sim DP(\alpha,H)$$$
G is being created
Last time, you created G with only $$$\alpha$$$
But this time, you will create G with $$$\alpha$$$ and H
H: base distribution, newly introduced one in DP
$$$\alpha$$$: concetration parameter, strength parameter (strength of prior)
parameter of Dirichlet distribution
% ===
$$$G|\alpha,H$$$ follows $$$DP(\alpha,H)$$$
Let's write above sentence in math form
G is generally not one number but like vector
because basically G will be used to create parameter of multinomial distribution
Sampled G: $$$G(A_1),...,G(A_r)$$$
when $$$\alpha$$$ and $$$H$$$ are given as condition
When you sample DP, you need distribution function
and you will that function as Dirichlet distribution
$$$(G(A_1),...,G(A_r))|\alpha,H \sim Dir(\alpha H(A_1),...,\alpha H(A_r))$$$
% ===
%
To understand Dirichlet Process,
you learned Gaussian Mixture model, general clustering model
You learned prior parameter is important
You could perform parameter sampling by using Dirichlet distribution
But still varying size is not possible
% ===
Let's define Dirichlet Process
$$$G|\alpha,H \sim DP(\alpha,H)$$$
G is being created
Last time, you created G with only $$$\alpha$$$
But this time, you will create G with $$$\alpha$$$ and H
H: base distribution, newly introduced one in DP
$$$\alpha$$$: concetration parameter, strength parameter (strength of prior)
parameter of Dirichlet distribution
% ===
$$$G|\alpha,H$$$ follows $$$DP(\alpha,H)$$$
Let's write above sentence in math form
G is generally not one number but like vector
because basically G will be used to create parameter of multinomial distribution
Sampled G: $$$G(A_1),...,G(A_r)$$$
when $$$\alpha$$$ and $$$H$$$ are given as condition
When you sample DP, you need distribution function
and you will that function as Dirichlet distribution
$$$(G(A_1),...,G(A_r))|\alpha,H \sim Dir(\alpha H(A_1),...,\alpha H(A_r))$$$
% ===
% 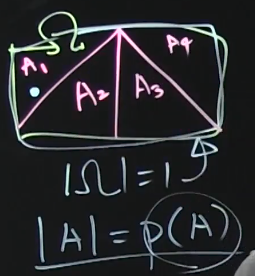 $$$A_1 \cap ... \cap A_r = \phi$$$
$$$A_1 \cup ... \cup A_r = \Omega$$$
It's that you insert PDF probability distribution
into Dirichlet distribution's parameter
Then, there is concetration $$$\alpha$$$ and
base distribution
So, with both which can vary, DP can vary
% ===
When you sample, what's expectaion?
Since you sample from Dirichlet distribution, expectaion will be center (green circle) and center will be base distribution
$$$E[G(A)]=H(A)$$$
Variance:
$$$V[G(A)] = \dfrac{H(A)(1-H(A))}{\alpha+1}$$$
H is distribution used to make parameter of Dirichlet distribution as base
to enable Dirichlet Process
% ===
Dirichlet process is managed by prior
Setting number of cluster is done by manipulating prior
You use likelihood on prior and you update posterior
$$$Posterior \propto Likelihood \times Prior$$$
Likelihood is about how many points are created in which region $$$(A_1, .., A_k)$$$
Prior is about how each region is divided
% ===
Let's expand more
$$$(G(A_1),...,G(A_r))|\theta_1,...,\theta_n, \alpha,H
\sim Dir(\alpha H(A_1)+n_1,...,\alpha H(A_r)+n_r)$$$
Condition $$$\alpha$$$, H still exist
$$$\theta_1, ..., \theta_n$$$: n number of trials
Each trial has each event
$$$n_k = |\{ \theta_i | \theta_i \in A_k, 1 \le i \le n \}|$$$
n: selectaion candidate
% ===
%
$$$A_1 \cap ... \cap A_r = \phi$$$
$$$A_1 \cup ... \cup A_r = \Omega$$$
It's that you insert PDF probability distribution
into Dirichlet distribution's parameter
Then, there is concetration $$$\alpha$$$ and
base distribution
So, with both which can vary, DP can vary
% ===
When you sample, what's expectaion?
Since you sample from Dirichlet distribution, expectaion will be center (green circle) and center will be base distribution
$$$E[G(A)]=H(A)$$$
Variance:
$$$V[G(A)] = \dfrac{H(A)(1-H(A))}{\alpha+1}$$$
H is distribution used to make parameter of Dirichlet distribution as base
to enable Dirichlet Process
% ===
Dirichlet process is managed by prior
Setting number of cluster is done by manipulating prior
You use likelihood on prior and you update posterior
$$$Posterior \propto Likelihood \times Prior$$$
Likelihood is about how many points are created in which region $$$(A_1, .., A_k)$$$
Prior is about how each region is divided
% ===
Let's expand more
$$$(G(A_1),...,G(A_r))|\theta_1,...,\theta_n, \alpha,H
\sim Dir(\alpha H(A_1)+n_1,...,\alpha H(A_r)+n_r)$$$
Condition $$$\alpha$$$, H still exist
$$$\theta_1, ..., \theta_n$$$: n number of trials
Each trial has each event
$$$n_k = |\{ \theta_i | \theta_i \in A_k, 1 \le i \le n \}|$$$
n: selectaion candidate
% ===
%  Definition of Dirichlet Process
$$$(G(A_1),...,G(A_r))|\alpha,H \sim DP(\alpha,H)$$$
$$$\sim Dir(\alpha H(A_1),...\alpha H(A_r))$$$
Posterior form of DP
$$$G|\theta_1,...,\theta_n,\alpha,H \sim
DP(\alpha+n,\dfrac{\alpha}{\alpha+n}H+\dfrac{n}{\alpha+n}
\dfrac{\sum_{i=1}^n \delta_{\theta_i}}{n})$$$
$$$\theta_1,...,\theta_n$$$: information from data
% ===
Definitioin of DP is done,
then how to realize (how to draw sample) definition of DP?
Above realize method is called "generation schemes" or "construction"
In case of DP, there are major 3 generation schemes (but 2 are very similar)
Stick Breaking Scheme
Polya Urn Scheme
Chinese Restraurant Process Scheme
Definition of Dirichlet Process
$$$(G(A_1),...,G(A_r))|\alpha,H \sim DP(\alpha,H)$$$
$$$\sim Dir(\alpha H(A_1),...\alpha H(A_r))$$$
Posterior form of DP
$$$G|\theta_1,...,\theta_n,\alpha,H \sim
DP(\alpha+n,\dfrac{\alpha}{\alpha+n}H+\dfrac{n}{\alpha+n}
\dfrac{\sum_{i=1}^n \delta_{\theta_i}}{n})$$$
$$$\theta_1,...,\theta_n$$$: information from data
% ===
Definitioin of DP is done,
then how to realize (how to draw sample) definition of DP?
Above realize method is called "generation schemes" or "construction"
In case of DP, there are major 3 generation schemes (but 2 are very similar)
Stick Breaking Scheme
Polya Urn Scheme
Chinese Restraurant Process Scheme


