This is personal study note
Copyright and original reference:
https://www.youtube.com/watch?v=EPlrYy9KuNU&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=58
================================================================================
Following algorithms are important to HMM
Forward probability
Backward probability
================================================================================
 $$$\pi$$$: parameter which is used to affect "first latent factor z"
$$$a$$$: transition probability of "state"
$$$b$$$: emission probability of "observation" from "state"
$$$X$$$: observation, dataset observed based on emission probability
================================================================================
Q1. Evaluation question
- When you have $$$\pi,a,b,X$$$
- you can create HMM structure
- From HMM, observation X is generated
- That observation is how much likelike observation? (evaluate that observation)
================================================================================
Q2. Decoding question
- When you have $$$\pi,a,b,X$$$
- you also have observation X, HMM structure M
- Find sequence Z of most likely latent factor z
- Suppose you have data (observation)
- Which latent factor z (or flow of z) can explain observation in best way?
================================================================================
Q3. Learning question
- When you have X (observation like professor's facial expression)
- You don't know parameters $$$\pi, a, b$$$
- Find parameters $$$\pi, a, b$$$ which maximize probability of given data X
- That is, inference parameters, learn parameters
================================================================================
In GMM, you also have only X (data)
And you found (inferenced) "mixture components", "probability of selecting mixtures"
This is "learning question"
================================================================================
$$$\pi$$$: parameter which is used to affect "first latent factor z"
$$$a$$$: transition probability of "state"
$$$b$$$: emission probability of "observation" from "state"
$$$X$$$: observation, dataset observed based on emission probability
================================================================================
Q1. Evaluation question
- When you have $$$\pi,a,b,X$$$
- you can create HMM structure
- From HMM, observation X is generated
- That observation is how much likelike observation? (evaluate that observation)
================================================================================
Q2. Decoding question
- When you have $$$\pi,a,b,X$$$
- you also have observation X, HMM structure M
- Find sequence Z of most likely latent factor z
- Suppose you have data (observation)
- Which latent factor z (or flow of z) can explain observation in best way?
================================================================================
Q3. Learning question
- When you have X (observation like professor's facial expression)
- You don't know parameters $$$\pi, a, b$$$
- Find parameters $$$\pi, a, b$$$ which maximize probability of given data X
- That is, inference parameters, learn parameters
================================================================================
In GMM, you also have only X (data)
And you found (inferenced) "mixture components", "probability of selecting mixtures"
This is "learning question"
================================================================================
 You can see Z
But Z should be marginalized out, but Z is invisible
So, alternatively, you should use "EM algorithm" also for HMM like GMM case
================================================================================
Decoding question: supervised learnig
- All parameters (as true dataset) are given
- Against given X dataset, find most likely parameter Z
Decoding question: unsupervised learnig
- like dynamic clustering
================================================================================
When you have "train data" (X and M), how can you know parameters $$$\pi,a,b$$$
---> Essentially it's counting method
You can see Z
But Z should be marginalized out, but Z is invisible
So, alternatively, you should use "EM algorithm" also for HMM like GMM case
================================================================================
Decoding question: supervised learnig
- All parameters (as true dataset) are given
- Against given X dataset, find most likely parameter Z
Decoding question: unsupervised learnig
- like dynamic clustering
================================================================================
When you have "train data" (X and M), how can you know parameters $$$\pi,a,b$$$
---> Essentially it's counting method
 ================================================================================
L: loaded dice (which is unfair dice)
F: fair dice
LLLLLFFF...: "latent factor z" which only casino dealer knows in his mind
1234253....: "observation x" you can see
dataset=create_dataset(above_information)
perform_supervised_learning(dataset)
================================================================================
$$$P(\text{L} \rightarrow \text{L}) = P(z_{t+1}=\text{L} | z_t = \text{L}) = a$$$
Transition probability: state L at time t ---> state L at time t+1
================================================================================
$$$ P(x_{t}=1 | z_t = \text{L}) = b$$$
observation number is 1 at time t = emit_observatioin(state is L at time t)
================================================================================
How to calculate probabilities a and b?
Use MLE, MAP by counting events
Then, you can find $$$\pi,a,b$$$ when you have X and M
================================================================================
What you saw:
- When dataset (X) and model M are given
- You can calculate parameters $$$\pi, a, b$$$
================================================================================
================================================================================
L: loaded dice (which is unfair dice)
F: fair dice
LLLLLFFF...: "latent factor z" which only casino dealer knows in his mind
1234253....: "observation x" you can see
dataset=create_dataset(above_information)
perform_supervised_learning(dataset)
================================================================================
$$$P(\text{L} \rightarrow \text{L}) = P(z_{t+1}=\text{L} | z_t = \text{L}) = a$$$
Transition probability: state L at time t ---> state L at time t+1
================================================================================
$$$ P(x_{t}=1 | z_t = \text{L}) = b$$$
observation number is 1 at time t = emit_observatioin(state is L at time t)
================================================================================
How to calculate probabilities a and b?
Use MLE, MAP by counting events
Then, you can find $$$\pi,a,b$$$ when you have X and M
================================================================================
What you saw:
- When dataset (X) and model M are given
- You can calculate parameters $$$\pi, a, b$$$
================================================================================
 ================================================================================
HMM can be "Bayesian network"
================================================================================
Suppose you have X (observation) and Z (latent factor or state)
$$$pi$$$, a, b = calculate_parameters(method=[MLE or MAP], observation=X, latent_factor=Z)
================================================================================
* If you have "full joint probability" like $$P(X,Z)$$, you can use "Bayesian network" in useful way
================================================================================
* In Bayesian network, you can use "factorization" by using "Bayesian network's topology"
================================================================================
* Factoize $$$P(X,Z)$$$
$$$P(X,Z) = \\
= P(x_1,\cdots,x_t,z_1,\cdots,z_t) \\
= P(z_1)\times P(x_1|z_1) \times P(z_2|z_1) \times P(x_2|z_2) \times P(z_3|z_2) \times P(x_3|z_3)$$$
$$$P(x_1|z_1)$$$: emission probability of observation $$$x_1$$$ from latent factor $$$z_1$$$
$$$P(z_2|z_1)$$$: transition probability from current latent factor $$$z_1$$$ to next latent factor $$$z_2$$$
================================================================================
Meaning:
$$$P(X,Z)$$$ is well factorized by "emission probability" and "transition probability"
================================================================================
You can write above notation using parameters $$$\pi,a,b$$$
$$$= \pi_{idx(z_1=1)} \times b_{idx(x_1=1),idx(z_1=1)} \times a_{idx(z_1=1),idx(z_2=1)} \times \cdots$$$
================================================================================
Suppose you know parameters $$$\pi,a,b$$$
When using L, probability of ocurring 1,2,3,4,5 is $$$\dfrac{1}{10}$$$
When using L, probability of ocurring 6 is $$$\dfrac{5}{10}$$$
$$$L\rightarrow L$$$: 70%
Casino dealer use 70% of L
================================================================================
Example of calculation "joint probability"
$$$P(166,LLL)$$$: how much likely is this situation?
$$$166$$$: observation
$$$LLL$$$: Z
$$$= \frac{1}{2} \times \frac{1}{10} \times \frac{7}{10} \times \frac{1}{2} \times \frac{7}{10} \times \frac{1}{2} \\$$$
$$$\frac{1}{2}$$$: $$$\pi$$$? (just randomly assume)
$$$\frac{1}{10}$$$: probability of "1" ocurring
$$$\frac{7}{10}$$$: use L from L
$$$ = 0.0061$$$
================================================================================
$$$P(166,FFF)$$$: how much likely is this situation?
$$$166$$$: observation
$$$LLL$$$: Z
$$$=\frac{1}{2} \times \frac{1}{6} \times \frac{1}{2} \times \frac{1}{6} \times \frac{1}{2} \times \frac{1}{6} \\$$$
$$$\frac{1}{2}$$$: initial state probability (just assume)
$$$\frac{1}{10}$$$: prob of "1" ocurring
$$$\frac{1}{2}$$$: use F from F
$$$=5.7870e-{04}$$$: very low probability
================================================================================
Conclusion:
Situation $$$P(166,FFF)$$$ is more likely
================================================================================
But possible scenario: $$$2^3$$$
2*2*2, x x x
You evaluated only 2 cases
But evaluating all cases takes much time
For this, you should use another method
================================================================================
================================================================================
HMM can be "Bayesian network"
================================================================================
Suppose you have X (observation) and Z (latent factor or state)
$$$pi$$$, a, b = calculate_parameters(method=[MLE or MAP], observation=X, latent_factor=Z)
================================================================================
* If you have "full joint probability" like $$P(X,Z)$$, you can use "Bayesian network" in useful way
================================================================================
* In Bayesian network, you can use "factorization" by using "Bayesian network's topology"
================================================================================
* Factoize $$$P(X,Z)$$$
$$$P(X,Z) = \\
= P(x_1,\cdots,x_t,z_1,\cdots,z_t) \\
= P(z_1)\times P(x_1|z_1) \times P(z_2|z_1) \times P(x_2|z_2) \times P(z_3|z_2) \times P(x_3|z_3)$$$
$$$P(x_1|z_1)$$$: emission probability of observation $$$x_1$$$ from latent factor $$$z_1$$$
$$$P(z_2|z_1)$$$: transition probability from current latent factor $$$z_1$$$ to next latent factor $$$z_2$$$
================================================================================
Meaning:
$$$P(X,Z)$$$ is well factorized by "emission probability" and "transition probability"
================================================================================
You can write above notation using parameters $$$\pi,a,b$$$
$$$= \pi_{idx(z_1=1)} \times b_{idx(x_1=1),idx(z_1=1)} \times a_{idx(z_1=1),idx(z_2=1)} \times \cdots$$$
================================================================================
Suppose you know parameters $$$\pi,a,b$$$
When using L, probability of ocurring 1,2,3,4,5 is $$$\dfrac{1}{10}$$$
When using L, probability of ocurring 6 is $$$\dfrac{5}{10}$$$
$$$L\rightarrow L$$$: 70%
Casino dealer use 70% of L
================================================================================
Example of calculation "joint probability"
$$$P(166,LLL)$$$: how much likely is this situation?
$$$166$$$: observation
$$$LLL$$$: Z
$$$= \frac{1}{2} \times \frac{1}{10} \times \frac{7}{10} \times \frac{1}{2} \times \frac{7}{10} \times \frac{1}{2} \\$$$
$$$\frac{1}{2}$$$: $$$\pi$$$? (just randomly assume)
$$$\frac{1}{10}$$$: probability of "1" ocurring
$$$\frac{7}{10}$$$: use L from L
$$$ = 0.0061$$$
================================================================================
$$$P(166,FFF)$$$: how much likely is this situation?
$$$166$$$: observation
$$$LLL$$$: Z
$$$=\frac{1}{2} \times \frac{1}{6} \times \frac{1}{2} \times \frac{1}{6} \times \frac{1}{2} \times \frac{1}{6} \\$$$
$$$\frac{1}{2}$$$: initial state probability (just assume)
$$$\frac{1}{10}$$$: prob of "1" ocurring
$$$\frac{1}{2}$$$: use F from F
$$$=5.7870e-{04}$$$: very low probability
================================================================================
Conclusion:
Situation $$$P(166,FFF)$$$ is more likely
================================================================================
But possible scenario: $$$2^3$$$
2*2*2, x x x
You evaluated only 2 cases
But evaluating all cases takes much time
For this, you should use another method
================================================================================
 - Now, your question is "observation X" is given
inference best likely latent factor Z
- Decoding question
================================================================================
Ultimately, in real case, you only know observation data X, you don't know latent factor Z
================================================================================
In GMM:
marginalize_out.wrt(Z)
you perform marginalize out wrt $$$Z$$$
$$$P(X|\theta) = \sum\limits_{z} P(X,Z|\theta)$$$
================================================================================
In HMM:
marginalize_out.wrt(Z)
In HMM, you can marginalize out wrt $$$Z$$$
$$$P(X|\pi,a,b) = \sum\limits_{Z} P(X,Z|\theta)$$$
================================================================================
$$$P(X) = \sum\limits_{Z} P(X,Z)$$$
# To remove Z
perform_summation(P(X,Z)).wrt(Z)
- Z is multiple random variables (multiple latent factors) = $$$\{z_1,z_2,\cdots,z_t\}$$$
================================================================================
Full joint distribution form
$$$= \sum\limits_{z_1} \cdots \sum\limits_{z_t} P(x_1,\cdots,x_t,z_1,\cdots,z_t)$$$
Perform factorization
$$$= \sum\limits_{z_1} \cdots \sum\limits_{z_t} \pi_{z_1} \prod_{t=2}^T a_{z_{t-1},z_t} \prod_{t=1}^{T} b_{z_t,x_t}$$$
================================================================================
Possible factorization even without constraint
$$$P(A,B,C) = P(A)P(B|A)P(C|A,B)$$$
================================================================================
By using above "factorization", "following complex form" should be changed into simple recursive form
- Now, your question is "observation X" is given
inference best likely latent factor Z
- Decoding question
================================================================================
Ultimately, in real case, you only know observation data X, you don't know latent factor Z
================================================================================
In GMM:
marginalize_out.wrt(Z)
you perform marginalize out wrt $$$Z$$$
$$$P(X|\theta) = \sum\limits_{z} P(X,Z|\theta)$$$
================================================================================
In HMM:
marginalize_out.wrt(Z)
In HMM, you can marginalize out wrt $$$Z$$$
$$$P(X|\pi,a,b) = \sum\limits_{Z} P(X,Z|\theta)$$$
================================================================================
$$$P(X) = \sum\limits_{Z} P(X,Z)$$$
# To remove Z
perform_summation(P(X,Z)).wrt(Z)
- Z is multiple random variables (multiple latent factors) = $$$\{z_1,z_2,\cdots,z_t\}$$$
================================================================================
Full joint distribution form
$$$= \sum\limits_{z_1} \cdots \sum\limits_{z_t} P(x_1,\cdots,x_t,z_1,\cdots,z_t)$$$
Perform factorization
$$$= \sum\limits_{z_1} \cdots \sum\limits_{z_t} \pi_{z_1} \prod_{t=2}^T a_{z_{t-1},z_t} \prod_{t=1}^{T} b_{z_t,x_t}$$$
================================================================================
Possible factorization even without constraint
$$$P(A,B,C) = P(A)P(B|A)P(C|A,B)$$$
================================================================================
By using above "factorization", "following complex form" should be changed into simple recursive form
 ================================================================================
First, you should consider "partial joint probability" than "full joint probability"
$$$P(x_1,\cdots,x_t,z_t^k=1)$$$
- $$$x_1,\cdots,x_t$$$: all observations are in the joint distribution
- $$$z_t^k=1$$$: only latent factor at time t is in the joint distribution
================================================================================
First, you should consider "partial joint probability" than "full joint probability"
$$$P(x_1,\cdots,x_t,z_t^k=1)$$$
- $$$x_1,\cdots,x_t$$$: all observations are in the joint distribution
- $$$z_t^k=1$$$: only latent factor at time t is in the joint distribution
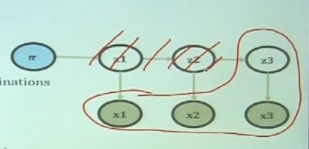 Remaining parts are marginalized out
================================================================================
From above equation, only one latent factor $$$z_{t-1}$$$ is introduced
Note that $$$z_{t-1}$$$ from $$$\sum\limits_{z_{t-1}}$$$
$$$\sum\limits_{z_{t-1}} P(x_1,\cdots,x_{t-1},x_t,z_{t-1},z_t^k=1)$$$
================================================================================
Remaining parts are marginalized out
================================================================================
From above equation, only one latent factor $$$z_{t-1}$$$ is introduced
Note that $$$z_{t-1}$$$ from $$$\sum\limits_{z_{t-1}}$$$
$$$\sum\limits_{z_{t-1}} P(x_1,\cdots,x_{t-1},x_t,z_{t-1},z_t^k=1)$$$
================================================================================
 Apply above "factorization" on it
================================================================================
Conclusion
Complicated form
$$$P(x_1,\cdots,x_t,z_t^k=1)$$$
into simplified form
$$$P(x_1,\cdots,x_t,z_t^k=1) = \alpha_t^k = b_{k,x_t} \sum\limits_{i} \alpha_{t-1}^i \alpha_{i,k}$$$
================================================================================
Apply above "factorization" on it
================================================================================
Conclusion
Complicated form
$$$P(x_1,\cdots,x_t,z_t^k=1)$$$
into simplified form
$$$P(x_1,\cdots,x_t,z_t^k=1) = \alpha_t^k = b_{k,x_t} \sum\limits_{i} \alpha_{t-1}^i \alpha_{i,k}$$$
================================================================================







