This is notes which I wrote as I was taking video lecture originated from
https://www.youtube.com/watch?v=UcrLWckwvI8&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=63
================================================================================
Forward sampling creates tons of cases which satisfy condition.
Rejection sampling is forward sample with several additional conditions.
================================================================================
Sampling-based methods need iteration for multiple sampling.
================================================================================
Suppose you want to know following probability by using rejection sampling.
$$$P(E=T|MC=T,A=F)=?$$$
================================================================================
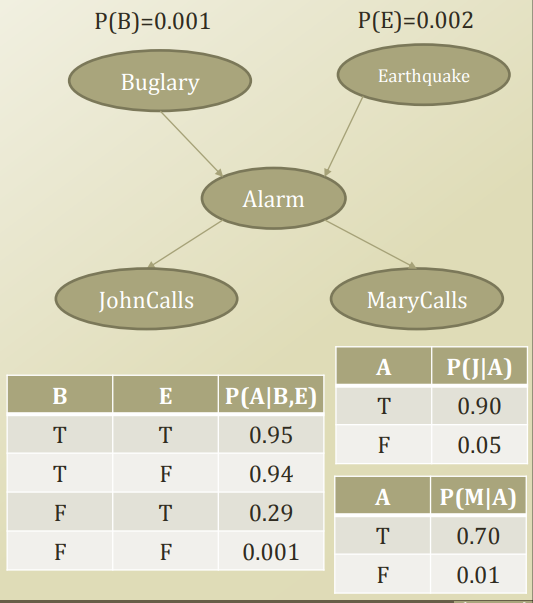 - Toss a dice at "Buglary"
Based on probability, some value will be assigned into "Buglary"
Suppose "false" is assigned into "Buglary"
- In the created topological order, toss the dice at "Earthquake".
And suppose you get "true" at "Earthquake".
- According to table, when B=F, E=T, alarm rings in 0.29 probability
Alarm|B=F,E=T -> true in 0.29 probability
But the problem is you already suppose A=F from your question $$$P(E=T|MC=T,A=F)$$$
- Above iteration is rejected.
- Go back to first step
================================================================================
- Suppose Alarm is false in above case.
- Suppose JohnCall is false.
- Suppose MaryCall is false, which doesn't satisfy your condition $$$P(E=T|MC=T,A=F)$$$
- So you reject abvoe iteration.
================================================================================
- Suppose MaryCall is true.
================================================================================
Then, all samples will satisfy given part $$$MC=T,A=F$$$ from $$$P(E=T|MC=T,A=F)$$$
================================================================================
$$$P(E=T|MC=T,A=F)=\dfrac{\text{Count cases where E=T,MC=T,A=F}}{\text{Number of samples}}$$$
================================================================================
- Toss a dice at "Buglary"
Based on probability, some value will be assigned into "Buglary"
Suppose "false" is assigned into "Buglary"
- In the created topological order, toss the dice at "Earthquake".
And suppose you get "true" at "Earthquake".
- According to table, when B=F, E=T, alarm rings in 0.29 probability
Alarm|B=F,E=T -> true in 0.29 probability
But the problem is you already suppose A=F from your question $$$P(E=T|MC=T,A=F)$$$
- Above iteration is rejected.
- Go back to first step
================================================================================
- Suppose Alarm is false in above case.
- Suppose JohnCall is false.
- Suppose MaryCall is false, which doesn't satisfy your condition $$$P(E=T|MC=T,A=F)$$$
- So you reject abvoe iteration.
================================================================================
- Suppose MaryCall is true.
================================================================================
Then, all samples will satisfy given part $$$MC=T,A=F$$$ from $$$P(E=T|MC=T,A=F)$$$
================================================================================
$$$P(E=T|MC=T,A=F)=\dfrac{\text{Count cases where E=T,MC=T,A=F}}{\text{Number of samples}}$$$
================================================================================
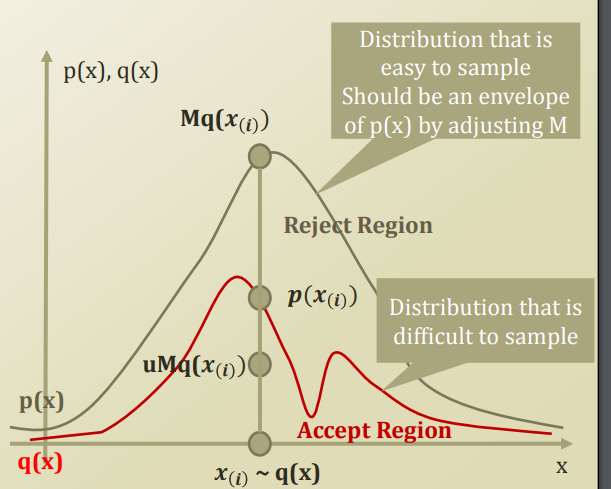 $$$x$$$: sample space
$$$q(x)$$$: Complicated probability distribution like "Mixture distribution"
which you want to do sampling from
It's what you want to analyze via sampling based inference.
It's difficult to calculate expectation, particular probability from that complicated distribution.
$$$p(x)$$$: simple probability distribution like "Normal distribution" which you know well.
You will perform sampling from it.
$$$p(x)$$$ envelops $$$q(x)$$$
================================================================================
Multiply M: $$$M \times q(x_{(x)})$$$, to create large distribution.
================================================================================
Suppose you sample some x in x axis from Normal distribution
Suppose $$$p(x_{(i)})=A, M \times q(x_{(i)})=B$$$
================================================================================
In conclusion, you will sample all values under $$$p(x)$$$
Then, by using $$$p(x_{(i)})=A, M \times q(x_{(i)})=B$$$
you create "reject region" and "accept region"
================================================================================
If $$$p(x)$$$ doesn't fully envelop $$$q(x)$$$, rejection sampling doesn't work correctly.
In that case, you can increase M, but as tradeoff, rejection region also grows,
resulting much more time consumption
================================================================================
$$$x$$$: sample space
$$$q(x)$$$: Complicated probability distribution like "Mixture distribution"
which you want to do sampling from
It's what you want to analyze via sampling based inference.
It's difficult to calculate expectation, particular probability from that complicated distribution.
$$$p(x)$$$: simple probability distribution like "Normal distribution" which you know well.
You will perform sampling from it.
$$$p(x)$$$ envelops $$$q(x)$$$
================================================================================
Multiply M: $$$M \times q(x_{(x)})$$$, to create large distribution.
================================================================================
Suppose you sample some x in x axis from Normal distribution
Suppose $$$p(x_{(i)})=A, M \times q(x_{(i)})=B$$$
================================================================================
In conclusion, you will sample all values under $$$p(x)$$$
Then, by using $$$p(x_{(i)})=A, M \times q(x_{(i)})=B$$$
you create "reject region" and "accept region"
================================================================================
If $$$p(x)$$$ doesn't fully envelop $$$q(x)$$$, rejection sampling doesn't work correctly.
In that case, you can increase M, but as tradeoff, rejection region also grows,
resulting much more time consumption
================================================================================
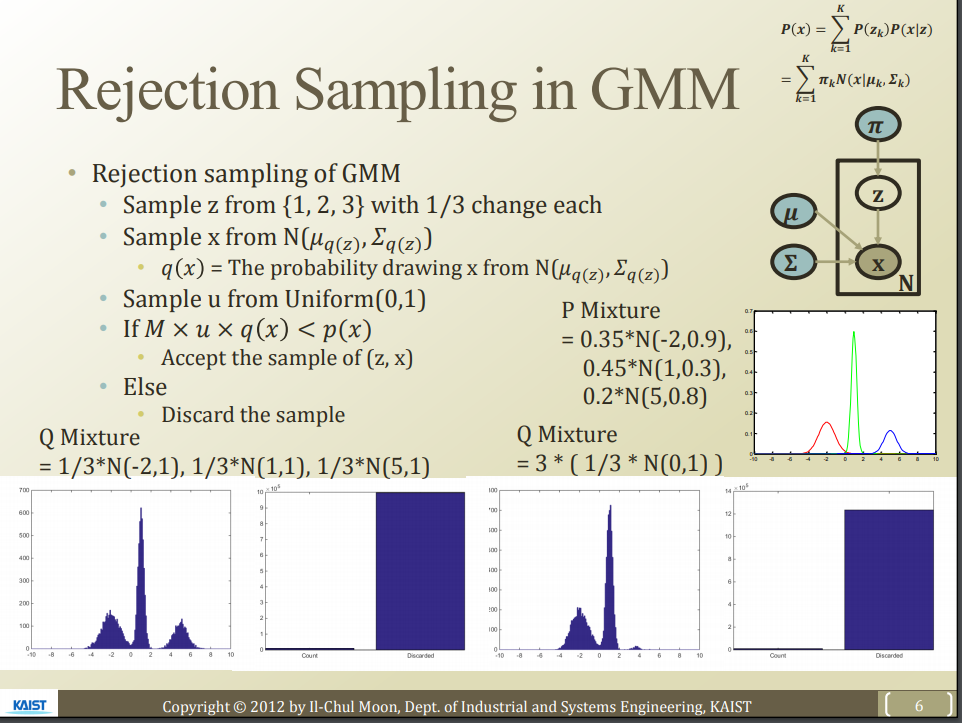 Perform sampling for mixture model by using rejection sampling.
================================================================================
Goal?
Perform sampling for mixture model by using rejection sampling.
================================================================================
Goal?
 ================================================================================
================================================================================
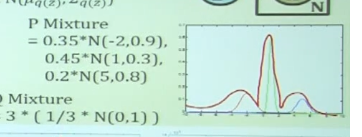
 3 Normal distributions
Multiply $$$\frac{1}{3}$$$ on them.
Reject center-colored region.
Perform sampling for GMM, blue-colored region.
================================================================================
3 Normal distributions
Multiply $$$\frac{1}{3}$$$ on them.
Reject center-colored region.
Perform sampling for GMM, blue-colored region.
================================================================================
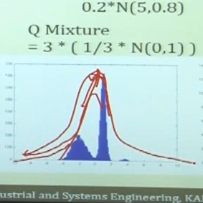 Use 1 normal distribution.
Unlike goal has right small peak
Use 1 normal distribution.
Unlike goal has right small peak
 it doesn't have right peak (unsampled in that region).
Solution:
1. use mixture Q model like first example
2. use large m than 3 to more envelop P-mixture (larger rejection region)
================================================================================
it doesn't have right peak (unsampled in that region).
Solution:
1. use mixture Q model like first example
2. use large m than 3 to more envelop P-mixture (larger rejection region)
================================================================================






