032. Week 06. Training, Testing, Regularization - 01. Overfitting, Underfitting



@
To understand training and testing, we need to understand bias and variance

@
We need to understand relationship between bias and variance in terms of trade-off

@
When we already have predicting model, how we to enhance performance of model

@
What does it mean by better machine learning?
It can mean accurate prediction result
In classification, accurate dicision
In regression, accurate prediction value

@
Suppose there is predicting model but always outputing "false"
And about data composed of 99 false and 1 true, predicting model can be said it can predict with 99\% accurately

So, we need good evalution and validation methodology for predicting model, output result, and even data set, etc

@
Training data is used to "parameter inference procedure"
We can also bring information from "prior knowledge" and "past experience"

@
The weak point of machine learning is that machine learning predicting model is only effective only under assumption that distribution of given data is not changed

If distribution of given data changed, we should make predicting model to learn newly

@
The reasons or conditions machine learning can't be effective in industry can be following
When domain changes
When current domain doesn't show enough variance, we can't guarantee future effectiveness of predicting model

@
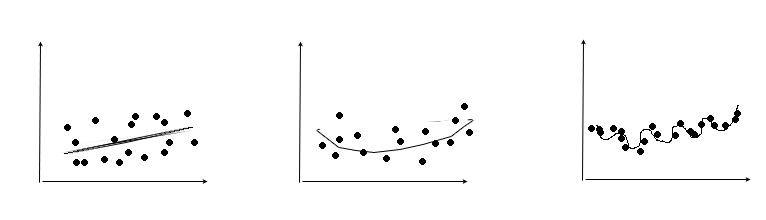
Suppose this scenario
1. You are given N points to train predicting model with those N points data
1. You are going to train simple polynomial regression function Y=F(x)
1. Y=F(x) can be linear or unlinear according to its undetermine degree

Now, consider following 3 F functions
Which one looks better?

@
1st one is one degree linear funtion (underfitting)
I didn't train some pattern
There are more area to train
The train is insufficient

2nd one is curved funtion (good one)

3rd one is high dgree function to fit every data point (overfitting)
This one will make least error in respect to train data set
But this one can make higher error in respect to unknow data than simply curven function

@
How to avoid "underfitting" and "overfitting" with some techniques?

As degree of hypothesis function increases, predicting model(hypothesis fuction) becomes complex
But complex model with high degree doesn't mean better predicting model

Then, question arises
Where should we stop increasing degree of hypothesis function?

Is there measurement to calculate complexity and generality of hypothesis function?

@
There is trade-off between complexity of model and generality of dataset
It means high generality of dataset brings low complexity of predicting model
It means low generality of dataset brings high complexity of predicting model