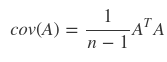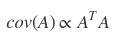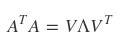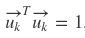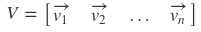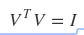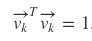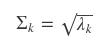================================================================================
https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/
/mnt/1T-5e7/mycodehtml/NLP/Latent_semantic_analysis/Ratsgo/main.html
================================================================================
Dimensionality reduction
- SVD
- PCA
================================================================================
SVD is used for LSA
================================================================================
PCA
- Preserve variance of data
- Find new axes (basies) which are perpendicular
new axes are independent
- Vectors in high dimension space into low dimension space
Example (vector in 3D space into vector in 2D space)
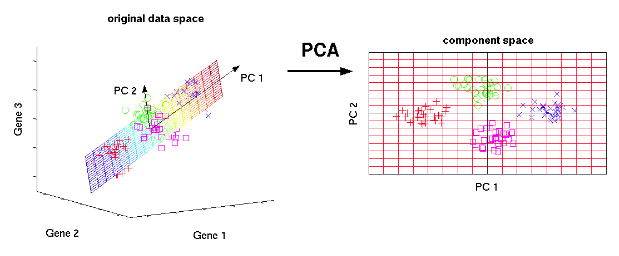 - Principal components: PC1, PC2
================================================================================
How to do PCA
- Your goal is to find new axes (new basies) which maximize "variance" of the data
- Find covariance matrix A from data matrix A
- Suppose each variable has 0 mean
- Covariance matrix A is calculated by
- Principal components: PC1, PC2
================================================================================
How to do PCA
- Your goal is to find new axes (new basies) which maximize "variance" of the data
- Find covariance matrix A from data matrix A
- Suppose each variable has 0 mean
- Covariance matrix A is calculated by
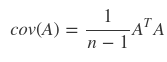
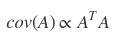 - Find new axes of PCA
- Perform "Eigen decomposition" on "covariance matrix A"
- Find new axes of PCA
- Perform "Eigen decomposition" on "covariance matrix A"
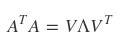 - $$$\Lambda$$$: matrix, diagonal elements are eigenvalues of covariance matrix
other locations are filled with 0
- $$$V$$$: matrix, column vectors are eigenvectors of covariance matrix $$$A^TA$$$
================================================================================
Diagonal elements of $$$\Lambda$$$:
Each variable (or each feature)'s variance from data matrix A
- Remember that your goal is to preserve "variance" of original data
- So, select some of large eigenvalues
- Find corresponding eigenvector from selected eigenvalue
- Perform projection (or linear transform) "original data" onto "eigenvector"
- Complete of PCA
================================================================================
Example
You have matrix of 100 dimension vectors
- Perform PCA
- Selcted 2 largest eigenvalues
- Perform projection (or linear transform) by using corresponding eigenvector
- You can get matrix of 2 dimension vectors
================================================================================
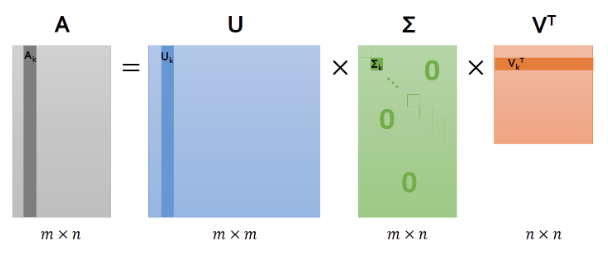
Lesson on SVD
Matrix A: (m,n)
A is decomposed into $$$U \Sigma V^T$$$
- $$$\Lambda$$$: matrix, diagonal elements are eigenvalues of covariance matrix
other locations are filled with 0
- $$$V$$$: matrix, column vectors are eigenvectors of covariance matrix $$$A^TA$$$
================================================================================
Diagonal elements of $$$\Lambda$$$:
Each variable (or each feature)'s variance from data matrix A
- Remember that your goal is to preserve "variance" of original data
- So, select some of large eigenvalues
- Find corresponding eigenvector from selected eigenvalue
- Perform projection (or linear transform) "original data" onto "eigenvector"
- Complete of PCA
================================================================================
Example
You have matrix of 100 dimension vectors
- Perform PCA
- Selcted 2 largest eigenvalues
- Perform projection (or linear transform) by using corresponding eigenvector
- You can get matrix of 2 dimension vectors
================================================================================
Lesson on SVD
Matrix A: (m,n)
A is decomposed into $$$U \Sigma V^T$$$
 ================================================================================
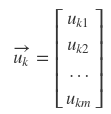
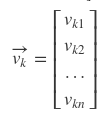
Column vectors in U and V are called "singular vector"
All singular vectors have "perpendicular characteristic"
================================================================================
Column vectors in U and V are called "singular vector"
All singular vectors have "perpendicular characteristic"


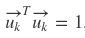
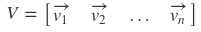
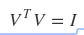
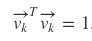 ================================================================================
Singular value of matrix $$$\Sigma$$$ $$$\ge$$$ 0
Singular value of matrix $$$\Sigma$$$ are arrange in descending order
kth diagonal element of $$$\Sigma$$$
$$$= \sqrt{\text{kth eigenvalue of matrix A}}$$$
================================================================================
Singular value of matrix $$$\Sigma$$$ $$$\ge$$$ 0
Singular value of matrix $$$\Sigma$$$ are arrange in descending order
kth diagonal element of $$$\Sigma$$$
$$$= \sqrt{\text{kth eigenvalue of matrix A}}$$$
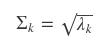 ================================================================================
Compare SVD with PCA
Perform squre on A
================================================================================
Compare SVD with PCA
Perform squre on A
 $$$\Sigma$$$: diagonal elements are "eigenvalues of mat A"
other elements are 0
$$$\text{Diagonal_matrix}^2$$$ = square of elements
$$$\Sigma^2 = \text{eigenvalue of mat A}$$$
But $$$ \text{eigenvalue of A} = \sqrt{\text{eigenvalue of A}}$$$
Therefore, $$$\Sigma^2 = \Lambda$$$
$$$\Lambda$$$ is composed of eigenvalue of $$$A^TA$$$
================================================================================
$$$\Sigma$$$: diagonal elements are "eigenvalues of mat A"
other elements are 0
$$$\text{Diagonal_matrix}^2$$$ = square of elements
$$$\Sigma^2 = \text{eigenvalue of mat A}$$$
But $$$ \text{eigenvalue of A} = \sqrt{\text{eigenvalue of A}}$$$
Therefore, $$$\Sigma^2 = \Lambda$$$
$$$\Lambda$$$ is composed of eigenvalue of $$$A^TA$$$
================================================================================

 ================================================================================
LSA
- There are 3 documents
doc1: I go to school
doc2: Mary go to school
doc3: I like Mary
- You can create Term-Document-Matrix
doc1 doc2 doc3
I 1 0 1
go 1 1 0
to 1 1 0
school 1 1 0
Mary 0 1 1
like 0 1 1
- LSA:
- You perform SVD on the input data: Term-Document-Matrix or Window-Based_co_occurrence
- You reduce the dimensionality of input data
- You increate computational efficiency
- You extract latent semantic from input data
================================================================================
LSA
- There are 3 documents
doc1: I go to school
doc2: Mary go to school
doc3: I like Mary
- You can create Term-Document-Matrix
doc1 doc2 doc3
I 1 0 1
go 1 1 0
to 1 1 0
school 1 1 0
Mary 0 1 1
like 0 1 1
- LSA:
- You perform SVD on the input data: Term-Document-Matrix or Window-Based_co_occurrence
- You reduce the dimensionality of input data
- You increate computational efficiency
- You extract latent semantic from input data