5. Transform the timespace(about special relativity theory)
@
특수상대성이론 : 시간과 공간에 대한 인류의 사고를 근본적으로 바꾼 과학적 혁명이다.
광속 불변의 법칙에 입각하여 시간과 공간의 변환에 대한 이론이다.
아인슈타인 맨 처음 독일어로 쓴 논문은 1905 On the electodynamics of moving bodies. 전자동역학시스템에있어서 움직이는 물체에 관하여 이다.
논문을 보면
시간과 공간, 즉, 움직이는 시스템하고 정지하는 시스템의 관계에 있어서 로렌츠 변환을 보여주는 것이다.
중간에 보면,
두 속도의 가산이 갈릴레이 가산 법칙과 다르다. 광속 불변의 법칙이 증명되는 속도 가산의 법칙과 공식을 보여준다.
@
아인슈타인의 특수상대성이론이 적용되는 것은 관성계(등속운동시스템)이다.
하지만, 엄밀하게 말하면 지구에서 등속운동시스템은 찾아보기 어렵다. 지구의 마찰 등 여러요인에 의해 대부분 가속도운동을 하게된다. 아인슈타인이 말하는 등속운동시스템의 정확한 예시는 진공을 달리는 빛의 움직임, 우주공간에서의 자유유영 등 이다.
이러한 등속운동시스템, 이른바 관성계에 있어서 시간과 공간의 변환 법칙들을 아인슈타인은 유도하였다.
@
인공위성은 원운동을 하니까 엄밀히 말해서 가속운동이다. 이런 인공위성이 지구에 중력이 없다면 영원한 등속도 운동을 하게된다. 우주선에서 외부를 볼수 없을때 등속운동한다면 움직이는지 정지하는지 아는것이 원천적으로 불가능하다는 것이 특수상대성이론의 중요한 결론이다.
@
이러한 특수상대성이론의 수학적 배경인 시간과 공간의 변환에 관한 로렌츠 변환에 대해서 알아보자.
ce798115-792c-47e3-a283-b6b78fdcecb9
출발은, 어떤시스템이 x,y,z 좌표로 표시되는 시스템이라는 가정이다. 이러한 시스템에 오버랩되게 또하나의 좌표 시스템이 있다고 해보자. 그 좌표 시스템을 $\bar{x}, \bar{y}, \bar{z}$ 라고 하자. 이 bar 가 붙은 시스템의 원점에서 빛이 켜졌다고 상상해보자.
그 후에 이 두 시스템은 랜턴이 없는 정지시스템과 이것에 대해서 속도 v로 움직이는 bar 가 붙은 랜턴이 있는 시스템을 상정해 볼 수 있다.
이 두 시스템에 있어서 광원이 퍼져나가는 거리, 간격을 수식으로 표현하면 $x^{2}+y^{2}+z^{2}-c^{2}t^{2}$ 이 된다. 4차원 시공이기 때문에 거리라고 하지 않고 interval(간격) 이라고 한다. 이것이 bar 가 붙은 시스템의 간격과 같은 값으로 일정하다. $x^{2}+y^{2}+z^{2}-c^{2}t^{2} = \bar{x^{2}}+\bar{y^{2}}+\bar{z^{2}}-\bar{c^{2}t^{2}}$
특수상대성이론에서 가장 중요한 것은 광속 불변의 원칙이다. 이게 무슨의미냐면 위 수식에서 bar 가 안붙은 시스템에서의 광속이나 거기에 대해서 등속도로 움직이는 bar가 붙은 시스템에서의 빛의 속도는 같다 라는 것이다.
그리고 수학적 간편을 위해서 나아가는 방향을 x축으로 두면 진행하는 방향과 수직인 y방향과 z방향은 양 시스템에서 같다고 볼수 있으니까 이 수식에서 제외를 할 수 있다. 그래서 x축만 고려한 간략한 시스템은
$x^{2}-c^{2}t^{2}=\bar{x^{2}}-c^{2}t^{2}$ 이라고 할 수 있다.
여기에서 T 이라는 새로운 변수를 도입한다. T=iCt 라고 두고 변환을 해보면, $t=\frac{T}{iC}$ 라고 볼 수 있으므로
$x^{2}-c^{2}t^{2}=\bar{x^{2}}-c^{2}t^{2}$
우측에서 T는 bar가 붙는다.
$x^{2}-c^{2}(\frac{T}{iC})^{2}=\bar{x^{2}}-c^{2}(\frac{\bar{T}}{iC})^{2}$
전개하면 $i^{2}=-1$ 이므로,
$x^{2}+T^{2}=\bar{x^{2}}+\bar{T^{2}}$
시간과 공간에 대한 위 수식 관계를 만족하는 변환이 로렌츠 변환이다.
이러한 변환 법칙은 크기가 일정한 회전좌표시스템에 해당된다. 회전변환이 위 변환을 만족하는 대표적인 변환이다.
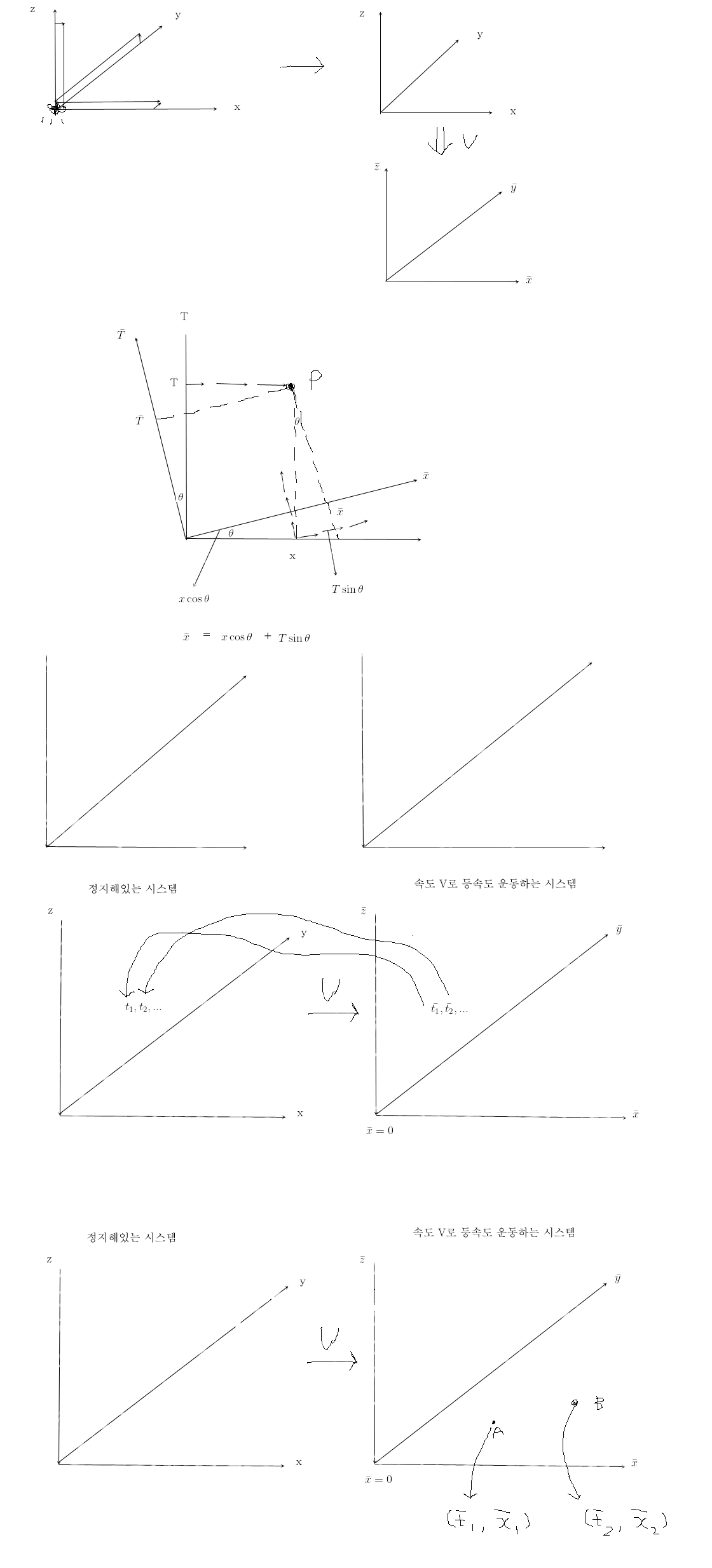
이 변환 시스템을 좌표로 표시하면 임의의 각도 $\theta$ 로 회전을 시킨다. 그럼 $\bar{T}$ 가 되고 x를 회전한축이 $\bar{x}$ 가 된다. bar 없는 좌표시스템과 bar있는 좌표시스템, 두 좌표 시스템에서 임의의 한 점 P 를 표현해 보자. P를 x와 T 시스템으로 표현해보면 x와 T가 된다. 그리고 동일한 점을 bar 가 붙은 좌표시스템으로 표현해보자. $\bar{T}$ 가 되고 $\bar{x}$ 가 된다. 보조 축을 그리고 $\theta$ 를 표시해 본다.
그러면 $\bar{x}=x\cos{\theta}+T\sin{\theta}$ 이다.
$\bar{T}$ 는 전체인 $T\cos{\theta}$ 에다가 $x\sin{\theta}$ 를 빼주면 된다.
따라서, 위 수식과 형태를 맞추기 위해서 다음과 같이 쓸수 있다.
$\bar{T} = -x\sin{\theta} + T\cos{\theta}$
정리하면,
$\bar{x}=x\cos{\theta}+T\sin{\theta}$
$\bar{T} = -x\sin{\theta} + T\cos{\theta}$
인데, 전형적인 회전변환에 관한 수식이 된다.
우리가 익히 알고있는 $\cos^{2}{\theta}+\sin^{2}{\theta} = 1$ 을 양변을 $\cos^{2}{\theta}$ 로 나눠본다.
$\frac{\cos^{2}{\theta}}{\cos^{2}} + \frac{\sin^{2}{\theta}}{\cos^{2}} = \frac{1}{\cos^{2}}$
$1 + \tan^{2}{\theta} = \frac{1}{\cos^{2}}$
양변 루트를 씌우면,
$\cos{\theta} = \frac{1}{\sqrt{1+tan^{2}{\theta}}}$ 가 된다.
@
우리가 풀어봐야할 시스템을 다시그려보자. 정지시스템인 K시스템. 거기에 대해서 등속도 V로 움직이는 bar 가 붙은 시스템. 우리가 고려하는 첫번째 포인트는 원점이다. 원점은 bar 시스템에서 표현하면 $\bar{x}=0$ 인 포인트이다. bar 가 붙은 시스템의 원점을 정지한 시스템에서 봤을때, 표현하면, 원점이 움직이는 x는 vt 가 된다.
이러한 내용을 아래의 수식에 넣어본다.
$\bar{x}=x\cos{\theta}+T\sin{\theta}$
$\bar{T}=-x\sin{\theta}+T\cos{\theta}$
$\bar{x}=0$ 이므로
$0=x\cos{\theta}+T\sin{\theta}$
$x\cos{\theta}=-T\sin{\theta}$
$x=-T\tan{\theta}$
$\tan{\theta}=-\frac{x}{T}$
T=iCt, x=vt 이므로
$\tan{\theta}=-\frac{vt}{iCt}$
$-1=i^{2}$ 이므로
$\tan{\theta}=\frac{iv}{C}$
위에서 구한 $\tan{\theta}$ 를 아래 수식에 대입한다.
$\cos{\theta}=\frac{1}{\sqrt{1+\tan^{2}{\theta}}}$
$\cos{\theta}=\frac{1}{\sqrt{1+(1+(\frac{iV}{C})^{2})}}$
그러면 그 유명한 $\Gamma$ factor 가 나온다.
$\cos{\theta}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}$
위수식을 우리가 구했던 아래의 회전변환 수식에 집어넣어준다.
$\cos{\theta}=\frac{1}{\sqrt{1+\tan^{2}{\theta}}}$
$\cos{\theta}=\frac{1}{\sqrt{1+(1+(\frac{iV}{C})^{2})}}$
$\cos{\theta}=\frac{1}{\sqrt{1+\tan^{2}{\theta}}}$ 를 아래와같이 변형시킨다.
$\bar{x}=\cos{\theta}(x+\bar{T}sin{\theta})$
위 $\cos{\theta}$ 를 대입한다.
$\bar{x}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}} (x+\bar{T}sin{\theta})$
$T=iCt, \tan{\theta}=\frac{iV}{C}$ 를 대입하면,
$\bar{x}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}} (x+iCt\frac{iV}{C})$
$\bar{x}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}} (x-Vt)$
위 수식의 의미는, $\bar{x}$ 는 bar 가 안붙은 x 와 t 로 좌표변환이 되는 것이다.
@
동일하게, $\bar{T}$ 를 정지시스템에서 표시해보면, 그러기 위해 $cos{\theta}$ 로 뽑아내면
$\bar{T}=-x\sin{\theta}+T\cos{\theta}$
$\bar{T}=\cos{\theta}(-x\tan{\theta}+T)$
$\cos{\theta}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}$ 이므로
$\bar{T}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}(-x\tan{\theta}+T)$
$\tan{\theta}=\frac{iv}{C}, T=iCt$ 이므로
$\bar{T}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}(-x\frac{iV}{C}+iCt)$
T=iCt 를 이용한다? 잘 이해 안됨.
$\bar{T}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}(-x\frac{iV}{C}+iCt)=iC\bar{t}$
양쪽에 iC로 나눠주면,
$\bar{t}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}} (-iCt\frac{1}{iC}-x\frac{iv}{C} \frac{1}{iC})$
$\bar{t}=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}} (t-\frac{V}{C^{2}}x)$
정지한 시스템에서 속도 V로 움직이는 시스템을 정지한 시스템으로 변환하는 관계식이다.
@
로렌츠 변환의 단측변환을 구해보았다. 등속도 운동 시스템에서 시간과 공간이 표현되는 방식이다.
bar 가 안붙은 시스템을 표현할 때는 속도만 V대신 -V를 넣어주면 된다. 상대적으로 등속운동할때 내가 정지해있고 대상이 움직인다고 해도되고 대상이 정지해있을때 내가 반대속도로 움직인다고 해도 동일하게 법칙이 성립된다는 것이다. 이것이 상대성이라는 것이다.
특수상대성에서 상대성이라는 말은 한시스템이 정지해있고 그 정지한 시스템에서 어떤 다른 시스템이 속도 V로 움직인다고 보고 동일하게 좀전에 움직이던 시스템을 정지해 있다고 보고 내가 반대방향으로 -V 라는 속도로 움직인다고 해도 동일하게 성립된다고 해서 상대성이라는 움직임이 생겼다.
@
bar 가 안붙은 시스템을 표시하면 V 대신에 -V만 넣어주면 된다. 그리고 일부 term 에 bar 를 붙여준다.
$t=\frac{\bar{t}+\frac{V}{C^{2}}\bar{x}}{\sqrt{1-(\frac{V}{C})^{2}}}$
공간에 대해서는 어떻게 되냐면, 동일하게,
$x=\frac{\bar{x}+V\bar{t}}{\sqrt{(1-(\frac{V}{C})^{2})}}$
그리고 움직이는 방향에 수직인 방향은 관계가 없으니까 그대로 변환식이 다음과 같다
$y=\bar{y}, z=\bar{z}$
@
정리하자면,
$\bar{t}=\frac{t-\frac{V}{C^{2}}x}{\sqrt{1-(\frac{V}{C})^{2}}}$
$\bar{x}=\frac{x-Vt}{\sqrt{1-(\frac{V}{C})^{2}}}$
$\bar{y}=y, \bar{z}=z$
$t=\frac{\bar{t}+\frac{V}{C^{2}}\bar{x}}{\sqrt{1-(\frac{V}{C})^{2}}}$
$x=\frac{\bar{x}+V\bar{t}}{\sqrt{(1-(\frac{V}{C})^{2})}}$
$y=\bar{y}, z=\bar{z}$
위 두 수식셋을 가리켜 로렌츠 변환이라고 한다. 아인슈타인 특수상대성이론이 처음 나왔을때 로렌츠 아인슈타인 이론이라고 했다. 로렌츠 변환이 결국은 광속불변의 원칙하에 시공의 변환관계를 이야기 하는 것이다.
@
이렇게 변환된 시스템에서 시간의 팽창과 길이의 수축, 즉, 시공의 변환을 적용해 볼수 있다.
@
먼저 우리가 볼거는 time 에 대한 변환을 알아보겠다. bar가 안붙은 정지한 시스템. V라는 등속도로 움직이는 bar 가 붙은 움직이는 시스템을 생각해보자.
이때, 등속도로 움직이는 시스템이 원점을 $\bar{x} = 0$ 로 둔다. 원점에다 시계를 뒀다 했을때, 이시계는 시간이 $\bar{t_{1}}, \bar{t_{2}}, ...$ 이렇게 쭉 갈거다. 이렇게 가는 시간이 정지한 시스템에서 어떻게 바뀌어 가는가? 다시말해서, $t_{1}, t_{2}, ...$ 이렇게 변환되는 변환관계를 알수 있다는 것이다.
일단, $t_{1}$ 은 어떻게 표시되냐하면, $t_{1} = \frac{\bar{t}+\frac{V}{C^{2}}\bar{x}}{\sqrt{1-(\frac{V}{C})^{2}}}$ 의 수식에서 $\bar{x}=0$ 이다를 이용하면,
$t_{1} = \frac{\bar{t_{1}}}{\sqrt{1-(\frac{V}{C})^{2}}}$ 이고 $t_{2}$ 도 동일하게 이렇게 된다. $t_{2} = \frac{\bar{t_{2}}}{\sqrt{1-(\frac{V}{C})^{2}}}$
$t_{1}, t_{2}$ 는 한순간의 시각이고, 우리가 알고 싶은것은 움직이는 시스템에서의 시계가 정지한 시스템에서 어떻게 보이는가. 움직이는 시스템의 시계의 시간을 정지한 시스템의 시계의 시간으로 환산했을때 어떻게 보이는가.
시간이기 때문에 $t_{2}-t_{1}$ 은 $t_{2}-t_{1}=\frac{\bar{t_{2}}-\bar{t_{1}}}{\sqrt{1-(\frac{V}{C})^{2}}}$
이걸 다시보면 정지한 시스템에서의 시간은 $\Delta t$ 움직이는 시스템 $\sqrt{1-(\frac{V}{C})^{2}}$ 하고 bar가 붙은 시스템 하고 $\Delta\bar{t}$ 이런 관계가 있다는 것이다.
$\Delta t = \frac{\Delta\bar{t}}{\sqrt{1-(\frac{V}{C})^{2}}}$
이 관계에서 우리가 알수있는것은 C의 특성에 의해 $\sqrt{1-(\frac{V}{C})^{2}} \leq 1$ 이다.
그래서 위 수식에서 1보다 작으것으로 나눠주기 때문에 운동하는 시스템의 시간 $\Delta\bar{t}$ 을 정지한 시스템의 시간 $\Delta t$ 으로 바꿔놓고 보면, 움직이는 시스템의 시간이 팽창하는 것이다. 왜냐면 분모가 1보다 작기때문에 전체가 1보다 커지는 것이다. 시간의 팽창이 오는 것이다.
@
두번째로 우리가 봐야할 시스템은 길이를 보자. 움직이는 시스템에서의 길이가 정지한 시스템에서는 어떻게 보이는가
$x_{1}, x_{2}$ 의 가운데 선이 정지한 시스템으로 어떻게 맵핑, 변환되는가. $\bar{x_{1}}$ 는 $x_{1}$ 으로 갈거고 $\bar{x_{2}}$ 는 $x_{2}$ 로 갈것이다. 여기서 중요한 포인트는 정지한 시스템으로 두 포인트를 동시에 보내줘야한다는 것이다. 예를들어, $x_{1}$ 이 먼저 도착하고 한참뒤에 $x_{2}$ 가 오면 안된다.
$\bar{x_{2}}=\frac{x_{2}-Vt_{0}}{\sqrt{1-(\frac{V}{C})^{2}}}$
$\bar{x_{1}}=\frac{x_{1}-Vt_{0}}{\sqrt{1-(\frac{V}{C})^{2}}}$ 이다. 따라서,
$\bar{x_{2}}-\bar{x_{1}}=\frac{x_{2}-x_{1}}{\sqrt{1-(\frac{V}{C})^{2}}}$ 이 된다.
$Vt_{0}$ 가 같으므로,
$\Delta \bar{x}=\frac{\Delta x}{\sqrt{1-(\frac{V}{C})^{2}}}$
따라서, $\Delta x = \sqrt{1-(\frac{V}{C})^{2}} \Delta \bar{x} $
$\sqrt{1-(\frac{V}{C})^{2}}$ 값이 항상 1보다 작으므로, bar 가 안붙은 정지한 시스템에서 $\Delta x$ 움직이는 시스템을 보면 길이가 줄어드는 것이다. 이것이 유명한 로렌츠-피츠제럴드 길이수축이다.
다시말해서, 정지한 시스템에서 움직이는 시스템을 봤을때, 움직이는 시스템의 길이는 움직이는 방향쪽으로 줄어든다.
@
위 두 수식으로부터 정지한 시스템에서 움직이는 시스템을 봤을때, 움직이는 물체의 시간은 팽창하고, 천천히 흘럭가고, 움직이는 시스템의 길이는 나아가는 방향으로 수축을 한다는 것이다.
@
특수상대성이론의 세번째 중요한 포인트는 동시성 이다.
두 시스템에서 한 시스템이 등속도 V로 움직일때, 움직이는 시스템에서 두 이벤트 $A(\bar{t_{1}},\bar{x_{1}}), B(\bar{t_{2}},\bar{x_{2}})$ 가 있었다고 가정하자. 이 두 사건이 정지한 시스템으로 어떻게 매핑, 변환될 것인가.
$t_{1}=\frac{\bar{t_{1}+\frac{V}{C^{2}}\bar{x_{1}}}}{\sqrt{1-(\frac{V}{C})^{2}}}$
$t_{2}=\frac{\bar{t_{2}+\frac{V}{C^{2}}\bar{x_{2}}}}{\sqrt{1-(\frac{V}{C})^{2}}}$
$t_{2}-t_{1}=\frac{(\bar{t_{2}-\bar{t_{1}}})+\frac{V}{C^{2}}(\bar{x_{2}}-\bar{x_{1}})}{\sqrt{1-(\frac{V}{C})^{2}}}$
움직이는 시스템에서 두 사건이 동시에 일어났다고 생각해보자.
@
네번째는 속도의 가산법이다.
움직이는 시스템에서 움직이는게 $\bar{V_{x}}$ 라고 했을 때, 이거를 정지한 시스템에서 봤을때 도대체 이 속도가 어떻게 되는가. 움직이는 시스템의 속도 V가 있고 움직이는 어떤것의 속도 $\bar{V_{x}}$ 가 있는데 말이다.
$\bar{x}\sqrt{1-(\frac{V}{C})^{2}}=x-vt$
$\bar{x}$ 를 고쳐 쓰면
$\bar{V_{x}}\bar{t}\sqrt{1-(\frac{V}{C})^{2}}=x-vt$
$\bar{V_{x}}\bar{t}$ 를, 특히 $\bar{t}$ 를 풀어쓰면
$\bar{V_{x}}\bar{t}\sqrt{1-(\frac{V}{C})^{2}}=\bar{V_{x}}\frac{t-\frac{V}{C^{2}}x}{\sqrt{something}}\sqrt{something}=x-vt$
$\bar{V_{x}}(t-\frac{V}{C^{2}}x)=x-vt$
정리해주면,
$\frac{x}{t}=V_{x}$
$\frac{x}{t}=V_{x}=\frac{\bar{V_{x}}+V}{1+\frac{\bar{V_{x}}V}{C^{2}}}$
$\frac{\bar{V_{x}}+V}{1+\frac{\bar{V_{x}}V}{C^{2}}}$ 이 수식이 속도의 가산법이다.
빛이 반대방향으로 진행하면 광속은 갈릴레이 법칙에 의하면 2C가 되어야한다.
그런데 $\frac{\bar{V_{x}}+V}{1+\frac{\bar{V_{x}}V}{C^{2}}}$ 이 수식에 의하면 절대 광속 C를 넘을 수 없다. 그래서 정확한 속도의 가산법은 이 공식을 써야한다는 것이다.
@
특수상대성이론의 4가지 귀결을 적어보면,
길이는 로렌츠 수축에 의해, 빛이 제랄드 로렌츠 수축이 되서
$l=l_{0}\sqrt{1-(\frac{V}{C})^{2}}$
위 수식은 속도가 광속에 가까워지면 $V \rightarrow C$
l 은 0로 간다. $l \rightarrow 0$
광속으로 움직이는 시스템을 정지하는 시스템이 봤을때 광속으로 달리는 로켓 앞의 공간이 줄어든다는 것이다.
질량은
$m=\frac{m_{0}}{\sqrt{1-(\frac{V}{C})^{2}}}$
시간은
$t=\frac{t_{0}}{\sqrt{1-(\frac{V}{C})^{2}}}$
로켓 속도가 광속이 되면, $V \rightarrow C$
시간은 무한히 천천히 흐른다. $t \rightarrow \infty$
지상에서 달리는 로켓을 봤을때 로켓의 속도가 광속이 되면 지상에서 사람이 봤을때 로켓앞에 전개되는 공간이 줄어들어서 길이가 0가 되고 그때 로켓 안에 있는 시계는 무한히 천천히 간다. 나이를 먹지 않는다. 지상의 정지해 있는 시스템에서 봤을때 그렇다.
빛은 갈길이 없는 곳을 간적이 없고, 나이를 먹지 않았다.
@
특수상대성이론이 가져온 또 하나의 혁명적인 귀결은 에너지와 모멘트이다.
보통 물리관점에서 모멘트는 질량곱하기 속도이다. $P = mv$
이걸 상대론적 관점에서 보면,
$P=\frac{mV}{\sqrt{1-(\frac{V}{C})^{2}}}$
@
또한 에너지도
$E = \frac{mC^{2}}{\sqrt{1-(\frac{V}{C})^{2}}}$
@
이러한 특수상대성이론의 5가지 귀결을 보면 된다. 물리학에서 가장 중요한 모멘텀 P 와 에너지 E 조차도 $\gamma$ factor 를 고려 해 줘야한다.
$\gamma=\frac{1}{\sqrt{1-(\frac{V}{C})^{2}}}$
$\gamma=\frac{1}{\sqrt{1-\beta^{2}}}$
@
다섯가지 공식을 유심히 보면 변수는 하나다. V 하나다. 모두 속도 V에 따라서 바뀐다는 것이다. V 는 등속도이다.
@
$E=\gamma mC^{2}$ 야 말로 $E=mC^{2}$ (정지한 물체의 정지질량에너지를 환산한 것이다.) 보다 더 포괄적인 공식이다.
$E=\gamma mC^{2}$ 공식의 유도는 일과 에너지 관계에서 나온다.
$W=\int_{x_{1}}^{x_{2}} Fdx$
$W=\int_{x_{1}}^{x_{2}} \frac{d\vec{P}}{dt}dx$
위 수식에 $P=\frac{mV}{\sqrt{1-(\frac{V}{C})^{2}}}=\gamma mV$ 를 넣으면,
$W=\frac{mC^{2}}{\sqrt{1-(\frac{V}{C})^{2}}}-mC^{2}$
위의 수식이 운동하는 시스템에 의한 kinetic 에너지가 된다.
$W=\frac{mC^{2}}{\sqrt{1-(\frac{V}{C})^{2}}}-mC^{2}=K$
$\frac{mC^{2}}{\sqrt{1-(\frac{V}{C})^{2}}}=K+mC^{2}$
kinetic 에너지와 정지에너지를 합한 토탈 에너지로 볼수 있다.
따라서 더 포괄적인 공식이다.
@
요약하면, 특수상대성이론은 정지시스템, 등속도 운동 시스템, 두 시스템에 관한 이야기이다. 유일한 변수는 속도 V이다. 내가정지하고 다른게 움직여도 되고, 대상이 정지하고 내가 움직여도 동일한 법칙이 성립한다는 것이다. 이것이 상대성이다. 특수상대성에서 특수는 등속도를 말하는 것이다. 일반상대성의 일반은 가속도운동시스템을 말한다.
@
광속불변법칙과 속도변수 V에 의한 상대성 으로 인해 성립하는게 특수상대성이론이다.
