011. Word2Vec (1)
<![CDATA[
@
Word2Vec has various algorithms such as CBOW, skip-gram, etc
@
We will learn natural language processing
We / will / learn / natural / language / processing
w0 / w1 / w2 / w3 / w4 / w5
@
There is hypothesis
With 8000 words, you can communicate
With 20,000 words, you can read newspaper and book
With 30,000 words, you can know most of practical words
The number of words which average human has is from 8 000 to 20,000
Let's suppose dictionary has 50,000 words
@
One hot encoding
[0 0 0 1 ... 0 0 0] is one hot vector
@
Let's create 50,000 dimension vector
You can arrange words in various ways like frequency, alphabetical order, descending, ascending, etc
In this case, let's arrange words in alphabetical order
We / will / learn / natural / language / processing
language / learn / natural / processing / We / will
language = [1 0 0 0 0 0]
learn = [0 1 0 0 0 0]
natural = [0 0 1 0 0 0]
processing = [0 0 0 1 0 0]
We = [0 0 0 0 1 0]
will = [0 0 0 0 0 1]
@
We input vector into neural net
Neural net outputs vector
@
one dictionary [a, aa, ...] size is $1\times 50,000$
practical full dictionary [0 0 1 ... 0], ...,[0 0 0 ... 0] size to store one word is $50,000\times 50,000$
@
When [0 0 1 0 0] vector goes into neural net, element of vector should be float type to perform arthmetics rather than logical operatioin
This case also increases size of vector
@
It's too wasteful when we have too many 0 in vector
Above way of storing words into vector turned out too inefficient
@
So, we mark index on each word
To do this, we create kind of table
language 0
learn 1
natural 2
processing 3
We 4
will 5
And we store those index numbers
If you have space where those strings(language, learn, ...) are stored, you can store 50,000 words
@
Let's apply this way to given sentence
We / will / learn / natural / language / processing
[4,5,1,2,0,3] means "We will learn natural language processing"
Above step can be expressed by indexing, encoding, or parsing
We use [4,5,1,2,0,3] as dataset
Suppose we have milions of dimension vector [4,5,1,2,0,3,.....] from entire text
We will put batch size(30 or 50 or 100 vectors) data into neural net
In this case, we suppose we use 3 batch size
Then, we process [4,5,1] into one-hot-encoding
Then, one hot encoded vector size will be $3\times 50,000$
We put $3\times 50,000$ dimension vector into neural net
This way is more efficient with saving memory
This way means I create one hot vector in real time
@
How to make one hot vectors
vec = tf.zeros(50000)
i : index
w : word
w0 : 0 index word
vec[wi] = 1
We make [4,5,1] one hot encoding
50,000 dimension vector [0 0 0 1 0 0 ...]
50,000 dimension vector [0 0 0 0 1 0 ...]
50,000 dimension vector [0 1 0 0 0 0 ...]
Now, we made $3\times 50,000$ matrix
@
When you make batch, you get entire index value
You devide entire dataset by index value
First devided vector will be one hot encoded and then be inserted into neural net
@
But we still too huge $3\times 50,000$ matrix
And even it doesn't make good training
because this way is too difficult to express meaning
@
In rule based processing, we analyze grammar, morpheme, etc
Then, we figure out something should be located after other word by probability
We just think some word1 gramartically and probabilistically is followed after word2
But in deep learning, we put meaning into vector
See vector representation of words on tensorflow site
@
I embed words and its meanings, characteristics, etc into vector
Above task is called "word embedding"
A collection of vectors becomes "words"
Embeded one vector is called "embedding"
A collection of vectors is called "embeddings"
@
When you compact some vector, that vector is sparse
Spase vector which is generated from words is not good for machine learning
Word embedding can convert sparse word vector into dense word vector
@
You can think of Word2Vec as preprocessing for nlp
Raw word can be represented in "char"
We can perform indexing on word represented in "char" with resulting one hot vector represented in integer
We can process "one hot vector represented in integer" via Word2Vec, resulting vector represented in dense "float"
We can put "vector represented in dense "float"" into neural net, seq2seq, LSTM, RNN, resulting output
raw word $\overset{indexing}\rightarrow$ one hot vector : simple preprocessing
one hot vector $\overset{Word2Vec}\rightarrow$ vector in dense float : preprocessing using nn
vector in dense float $\overset{nn, rnn, LSTM, seq2seq}\rightarrow$ : nlp model
nlp = preprocessing using nn + nlp model
@
How to perform Word2Vec
You collect every word in the world
Suppose we have 50,000 words
You perform indexing on 50,000 words
You arrange word in order of frequency or alphabet, etc with marking index number on each word
For example, suppose this sentence
We will learn natural language processing
suppose following index information
We 1028
will 356
learn 3
natural 2680
language 170
processing 394
one hot vector for "We" = [0 0 .. 1 ... 0] = vector[1028] is 1
$50000\times 200$ WeightMatrix $\cdot$ $1\times 50000$ VectorForWe = $200\times 1$Vector
We can arbitrary choose from 200 to 300 for row size
I transpose $50000\times 200$ $WeightMatrix^{T}$
$200\times 1$Vector $\cdot$ $200\times 50000$ WeightMatrix = $50000\times 1$ Vector
$50000\times 1$ Vector should be "will"
one hot vector for "will" = [0 ... 1 0 0 ... 0] = vector[356] is 1
We consider "$50000\times 1$ Vector" as output
We consider "[0 ... 1 0 0 ... 0]" as label
Then, we calculate nce(noise contrastive estimation) loss
We put output and label into nce loss function and get loss
Then, we perform gradient descent and back propagation and update WeightMatrix
img 218a759d-9560-41c5-827b-a6bda38c4b0d
]]>
<![CDATA[
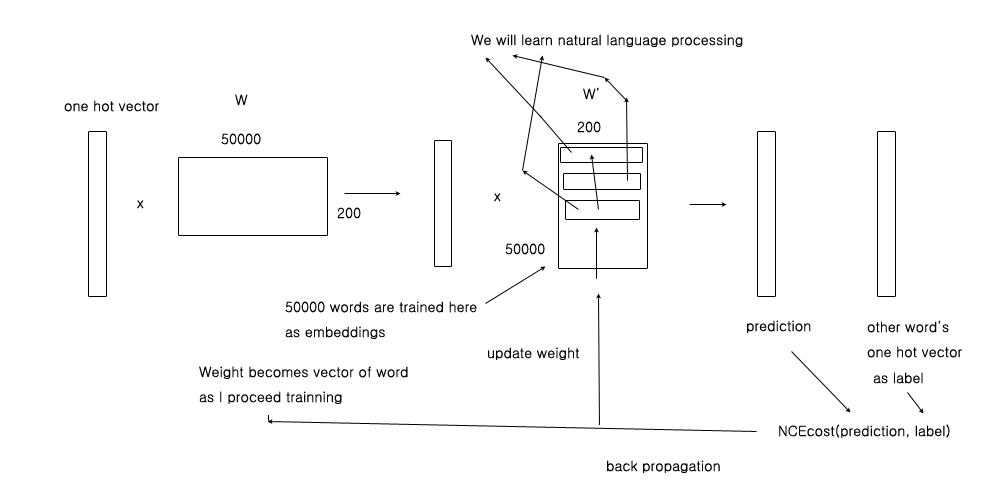If summary, "We" is converted into one hot vector
1*50000 one hot vector of "We" x 50000*200 weight = 1*200 vector
1*200 vector x 200*50000 weight' = 1*50000 prediction vector for "will"
We make one hot vector for "will" to use it as label
We calculate loss with 1*50000 prediction vector for "will" and 1*50000 label vector of "will"
We perform "gradient descent" and "back propagation" to update weight'
First vector of weight' represents "We"
Second vector of weight' represents "will"
Those multiple vectors are "embeddings"
@
word sparse one hot vector x 50000*200 W -> dense float vector x 200*50000 W' -> prediction one hot vector --- label one hot vector
In word one hot vector x W, let's think if multiplication has meaning because too many 0 are multiplied
Result will be 1*200 vector
img 7ad276d9-28ba-49c6-a315-4bfe6fa2cbde
Multiplication is nothing but bringing entire row and index is word's index
W[r][wordindex]
This method extracts one entire column so we don't need to perform above multiplication
params : weight
ids : set of index represented in list
tf.nn.embedding_lookup(params, ids, partition_strategy='mod', name=None, validate_indices=True, max_norm=None)
By using tf.nn.embedding_lookup(), model becomes simple
200*1 dense vector x 50000*200 Weight -> 50000*1 output vector --- label
if word index is 137, we do like this
tf.nn.embedding_lookup(Weight, [137]) returns 200*1 dense vector
Above step with "tf.nn.embedding_lookup(Weight, [137]) returns 200*1 dense vector" is called "projection"
@
How to train?
We use CBOW which is not much used because of low performance or skip-gram
CBOW is to fill blank
We will learn
We w( )ll learn
training set becomes [W e w l]
[W e w l] x Weight = output vector --- label vector
output vector should be vector for "i"
label vector is vector for "i"
@
skip-gram is to answer around words if I know some words
W( ) le( )rn l( )ng( )age
I should infer ( ) by seeing 'e' or 'r'
Following is CBOW's dataset
W( ) le( )rn l( )ng( )age
Train dataset feature $\begin{bmatrix} [W, l, e, r] \\ [l, e, r, n] \\ [e, r, n, l] \\ [r, n, l, n] \\ [n, l, n, g] \\ ... \end{bmatrix}$
Train dataset label $\begin{bmatrix} e \\ a \\ a \\ a \\ a \end{bmatrix}$
Following is skip-gram's dataset
W( ) le( )rn l( )ng( )age
$\begin{bmatrix} [e] \\ [e] \\ [e] \\ [e] \\ [e] \\ [e] \\ ... \end{bmatrix} \begin{bmatrix} [w] \\ [l] \\ [e] \\ [a] \\ [r] \\ [n] \\ ... \end{bmatrix}$
Train dataset feature --- Train dataset label
[e] [w] is one set which is small size
]]>