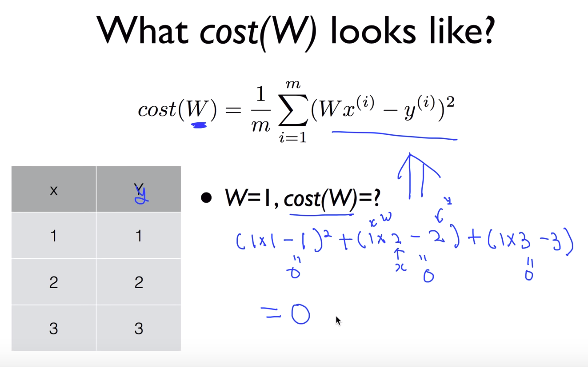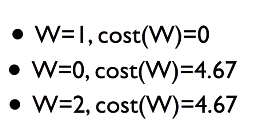================================================== You can make hypothesis function (or function which represents your neural network) as follow $$$H(x)=Wx+b$$$ Once you have your hypothesis function you can also make cost function which represents how much of difference your neural network has between your prediction and ground truth $$$cost(W,b)= \dfrac{1}{m} \sum\limits_{i=1}^m (H(x^{(i)})-y^{(i)})^2$$$ Goal of linear regression (or goal of training neural network) is to find W and b which minimize cost value by using your data and backpropagation ================================================== For simplicity, suppose your model is as following without bias b term $$$H(x)=Wx$$$ Then cost function can be written as follwo $$$cost(W)= \dfrac{1}{m} \sum\limits_{i=1}^m (H(x^{(i)})-y^{(i)})^2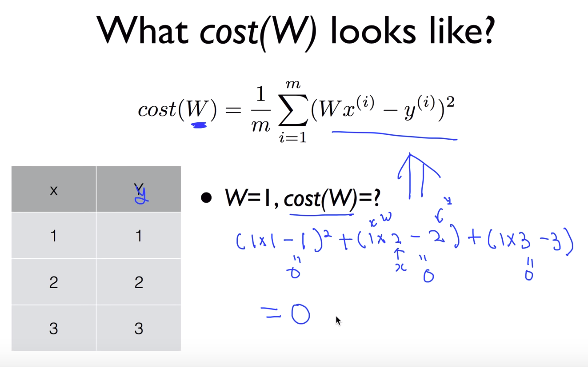$$$ ================================================== When w=1, and when you know x values as data you can calculate cost values ================================================== ================================================== 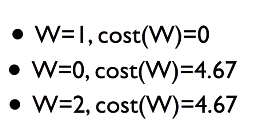You can draw graph based on relationship between W and cost ================================================== Goal is to find specific W value which makes cost minimum You can find above point W if you can draw graph of cost function by using optimization methods like gradient descent algorithm ================================================== You can move down along with slope of loss function When slope is 0, that can mean that you don't have place to move down $$$\text{updated } W \leftarrow W -\alpha \dfrac{\partial cost(W)}{\partial{W}}$$$ Let's use learning rate $$$\alpha = 0.1$$$ You find slope of cost(W) with respect to W by using partial derivative Let's say $$$\dfrac{\partial cost(W)}{\partial{W}}=10$$$ $$$0.1 \times 10 = 1$$$ Then, you can find 'new updated W which is supposed to be moved to left' according to above formular $$$\text{updated } W \leftarrow W -\alpha \dfrac{\partial cost(W)}{\partial{W}}$$$ specically $$$\text{new updated } W = \text{current } W - 1$$$ which means you most W towards left as much as 1 If $$$\dfrac{\partial cost(W)}{\partial{W}}$$$ is less than 0 (in other words negative slope) W will move towards right for example $$$\text{updated } W \leftarrow W - (-1)$$$ ================================================== To prevent minimization from falling into local minima, you'd better confirm whether your loss function $$$L(W, b)$$$ forms convex shape in advance ================================================== You can use gradient descent algorithm to find optimal W but likelyhood you can fall into local minima is high per starting points 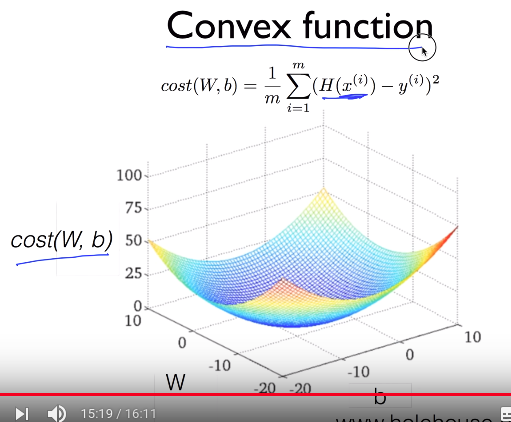================================================== This shape is good