006-lec-002. softmax function for logistic regression(multinomial classification)
@
softmax function
$$$S(y_{i})=\frac{e^{y_{i}}}{\sum\limits_{j}e^{y_{j}}}$$$
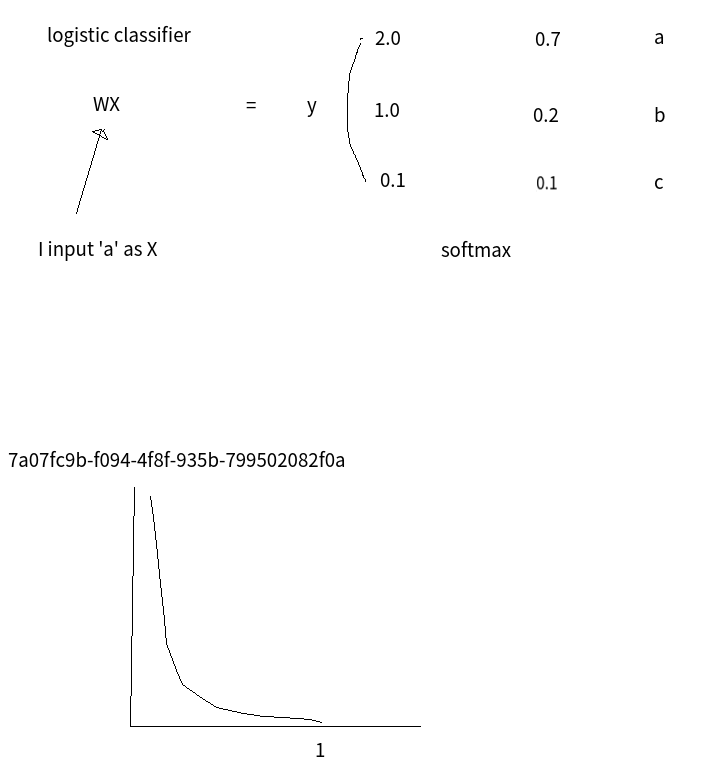
output layer y has scores: 2.0, 1.0, 0.1
You can pass scores into softmax function
Then, you obtain probabilities: 0.7,0.2,0.1
probability of occurring a is 0.7
probability of occurring b is 0.2
probability of occurring c is 0.1
Then, you can perform one hot encoding,
with converting highest value(0.7) into 1.0 and remainders(0.2, 0.1) into 0.0
You can use argmax() of tensorflow to do this
@
You use cross entropy function as loss function for multinomial classification(logistic regression)
Let's say you have $$$\hat{Y}$$$ and Y
You can find difference between them by using cross entropy function
$$$Label_{i}$$$ : ith label
$$$\sum\limits_{i} [(Label_{i}) \bigodot (-\log{\hat{y}_{i}})]$$$
Let's suppose one example
0: A
1: B
$$$Label=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$$$
$$$\hat{Y}=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$$$
This is right prediction
Let's find loss $$$\sum\limits_{i} [(Label_{i}) \bigodot (-\log{\hat{y}_{i}})]$$$
$$$\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot -\log{\begin{bmatrix} 0 \\ 1 \end{bmatrix}}$$$
# img 7a07fc9b-f094-4f8f-935b-799502082f0a
 $$$\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot \begin{bmatrix} \infty \\ 0 \end{bmatrix}$$$
$$$\begin{bmatrix} 0 \\ 0 \end{bmatrix}$$$
You sum all elements up,
then, you will get 0,
this is loss value when prediction is right
Let's see other case
$$$\hat{Y}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$
$$$\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot -\log{\begin{bmatrix} 1 \\ 0 \end{bmatrix}}$$$
$$$=\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot \begin{bmatrix} 0 \\ \infty \end{bmatrix}$$$
$$$=\begin{bmatrix} 0 \\ \infty \end{bmatrix}$$$
You sum all elements up,
you will get $$$\infty$$$,
this is loss value when prediction is wrong
What you saw in previous lecture,
$$$CrossEntropyFunction(H(x),y)=y\log{(H(x))}-(1-y)\log{(1-H(x))}$$$,
is actually cross entropy function,
as loss function for hypothesis function of logistic regression
$$$CrossEntropyFunction(H(x),y)=y\log{(H(x))} - (1-y)\log{(1-H(x))}$$$
$$$D(S,L)=\sum\limits_{i} [(L_{i}) \bigodot (-\log{S_{i}})]$$$
$$$S=H(x)=\hat{y}$$$
L=y
$$$\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot \begin{bmatrix} \infty \\ 0 \end{bmatrix}$$$
$$$\begin{bmatrix} 0 \\ 0 \end{bmatrix}$$$
You sum all elements up,
then, you will get 0,
this is loss value when prediction is right
Let's see other case
$$$\hat{Y}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$
$$$\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot -\log{\begin{bmatrix} 1 \\ 0 \end{bmatrix}}$$$
$$$=\begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigodot \begin{bmatrix} 0 \\ \infty \end{bmatrix}$$$
$$$=\begin{bmatrix} 0 \\ \infty \end{bmatrix}$$$
You sum all elements up,
you will get $$$\infty$$$,
this is loss value when prediction is wrong
What you saw in previous lecture,
$$$CrossEntropyFunction(H(x),y)=y\log{(H(x))}-(1-y)\log{(1-H(x))}$$$,
is actually cross entropy function,
as loss function for hypothesis function of logistic regression
$$$CrossEntropyFunction(H(x),y)=y\log{(H(x))} - (1-y)\log{(1-H(x))}$$$
$$$D(S,L)=\sum\limits_{i} [(L_{i}) \bigodot (-\log{S_{i}})]$$$
$$$S=H(x)=\hat{y}$$$
L=y
