==================================================
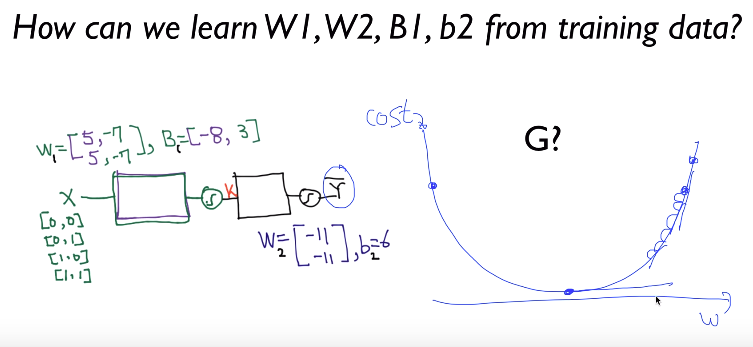 Let's see idea about how to train neural network
Goal of training neural network is to minimize "cost"
See graph, "cost" is written in vertical axis
weight w is written in horizontal axis
Another expression of goal is to make differentiation (slope) w
with respect to cost minimize
See graph, slope at top right point is high
But slope decreases as training goes
Finally, if training converges, you can reach to lowest point
which has almost 0 slope
==================================================
Let's see idea about how to train neural network
Goal of training neural network is to minimize "cost"
See graph, "cost" is written in vertical axis
weight w is written in horizontal axis
Another expression of goal is to make differentiation (slope) w
with respect to cost minimize
See graph, slope at top right point is high
But slope decreases as training goes
Finally, if training converges, you can reach to lowest point
which has almost 0 slope
==================================================
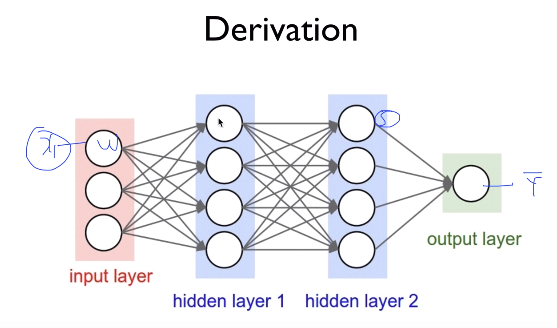 Conceptually, you should know "amont of effect to $$$\hat{y}$$$ by $$$x_1$$$
to adjust $$$w_1$$$
==================================================
Conceptually, you should know "amont of effect to $$$\hat{y}$$$ by $$$x_1$$$
to adjust $$$w_1$$$
==================================================
 Aside from effect to $$$\hat{y}$$$ by $$$x_1$$$
you also should know effects to $$$\hat{y}$$$ by all other x like $$$x_2$$$, $$$x_3$$$, ...
But this is very high computationally burden
==================================================
Aside from effect to $$$\hat{y}$$$ by $$$x_1$$$
you also should know effects to $$$\hat{y}$$$ by all other x like $$$x_2$$$, $$$x_3$$$, ...
But this is very high computationally burden
==================================================
 So professor M. Minsky concluded this kind of computation couldn't be possible
because it'd be too high computationally burden
==================================================
Above issue had been resolved by backpropagation algorithm
So professor M. Minsky concluded this kind of computation couldn't be possible
because it'd be too high computationally burden
==================================================
Above issue had been resolved by backpropagation algorithm
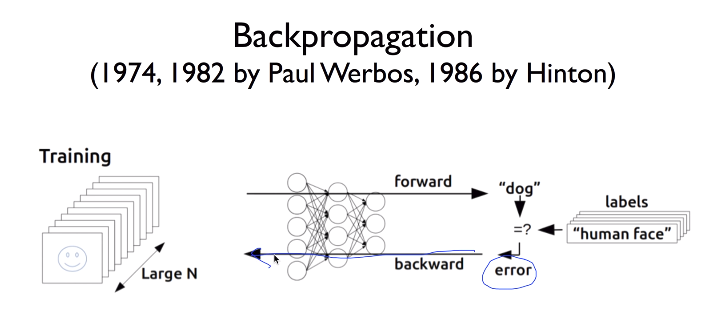 Idea of backpropagation is
1. you calculate error (loss or cost)
2. you pass error from last layer to first layers, that is backward direction
3. through "2." step, you can calculate "derivative values"
and you can decide how and what to update
==================================================
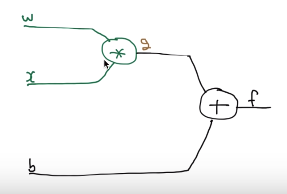
$$$f=wx+b$$$
You can replace $$$wx$$$ with $$$g$$$
then, you can write
$$$g=wx$$$
Then, you can write $$$f=wx+b$$$ as follow
$$$f=g+b$$$
==================================================
You can draw graph about above equations
Idea of backpropagation is
1. you calculate error (loss or cost)
2. you pass error from last layer to first layers, that is backward direction
3. through "2." step, you can calculate "derivative values"
and you can decide how and what to update
==================================================
$$$f=wx+b$$$
You can replace $$$wx$$$ with $$$g$$$
then, you can write
$$$g=wx$$$
Then, you can write $$$f=wx+b$$$ as follow
$$$f=g+b$$$
==================================================
You can draw graph about above equations
 ==================================================
==================================================
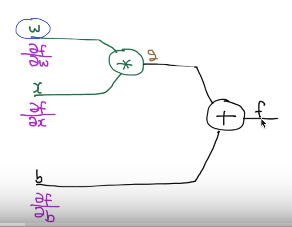 $$$\dfrac{\partial f}{\partial w}$$$: effect to f by w
$$$\dfrac{\partial f}{\partial x}$$$: effect to f by x
$$$\dfrac{\partial f}{\partial b}$$$: effect to f by b
==================================================
One technique you need to know to use backpropagation is chainrule
$$$y=f(g(x))$$$
$$$\dfrac{\partial y}{\partial x} =
\dfrac{\partial y}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
==================================================
$$$\dfrac{\partial f}{\partial w}$$$: effect to f by w
$$$\dfrac{\partial f}{\partial x}$$$: effect to f by x
$$$\dfrac{\partial f}{\partial b}$$$: effect to f by b
==================================================
One technique you need to know to use backpropagation is chainrule
$$$y=f(g(x))$$$
$$$\dfrac{\partial y}{\partial x} =
\dfrac{\partial y}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
==================================================
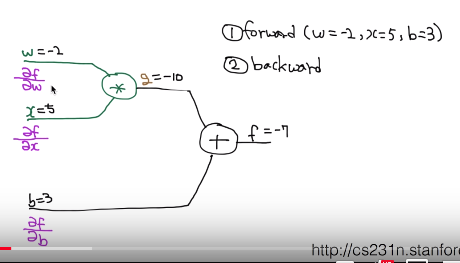 Step 1. Forward phase
Just suppose you have weight w, input x, bias b
as -2, 5, 3
Then, you can get values of $$$g$$$ and $$$f$$$ as $$$-10$$$ and $$$-7$$$
==================================================
You perform several derivatives in advance for backpropagation
From $$$g=wx$$$, you can make
$$$\dfrac{\partial g}{\partial w}=x$$$
$$$\dfrac{\partial g}{\partial x}=w$$$
From $$$f=g+b$$$, you can make
$$$\dfrac{\partial f}{\partial g}=1$$$
$$$\dfrac{\partial f}{\partial b}=1$$$
==================================================
Step 1. Forward phase
Just suppose you have weight w, input x, bias b
as -2, 5, 3
Then, you can get values of $$$g$$$ and $$$f$$$ as $$$-10$$$ and $$$-7$$$
==================================================
You perform several derivatives in advance for backpropagation
From $$$g=wx$$$, you can make
$$$\dfrac{\partial g}{\partial w}=x$$$
$$$\dfrac{\partial g}{\partial x}=w$$$
From $$$f=g+b$$$, you can make
$$$\dfrac{\partial f}{\partial g}=1$$$
$$$\dfrac{\partial f}{\partial b}=1$$$
==================================================
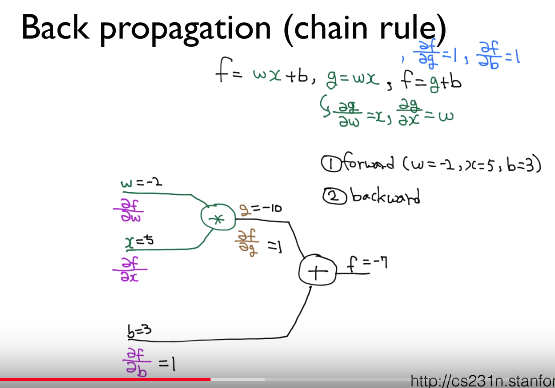 In above screenshot,
you can see $$$\dfrac{\partial f}{\partial g}$$$ and $$$\dfrac{\partial f}{\partial b}$$$
are calcuated as 1 and 1
==================================================
You're going to calculate $$$\dfrac{\partial f}{\partial w}$$$
by using chain rule
$$$\dfrac{\partial f}{\partial w} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial w}$$$
$$$= 1 \times 5$$$
$$$= 5$$$
==================================================
$$$\dfrac{\partial f}{\partial x} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
$$$= 1 \times -2$$$
$$$= -2$$$
==================================================
In above screenshot,
you can see $$$\dfrac{\partial f}{\partial g}$$$ and $$$\dfrac{\partial f}{\partial b}$$$
are calcuated as 1 and 1
==================================================
You're going to calculate $$$\dfrac{\partial f}{\partial w}$$$
by using chain rule
$$$\dfrac{\partial f}{\partial w} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial w}$$$
$$$= 1 \times 5$$$
$$$= 5$$$
==================================================
$$$\dfrac{\partial f}{\partial x} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
$$$= 1 \times -2$$$
$$$= -2$$$
==================================================
 Now, you calculated all effects to f by $$$w, x, b$$$
==================================================
Meaning
$$$\dfrac{\partial f}{\partial w}$$$: effect to f by w is 5 amount intensity
So, if you make w -1 from -2,
that means you performed +1 on -2
Since $$$1 \times 5 = 5$$$,
you should +5 on f according to $$$\dfrac{\partial f}{\partial w}=5$$$
Let's perform operation manually to check whether above calculate is correct
$$$w=-1, x=5 \rightarrow -1 \times 5 = -5$$$
$$$-5 + 3=-2$$$
Since $$$-7 + 5 = -2$$$, above calculate is correct
==================================================
Now, you calculated all effects to f by $$$w, x, b$$$
==================================================
Meaning
$$$\dfrac{\partial f}{\partial w}$$$: effect to f by w is 5 amount intensity
So, if you make w -1 from -2,
that means you performed +1 on -2
Since $$$1 \times 5 = 5$$$,
you should +5 on f according to $$$\dfrac{\partial f}{\partial w}=5$$$
Let's perform operation manually to check whether above calculate is correct
$$$w=-1, x=5 \rightarrow -1 \times 5 = -5$$$
$$$-5 + 3=-2$$$
Since $$$-7 + 5 = -2$$$, above calculate is correct
==================================================
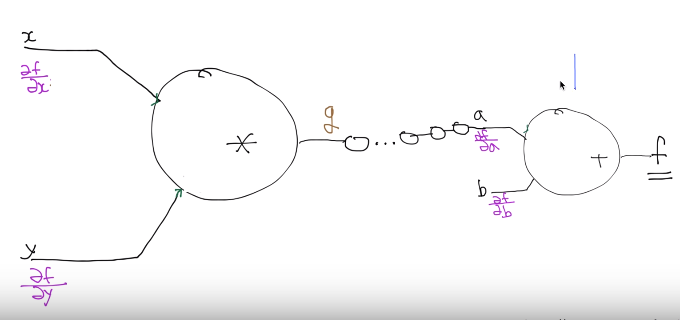 Case where there are more nodes (like more layers)
Logic is same
==================================================
Case where there are more nodes (like more layers)
Logic is same
==================================================
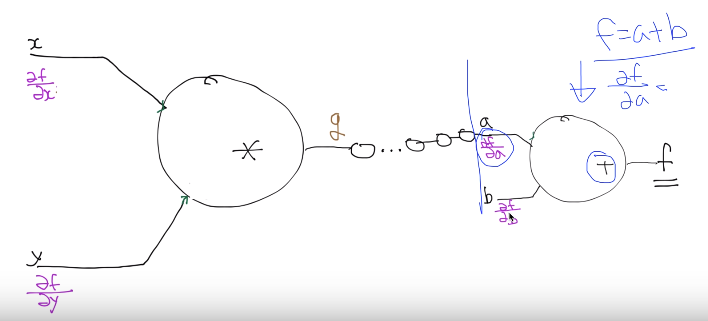 You start with last node (next to f)
Operation of that node is +
Since you know operation on that node
and you know function f as f=a+b
you can calculate $$$\dfrac{\partial f}{\partial a}$$$
==================================================
Suppose you've calculated $$$\dfrac{\partial f}{\partial g}$$$
Then, what you actually want to calculate is
$$$\dfrac{\partial f}{\partial x}$$$
In that situation, you already know $$$\dfrac{\partial g}{\partial x}$$$
because you know operation ($$$*$$$) on that node
Since that operation is $$$*$$$
you can write $$$x*y=g$$$
Then, you can calculate $$$\dfrac{\partial g}{\partial x}$$$ using $$$x*y=g$$$
==================================================
You can calculate $$$\dfrac{\partial f}{\partial x}$$$ using chain rule
$$$\dfrac{\partial f}{\partial x} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
Then, you can finally calculate effect to f by x
which will be used for updating neural network with minimizing loss value
You start with last node (next to f)
Operation of that node is +
Since you know operation on that node
and you know function f as f=a+b
you can calculate $$$\dfrac{\partial f}{\partial a}$$$
==================================================
Suppose you've calculated $$$\dfrac{\partial f}{\partial g}$$$
Then, what you actually want to calculate is
$$$\dfrac{\partial f}{\partial x}$$$
In that situation, you already know $$$\dfrac{\partial g}{\partial x}$$$
because you know operation ($$$*$$$) on that node
Since that operation is $$$*$$$
you can write $$$x*y=g$$$
Then, you can calculate $$$\dfrac{\partial g}{\partial x}$$$ using $$$x*y=g$$$
==================================================
You can calculate $$$\dfrac{\partial f}{\partial x}$$$ using chain rule
$$$\dfrac{\partial f}{\partial x} =
\dfrac{\partial f}{\partial g} \times
\dfrac{\partial g}{\partial x}$$$
Then, you can finally calculate effect to f by x
which will be used for updating neural network with minimizing loss value











