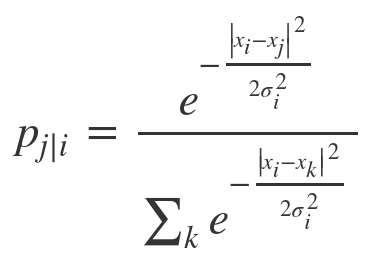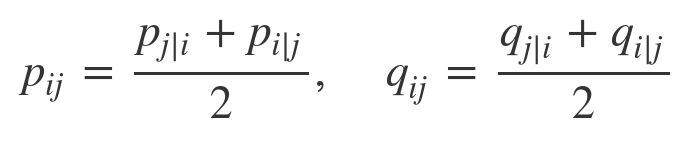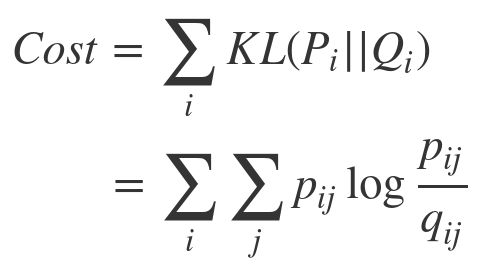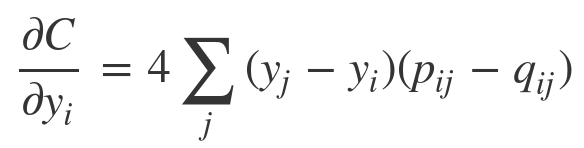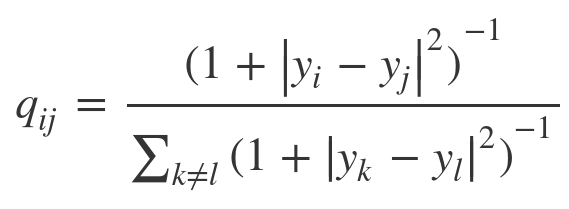https://ratsgo.github.io/machine%20learning/2017/04/28/tSNE/
================================================================================
t-SNE are for "dimensionality reduction" and "visualization"
================================================================================
t-SNE visualizes "high dimensional data like word vector"
================================================================================
y=tSNE(x)
x: data in high dimension
y: data in low dimension
tSNE: trainable
$$$|x-x_{\text{neighbors}}|$$$: should be preserved as much as possible
Distance $$$|x-x_{\text{neighbors}}|$$$ is represented stochastically
================================================================================
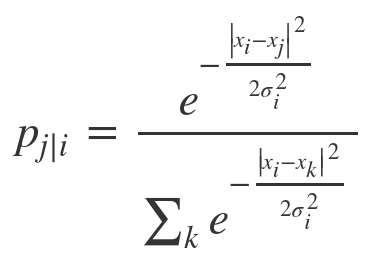 $$$p_{j|i}$$$: when $$$x_i$$$ is given, probability of $$$x_j$$$ occurring
$$$x_j$$$: jth neighbor of $$$x_i$$$
================================================================================
$$$p_{j|i}$$$: when $$$x_i$$$ is given, probability of $$$x_j$$$ occurring
$$$x_j$$$: jth neighbor of $$$x_i$$$
================================================================================
 $$$q_{j|i}$$$: when $$$y_i$$$ is given, probability of $$$y_j$$$ occurring
$$$y_j$$$: jth neighbor of $$$y_i$$$
================================================================================
Goal of SNE: reduce the difference between p and q
================================================================================
probability_distribution_1
probability_distribution_2
if probability_distribution_1==probability_distribution_2:
kullback_leibler_divergence->0
elif probability_distribution_1!=probability_distribution_2:
kullback_leibler_divergence->1
================================================================================
So, you can use kullback_leibler_divergence as cost function for SNE
$$$q_{j|i}$$$: when $$$y_i$$$ is given, probability of $$$y_j$$$ occurring
$$$y_j$$$: jth neighbor of $$$y_i$$$
================================================================================
Goal of SNE: reduce the difference between p and q
================================================================================
probability_distribution_1
probability_distribution_2
if probability_distribution_1==probability_distribution_2:
kullback_leibler_divergence->0
elif probability_distribution_1!=probability_distribution_2:
kullback_leibler_divergence->1
================================================================================
So, you can use kullback_leibler_divergence as cost function for SNE
 ================================================================================
Tricks to increase the training speed on SNE
- Omit $$$\sigma_i$$$ and use constant
- $$$\sigma_i$$$: prevents "probability" from being tortured
because each vector has different probability of chosen
- Solve equation with supposing that following 2 probabilities are same
"when i-data is given, probability of j-data occurring"
"when j-data is given, probability of i-data occurring"
================================================================================
By using above 2 tricks, you can newly write p and q
================================================================================
Tricks to increase the training speed on SNE
- Omit $$$\sigma_i$$$ and use constant
- $$$\sigma_i$$$: prevents "probability" from being tortured
because each vector has different probability of chosen
- Solve equation with supposing that following 2 probabilities are same
"when i-data is given, probability of j-data occurring"
"when j-data is given, probability of i-data occurring"
================================================================================
By using above 2 tricks, you can newly write p and q
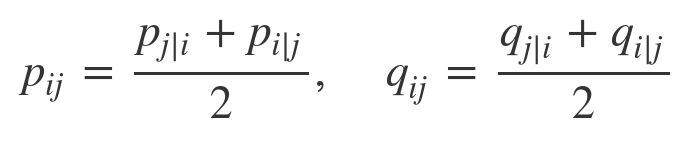 ================================================================================
Therefore, you can write cost function by using new p and q
================================================================================
Therefore, you can write cost function by using new p and q
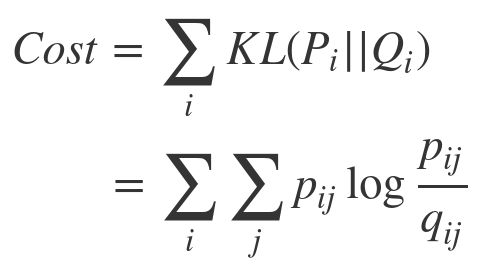 ================================================================================
Calculate partial derivatives (gradient) of cost $$$C$$$ wrt neighbor-data $$$y_i$$$
================================================================================
Calculate partial derivatives (gradient) of cost $$$C$$$ wrt neighbor-data $$$y_i$$$
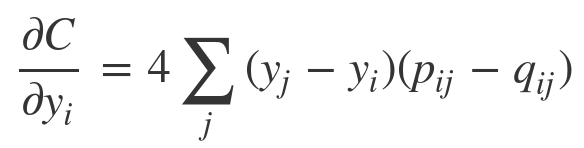 ================================================================================
Note that your goal is to find "y" in low dimension
SNE updates SNE by using gradient descent
- Initialize y
- Update y by using direction and size of gradient
================================================================================
SNE supposes you are dealing with "Gaussian Normal distribution"
Crowding problem is caused by "Gaussian Normal distribution"
because "Gaussian Normal distribution" has not-thick tails
Crowding problem:
prob1=when i-data is given, probability of j-data-far occurring
prob2=when i-data is given, probability of j-data-near occurring
prob1 $$$\sim$$$ prob2
================================================================================
How to solve "crowding problem"?
Use "Gaussian Normal distribution" which has thick tails
This is t-SNE
================================================================================
t-SNE
$$$p_{i|j}$$$: same
$$$q_{i|j}$$$: use t-distribution to make tails thick
================================================================================
Note that your goal is to find "y" in low dimension
SNE updates SNE by using gradient descent
- Initialize y
- Update y by using direction and size of gradient
================================================================================
SNE supposes you are dealing with "Gaussian Normal distribution"
Crowding problem is caused by "Gaussian Normal distribution"
because "Gaussian Normal distribution" has not-thick tails
Crowding problem:
prob1=when i-data is given, probability of j-data-far occurring
prob2=when i-data is given, probability of j-data-near occurring
prob1 $$$\sim$$$ prob2
================================================================================
How to solve "crowding problem"?
Use "Gaussian Normal distribution" which has thick tails
This is t-SNE
================================================================================
t-SNE
$$$p_{i|j}$$$: same
$$$q_{i|j}$$$: use t-distribution to make tails thick
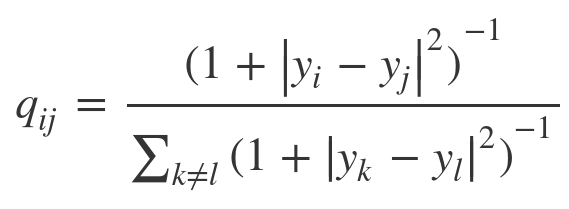 ================================================================================
Usecase of t-SNE
1.
embedding_vector=word2vec(token_sentence)
visualize: tSNE(embedding_vector)
2.
clustered_docs=clustering(many_documents)
visualize: tSNE(clustered_docs)
================================================================================
================================================================================
Usecase of t-SNE
1.
embedding_vector=word2vec(token_sentence)
visualize: tSNE(embedding_vector)
2.
clustered_docs=clustering(many_documents)
visualize: tSNE(clustered_docs)
================================================================================