https://ratsgo.github.io/statistics/2017/05/31/gibbs/
/mnt/1T-5e7/mycodehtml/Data_mining/Gibss_sampling/Ratsgo/main.html
================================================================================
Gibbs sampling
- Probabilistic algorithm
- Generates samples based on joint probability distribution of over-2 random variables
- Much used to approximate "joint probability distribution"
- Much used to approximate calculating probability of "joint probability distribution"
- Gibbs sampling $$$\subset$$$ Markov Chain Monte Carlo
================================================================================
Monte Carlo method
- Select random sample
- Calculate output value of function by using sample in the probabilistic way
- When output value of function can't be expressed in the closed form
- When output value of function is too complicated
- MC is used to approximate "output value of fucntion"
================================================================================
Calculate circle rate by using MC
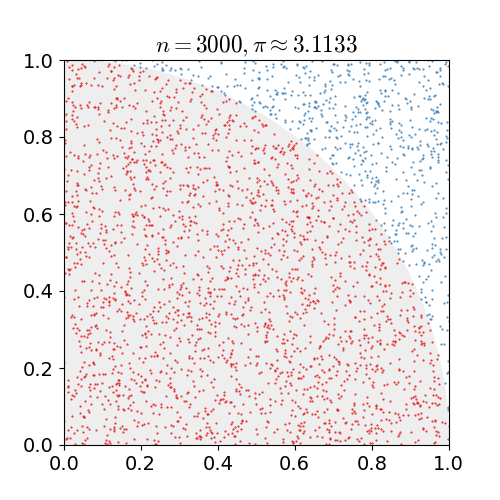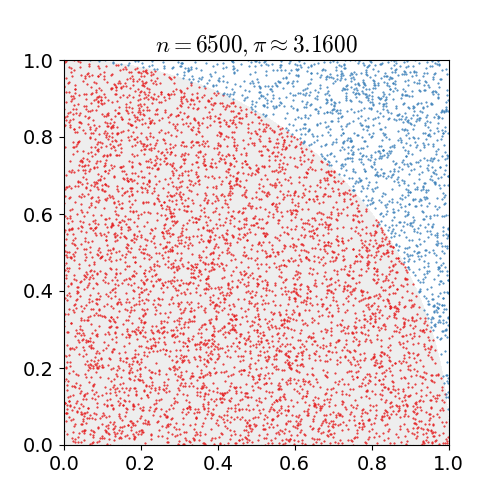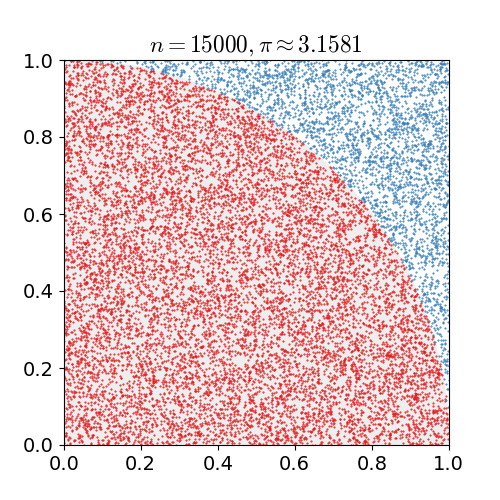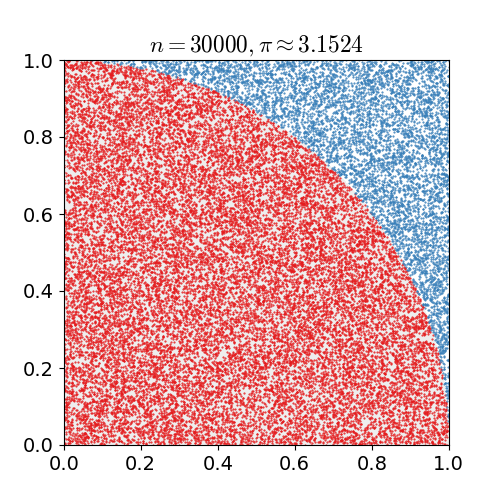 - From the space [0,1] $$$\times$$$ [0,1],
randomly choose the point $$$(x,y)$$$
- Above point is included the circle (whose radius is 1)?
Calculate following inequality equation, $$$x^2+y^2 \le 1$$$
True: point is classified into red point
False: point is classified into blue point
- Iterate above 2 steps
- Caculate following
$$$\dfrac{\text{number of red point}}{\text{number of entire point}}$$$
- Above output becomes nearly $$$\frac{\pi}{4}$$$
- You can finally approximate $$$\pi$$$ by using $$$\frac{\pi}{4}$$$
================================================================================
Markov Chain
- Discrete time based probabilistic process which follows Markov assumption
- Markov assumption
- state probability at time t depends on "the very previous state"
- Transition (from previous one to current one) doesn't require the long history of state transition
- Transition can be inferenced by using "the very previous state"
- Markov assumption in math form
/home/young/Pictures/2019_06_02_08:36:20.png
- With "specific condition being satisfied",
if you interate "Markov Chain",
"probability of current state" becomes equal to "probability of the very previous state"
- Probability distribution which arrvies to equilibrium state is called "stationary distribution"
================================================================================
Markov Chain Monte Carlo
- Monte Carlo method which makes sample
from the probability distribution which follows Markov Chain
How to do
- Create "Markov Chain" which has target distribution
(where you want to make sample from)
- Target distribution should be equal to "stationary distribution" of "Markov Chain"
- Run the simulation of this "Markov Chain"
- After passing "burn-in period" (where values are affected by "random initial values")
you can generate samples which follow "above defined target distribution
as well as stationary distribution of the Markov Chain"
================================================================================
Gibbs sampling
- Gibbs sampling $$$\subset$$$ MCMC
- MC
- all samples are independent
- probability of sample chosen is random
- MCMC
- It is based on "Markov Chain"
- Next sample is affected by current sample
- Gibbs sampling
- It is based on "Markov Chain"
- Next sample is affected by current sample
- Preserves all variables but it affects "only one variable"
================================================================================
Example of Gibbs sampling
- Joint probability distribution of 3 random variables
$$$p(x_1,x_2,x_3)$$$
- You want to create "one sample" from that joint probability distribution
================================================================================
Let's do above sampling by using Gibbs sampling
- Make one ramdom sample, $$$X^0 = (x_1^0,x_2^0,x_3^0)$$$
- Change only one random variable (like $$$X_1$$$)
and make next new sample $$$X^1$$$
- When you use sample, you throw away $$$X^0$$$ and you will use only $$$X^1$$$
================================================================================
Let's see more detail about following step
/ Change only one random variable (like $$$X_1$$$) /
/ and make next new sample $$$X^1$$$ /
- Fix 2 random variables' value $$$x_2^0,x_3^0$$$ from give sample $$$X^{0}$$$
- Create new $$$x_1^1$$$ based on following probability, $$$p(x_1^1|x_2^0,x_3^0)$$$
- Fix 2 random variables' value $$$x_1^1,x_3^0$$$ from give sample $$$X^{0}$$$
- Create new $$$x_2^1$$$ based on following probability, $$$p(x_2^1|x_1^1,x_3^0)$$$
- Fix 2 random variables' value $$$x_1^1,x_2^1$$$ from give sample $$$X^{0}$$$
- Create new $$$x_3^1$$$ based on following probability, $$$p(x_3^1|x_1^1,x_2^1)$$$
- You get final $$$X^1$$$ as $$$X^1 = (x_1^1,x_2^1,x_3^1)$$$
================================================================================
Conditional probability like $$$p(x_1^1|x_2^0,x_3^0)$$$ is proportinal
to joint probability distribution $$$p(x_1,x_2,x_3)$$$
In the initial periods, samples are strongly dependent on initial status $$$X^0$$$
But after you make many sample, initial status becomes no effect
It means you can make sample based on joint probability distribution p
================================================================================
Suppose you want to make samples which follows 2D Gaussian Normal distribution
by using Gibbs sampling
- From the space [0,1] $$$\times$$$ [0,1],
randomly choose the point $$$(x,y)$$$
- Above point is included the circle (whose radius is 1)?
Calculate following inequality equation, $$$x^2+y^2 \le 1$$$
True: point is classified into red point
False: point is classified into blue point
- Iterate above 2 steps
- Caculate following
$$$\dfrac{\text{number of red point}}{\text{number of entire point}}$$$
- Above output becomes nearly $$$\frac{\pi}{4}$$$
- You can finally approximate $$$\pi$$$ by using $$$\frac{\pi}{4}$$$
================================================================================
Markov Chain
- Discrete time based probabilistic process which follows Markov assumption
- Markov assumption
- state probability at time t depends on "the very previous state"
- Transition (from previous one to current one) doesn't require the long history of state transition
- Transition can be inferenced by using "the very previous state"
- Markov assumption in math form
/home/young/Pictures/2019_06_02_08:36:20.png
- With "specific condition being satisfied",
if you interate "Markov Chain",
"probability of current state" becomes equal to "probability of the very previous state"
- Probability distribution which arrvies to equilibrium state is called "stationary distribution"
================================================================================
Markov Chain Monte Carlo
- Monte Carlo method which makes sample
from the probability distribution which follows Markov Chain
How to do
- Create "Markov Chain" which has target distribution
(where you want to make sample from)
- Target distribution should be equal to "stationary distribution" of "Markov Chain"
- Run the simulation of this "Markov Chain"
- After passing "burn-in period" (where values are affected by "random initial values")
you can generate samples which follow "above defined target distribution
as well as stationary distribution of the Markov Chain"
================================================================================
Gibbs sampling
- Gibbs sampling $$$\subset$$$ MCMC
- MC
- all samples are independent
- probability of sample chosen is random
- MCMC
- It is based on "Markov Chain"
- Next sample is affected by current sample
- Gibbs sampling
- It is based on "Markov Chain"
- Next sample is affected by current sample
- Preserves all variables but it affects "only one variable"
================================================================================
Example of Gibbs sampling
- Joint probability distribution of 3 random variables
$$$p(x_1,x_2,x_3)$$$
- You want to create "one sample" from that joint probability distribution
================================================================================
Let's do above sampling by using Gibbs sampling
- Make one ramdom sample, $$$X^0 = (x_1^0,x_2^0,x_3^0)$$$
- Change only one random variable (like $$$X_1$$$)
and make next new sample $$$X^1$$$
- When you use sample, you throw away $$$X^0$$$ and you will use only $$$X^1$$$
================================================================================
Let's see more detail about following step
/ Change only one random variable (like $$$X_1$$$) /
/ and make next new sample $$$X^1$$$ /
- Fix 2 random variables' value $$$x_2^0,x_3^0$$$ from give sample $$$X^{0}$$$
- Create new $$$x_1^1$$$ based on following probability, $$$p(x_1^1|x_2^0,x_3^0)$$$
- Fix 2 random variables' value $$$x_1^1,x_3^0$$$ from give sample $$$X^{0}$$$
- Create new $$$x_2^1$$$ based on following probability, $$$p(x_2^1|x_1^1,x_3^0)$$$
- Fix 2 random variables' value $$$x_1^1,x_2^1$$$ from give sample $$$X^{0}$$$
- Create new $$$x_3^1$$$ based on following probability, $$$p(x_3^1|x_1^1,x_2^1)$$$
- You get final $$$X^1$$$ as $$$X^1 = (x_1^1,x_2^1,x_3^1)$$$
================================================================================
Conditional probability like $$$p(x_1^1|x_2^0,x_3^0)$$$ is proportinal
to joint probability distribution $$$p(x_1,x_2,x_3)$$$
In the initial periods, samples are strongly dependent on initial status $$$X^0$$$
But after you make many sample, initial status becomes no effect
It means you can make sample based on joint probability distribution p
================================================================================
Suppose you want to make samples which follows 2D Gaussian Normal distribution
by using Gibbs sampling
 ================================================================================
- Suppose data which has 3 random variables a,b,c
- Then, you have to make sample 3 times
- Fix: b,c, Extract: a
- Fix: a,c, Extract: b
- Fix: a,b, Extract: c
================================================================================
There are variants of "Gibbs sampling"
- Block Gibbs sampling (extract something in group)
- Fix: c, Extract: a,b
- Fix: a,b, Extract: c
- Collapsed Gibbs sampling (remove useless random variable)
- Remove: b, Fix: c, Extract: a
- Remove: b, Fix: a, Extract: c
================================================================================
Code
Gibbs sampling
- Start from x or y
- Iterate p(y|x) and p(x|y)
- Based on above conditional probability, select samples
- Output sample x and y becomes approximated sample
which can be obtained from joint probability distribution of x and y
================================================================================
Problem definition
- Roll the 2 dices
- Value of the first dice is x, sum value of the 2 dices is y
- Think of joint probability of x and y
================================================================================
import random
def roll_a_die():
# Value of the dice is {1,2,3,4,5,6}
# Each value has same probability of chosen (uniform distribution)
# Return one value from {1,2,3,4,5,6}
return random.choice(range(1,7))
================================================================================
def direct_sample():
# Value 1
d1 = roll_a_die()
# Value 2
d2 = roll_a_die()
x=d1
y=d1+d2
return x, y
================================================================================
# Calculate p(y|x)
def random_y_given_x(x):
given_condition=x
variable_y=roll_a_die()
new_y=given_condition+variable_y
return new_y
# Calculate p(x|y)
def random_x_given_y(y):
given_condition=y
if given_condition <= 7:
return random.randrange(1, y)
else:
return random.randrange(y-6, 7)
================================================================================
# Gibbs sampling function
def gibbs_sample(num_iters=100):
# Random initial values
x, y = 1, 2
================================================================================
for _ in range(num_iters):
# Fix: y, Extract: x
x = random_x_given_y(y)
# Fix: x, Extract: y
y = random_y_given_x(x)
return x, y
================================================================================
- Suppose data which has 3 random variables a,b,c
- Then, you have to make sample 3 times
- Fix: b,c, Extract: a
- Fix: a,c, Extract: b
- Fix: a,b, Extract: c
================================================================================
There are variants of "Gibbs sampling"
- Block Gibbs sampling (extract something in group)
- Fix: c, Extract: a,b
- Fix: a,b, Extract: c
- Collapsed Gibbs sampling (remove useless random variable)
- Remove: b, Fix: c, Extract: a
- Remove: b, Fix: a, Extract: c
================================================================================
Code
Gibbs sampling
- Start from x or y
- Iterate p(y|x) and p(x|y)
- Based on above conditional probability, select samples
- Output sample x and y becomes approximated sample
which can be obtained from joint probability distribution of x and y
================================================================================
Problem definition
- Roll the 2 dices
- Value of the first dice is x, sum value of the 2 dices is y
- Think of joint probability of x and y
================================================================================
import random
def roll_a_die():
# Value of the dice is {1,2,3,4,5,6}
# Each value has same probability of chosen (uniform distribution)
# Return one value from {1,2,3,4,5,6}
return random.choice(range(1,7))
================================================================================
def direct_sample():
# Value 1
d1 = roll_a_die()
# Value 2
d2 = roll_a_die()
x=d1
y=d1+d2
return x, y
================================================================================
# Calculate p(y|x)
def random_y_given_x(x):
given_condition=x
variable_y=roll_a_die()
new_y=given_condition+variable_y
return new_y
# Calculate p(x|y)
def random_x_given_y(y):
given_condition=y
if given_condition <= 7:
return random.randrange(1, y)
else:
return random.randrange(y-6, 7)
================================================================================
# Gibbs sampling function
def gibbs_sample(num_iters=100):
# Random initial values
x, y = 1, 2
================================================================================
for _ in range(num_iters):
# Fix: y, Extract: x
x = random_x_given_y(y)
# Fix: x, Extract: y
y = random_y_given_x(x)
return x, y

