https://www.youtube.com/watch?v=GVPTGq53H5I
================================================================================

 ================================================================================
================================================================================
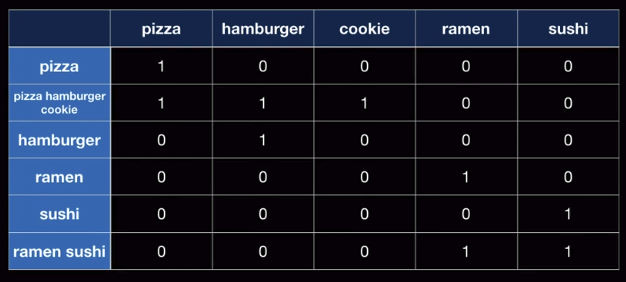 - Let's use bag of word
- Meaning
- pizza and hamburger are US food
- cosine_similarity(pizza,hamburger)=0
- cosine_similarity is dot product of pizza vector ([1,0,0,0,0]) and hamburger vector ([0,1,0,0,0])
- cosine_similarity(pizza,ramen)=0
- cosine_similarity(pizza,hamburger)=0 doesn't make sense
================================================================================
Let's perform same task by using TF-IDF
But you will get same incorrect similarity result
================================================================================
Why this incorrect result occurs?
It's because bag of word and TF-IDF are word-based vectors
It means you can't find any topic from the word,
so you get 0 similarity
================================================================================
LSA can find similarity based on "topic"
================================================================================
Word-document matrix
- Let's use bag of word
- Meaning
- pizza and hamburger are US food
- cosine_similarity(pizza,hamburger)=0
- cosine_similarity is dot product of pizza vector ([1,0,0,0,0]) and hamburger vector ([0,1,0,0,0])
- cosine_similarity(pizza,ramen)=0
- cosine_similarity(pizza,hamburger)=0 doesn't make sense
================================================================================
Let's perform same task by using TF-IDF
But you will get same incorrect similarity result
================================================================================
Why this incorrect result occurs?
It's because bag of word and TF-IDF are word-based vectors
It means you can't find any topic from the word,
so you get 0 similarity
================================================================================
LSA can find similarity based on "topic"
================================================================================
Word-document matrix
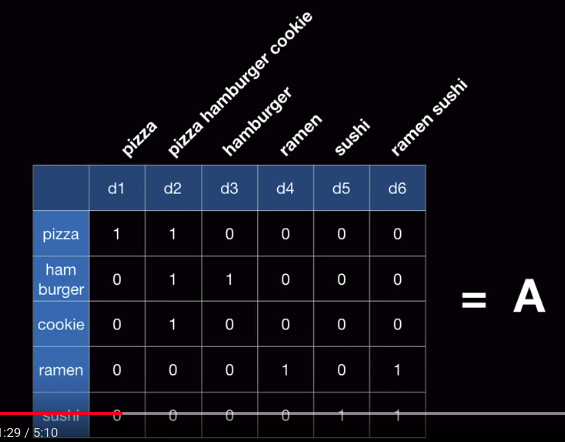 Words in y axis: individual words
Elements in x axis: 6 sentences
Let's call above 2D array as A
================================================================================
Perform singular vector decomposition
$$$A \approx U \times \Sigma \times V^t$$$
Words in y axis: individual words
Elements in x axis: 6 sentences
Let's call above 2D array as A
================================================================================
Perform singular vector decomposition
$$$A \approx U \times \Sigma \times V^t$$$
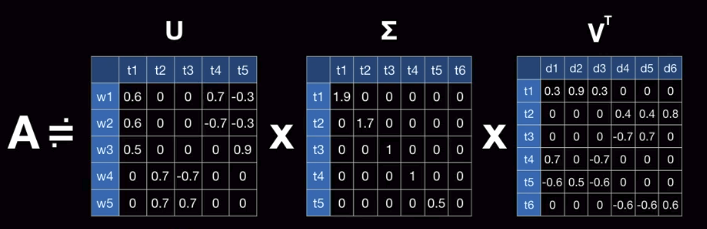 ================================================================================
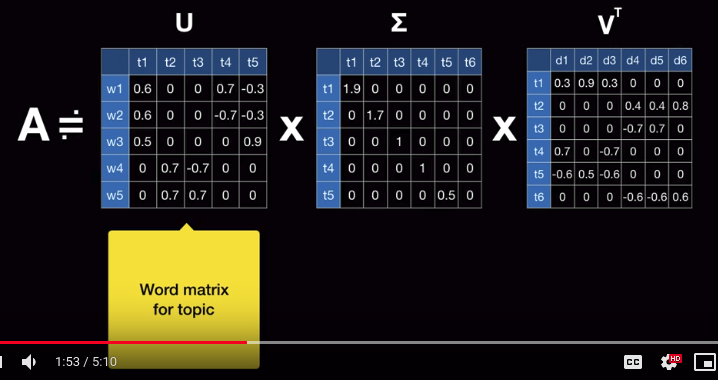
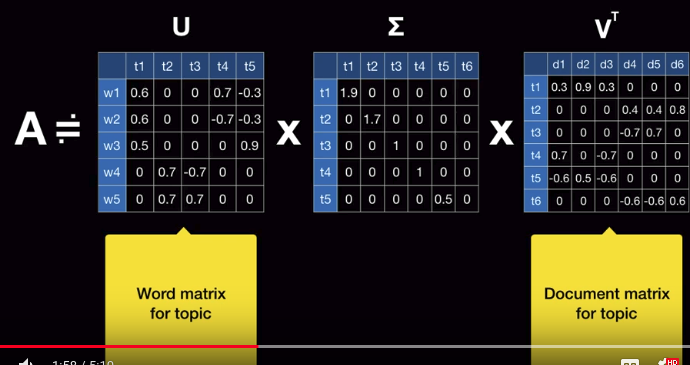
$$$U$$$ can be considered as "word matrix" for topic
================================================================================
$$$U$$$ can be considered as "word matrix" for topic
 ================================================================================
$$$V^T$$$ can be considered as "document (or sentence) matrix" for topic
================================================================================
$$$V^T$$$ can be considered as "document (or sentence) matrix" for topic
 ================================================================================
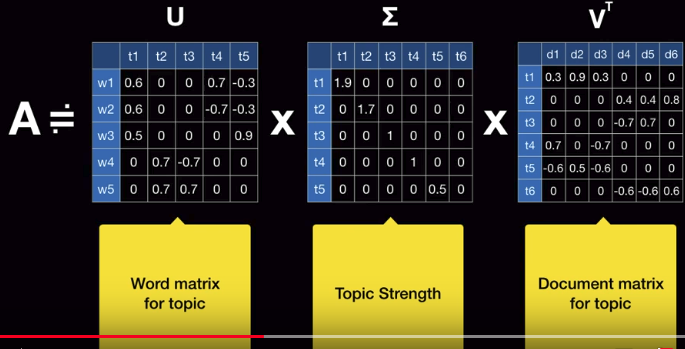
$$$\Sigma$$$ can be considered as "strength matrix" for topic
================================================================================
$$$\Sigma$$$ can be considered as "strength matrix" for topic
 ================================================================================
================================================================================
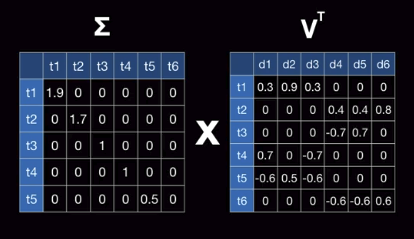 What you are interested in "document (or sentence) matrix" for topic
So, multiply "strength" by "document (or sentence) matrix" for topic
================================================================================
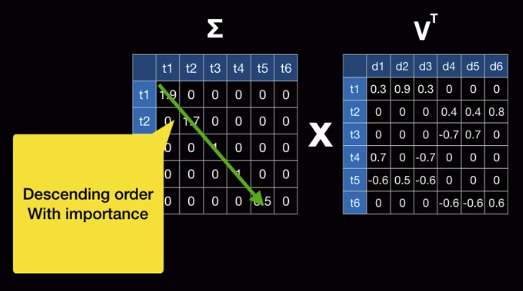
Due to characteristic of $$$\Sigma$$$,
diagonal elements are descending order which has importance
What you are interested in "document (or sentence) matrix" for topic
So, multiply "strength" by "document (or sentence) matrix" for topic
================================================================================
Due to characteristic of $$$\Sigma$$$,
diagonal elements are descending order which has importance
 ================================================================================
For simplicity, select 2 importances: t1 and t2
================================================================================
For simplicity, select 2 importances: t1 and t2
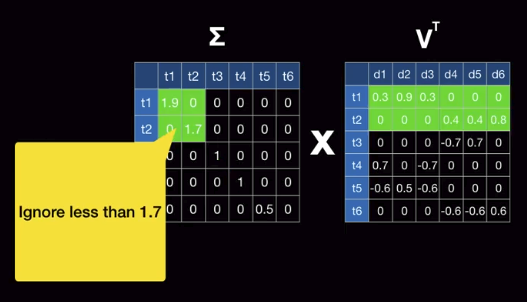 $$$(2,2) \cdot (2,6) = (2,6)$$$
================================================================================
Actual result
$$$(2,2) \cdot (2,6) = (2,6)$$$
================================================================================
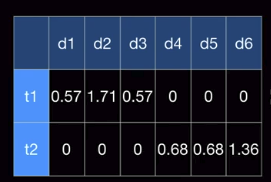
Actual result
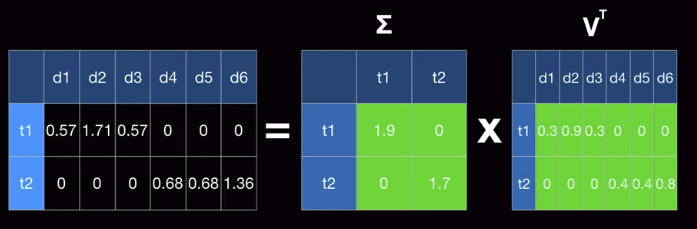 ================================================================================
Let's plot this table on 2D space
================================================================================
Let's plot this table on 2D space
 ================================================================================
Result
================================================================================
Result
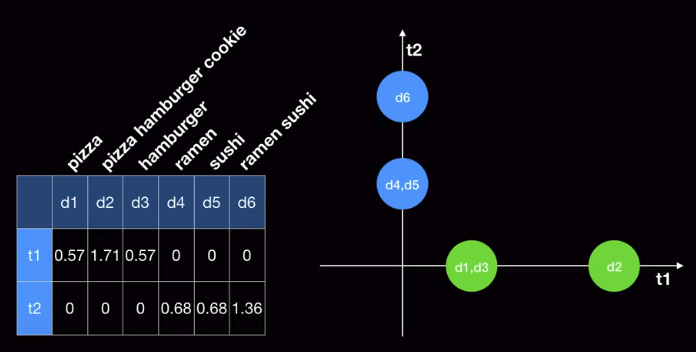 ================================================================================
Let's calculate cosine similarities
cosine_similarity(d1,d2)=1
cosine_similarity(d1,d3)=1
cosine_similarity(d2,d3)=1
Max of cosine_similarity is 1
Max similarity
================================================================================
================================================================================
Let's calculate cosine similarities
cosine_similarity(d1,d2)=1
cosine_similarity(d1,d3)=1
cosine_similarity(d2,d3)=1
Max of cosine_similarity is 1
Max similarity
================================================================================
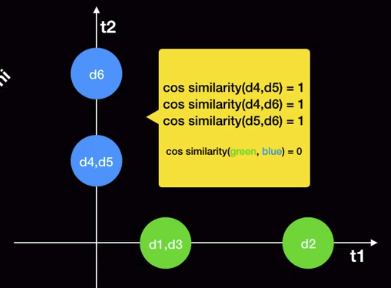 cosine_similarity(d4,d5)=1
cosine_similarity(d4,d6)=1
cosine_similarity(d5,d6)=1
Max of cosine_similarity is 1
Max similarity
================================================================================
cosine_similarity(d4,d5)=1
cosine_similarity(d4,d6)=1
cosine_similarity(d5,d6)=1
Max of cosine_similarity is 1
Max similarity
================================================================================
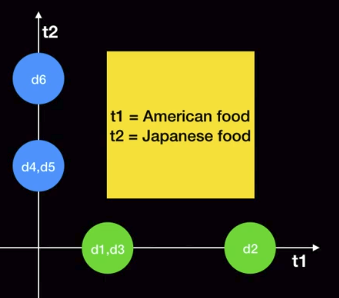 Conclusion
- You can know the latent semantic of 2 axes
================================================================================
Conclusion
- You can know the latent semantic of 2 axes
================================================================================
 d2 has more strength
But cosine similarity ignores strength so that you get 1 from both circles
================================================================================
d2 has more strength
But cosine similarity ignores strength so that you get 1 from both circles
================================================================================
















