Notes that I wrote as I was taking a video lecture originated from
https://www.youtube.com/watch?v=oBw_176vH6k
Key points
================================================================================
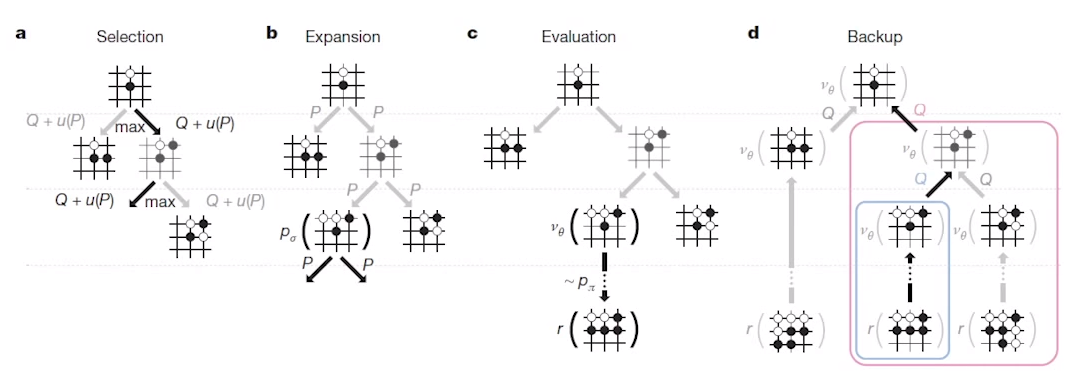 Search is composed of 4 steps
1. Selection
2. Expansion
3. Evaluation
4. Backup
================================================================================
Node: state
Edge : action
After action, agent goes to next node (state)
This structure has tree shape
================================================================================
Selection: tree is created, which is started from the root state (root node)
- "Selection" is to select where agent should go, and agent goes to down "with selecting"
- Top state: Root state
- At first, there is only root node.
- But after some time, tree will be generated
- Then, agent should go from root node to leaf node (which doesn't have its child node)
Agent goes to there (leaf node) with selecting eahc node
- When "selecting",
you should consider
"how many times you had that decision"
"how good that decision was"
to go to up to leaf node
- My comments:
(1) Suppose there is one stone on the grid floor.
That would be root node.
(2) Suppose play went to "10 times of putting stones"
Node which represents 10th putting stone can be considered as leaf node.
================================================================================
Expanson
- As soon as agent reaches to "leaf node",
computer puts the one more stone by using "SL policy"
- Then, one branch is created
================================================================================
Evaluation
- Then, you should evaluate that "expanded node"
- For example, you can get 60% probability of winning the game due to that "expanded node"
- And that 60% probability (which represents how good that expanded node is) is stored into edges(?)
================================================================================
How you can evaluate in detail?
- Method1:
You use value function
because value function outputs "one sclaar number"
which represents the probability of winning the game
- Method2:
You use rollout policy to play game up to end in various scenarios
- Paper author of AlphaGo said combination (0.5:0.5) of 1 and 2 was best.
- For example, say value function says 0.8 winning rate for black stone.
Say rollout policy says black stone will win.
You average on 0.8 and 1 ($$$(0.8+1)/2=0.9$$$)
0.9 is evaluated score to that "expanded node"
================================================================================
When you evaluate "expanded node",
you actually and implicitly evaluate all edges agent goes through
================================================================================
And back to the "selection",
you can "select" good path based on evaluated node and edge
================================================================================
Summary:
There are good paths and bad paths
In selection step, agent should go along good paths.
Values which represent good and bad paths are updated in more precisely in "backup stage"
================================================================================
Summary2:
1. Selection stage.
- Agent starts in root node.
- Agent selects one path (vertical 3 stages is one path?, and vertical left-next states is second path?
and agent selects one path from them?)
- and Agnet goes to leaf node
2. Expansion stage
- Put one stone more using SL policy
- Make tree deeper
3. Evaluation stage
- Evaluate "expanded node (stone which had been put)"
- To evaluate, use combination of
rollout policy (50%, fast, less accurate, more domain knowledge features)
and value function (50%, create one scalar number value
representing winning probability from entire game)
4. Backup stage
- After evaluation on one new expanded node,
path which is used to reach new expanded node is updated
Monte Carlo Tree Search: iterate 1, 2, 3, 4
If you iterate 1, 2, 3, 4, tree grows bigger and bigger, resulting in more and more accurate evaluation
================================================================================
How to select node in detail
Search is composed of 4 steps
1. Selection
2. Expansion
3. Evaluation
4. Backup
================================================================================
Node: state
Edge : action
After action, agent goes to next node (state)
This structure has tree shape
================================================================================
Selection: tree is created, which is started from the root state (root node)
- "Selection" is to select where agent should go, and agent goes to down "with selecting"
- Top state: Root state
- At first, there is only root node.
- But after some time, tree will be generated
- Then, agent should go from root node to leaf node (which doesn't have its child node)
Agent goes to there (leaf node) with selecting eahc node
- When "selecting",
you should consider
"how many times you had that decision"
"how good that decision was"
to go to up to leaf node
- My comments:
(1) Suppose there is one stone on the grid floor.
That would be root node.
(2) Suppose play went to "10 times of putting stones"
Node which represents 10th putting stone can be considered as leaf node.
================================================================================
Expanson
- As soon as agent reaches to "leaf node",
computer puts the one more stone by using "SL policy"
- Then, one branch is created
================================================================================
Evaluation
- Then, you should evaluate that "expanded node"
- For example, you can get 60% probability of winning the game due to that "expanded node"
- And that 60% probability (which represents how good that expanded node is) is stored into edges(?)
================================================================================
How you can evaluate in detail?
- Method1:
You use value function
because value function outputs "one sclaar number"
which represents the probability of winning the game
- Method2:
You use rollout policy to play game up to end in various scenarios
- Paper author of AlphaGo said combination (0.5:0.5) of 1 and 2 was best.
- For example, say value function says 0.8 winning rate for black stone.
Say rollout policy says black stone will win.
You average on 0.8 and 1 ($$$(0.8+1)/2=0.9$$$)
0.9 is evaluated score to that "expanded node"
================================================================================
When you evaluate "expanded node",
you actually and implicitly evaluate all edges agent goes through
================================================================================
And back to the "selection",
you can "select" good path based on evaluated node and edge
================================================================================
Summary:
There are good paths and bad paths
In selection step, agent should go along good paths.
Values which represent good and bad paths are updated in more precisely in "backup stage"
================================================================================
Summary2:
1. Selection stage.
- Agent starts in root node.
- Agent selects one path (vertical 3 stages is one path?, and vertical left-next states is second path?
and agent selects one path from them?)
- and Agnet goes to leaf node
2. Expansion stage
- Put one stone more using SL policy
- Make tree deeper
3. Evaluation stage
- Evaluate "expanded node (stone which had been put)"
- To evaluate, use combination of
rollout policy (50%, fast, less accurate, more domain knowledge features)
and value function (50%, create one scalar number value
representing winning probability from entire game)
4. Backup stage
- After evaluation on one new expanded node,
path which is used to reach new expanded node is updated
Monte Carlo Tree Search: iterate 1, 2, 3, 4
If you iterate 1, 2, 3, 4, tree grows bigger and bigger, resulting in more and more accurate evaluation
================================================================================
How to select node in detail
 - You should remember you record all scores in path (root node to leaf node (last expanded node))
- Q(s,a): record all scores
- Each edge has Q(S,A), N(S,A), P(S,A)
- Q(S,A): updated scores in path (root node to leaf node (last expanded node)) via backup stage
- N(S,A): how many edge does the agent go thorugh
For example, agent can go through edge1 1 time
For example, agent can go through edge1 0 time
For example, agent can go through edge1 10 times
- $$$P(S,A)$$$: prior probability
SL policy
================================================================================
Agent will use Q, N, P to select node
Agent should select edge (action) which make maximum value for Q+u in selection stage
$$$a_t=\arg_{a}\max ( Q(s_t,a) + u(s_t,a) )$$$
- $$$u(s_t,a) \propto \dfrac{P(s,a)}{1+N(s,a)}$$$
- At first of creating tree, N is small
If N is 0, u is used as P (SL policy value)
It means how SL policy evaluates edge (in other words, P) is used
At first, SL policy affects much to selection action a
- As N becomes larger, u become smaller, Q (average of evaluations) becomes larger
================================================================================
Philosophy of selecting action a
At first, agent goes along guide of SL policy
If agent has enough tree structure, effect of SL policy becomes smaller,
node is selected based on information which informs good place which agent had been through
================================================================================
V: evaluation
v: value function
$$$\lambda_{z_L}$$$: result which agent gets by simulating entire game.
- $$$Q(s,a) = \dfrac{1}{N(s,a)} \sum\limits_{i=1}^{n} 1(s,a,i)V(s_{l}^i)$$$
Weighted sum, average
- $$$\lambda = 0.5$$$ is empirically optimal representing 50:50 (value function:rollout)
- $$$V_{s_L}$$$ is scalar number score value
$$$V_{s_L}$$$ is used on $$$Q(s,a)$$$ from $$$i=1$$$ to 10 if $$$n = 10$$$
Calculated Q is Q value to that edge
================================================================================
Summary
you select action using $$$\arg_{a}\max(Q+u)$$$
you perform expansion (add node) using SL policy
you evaluate expanded node using "rollout and value function"
Based on evaluated scores, you update node and edges located in paths agent went through
Above loop is one loop, you should perform millions of loop
================================================================================
If you perform above cycle for 1 time, you get one large tree
From that large tree, your goal is to select edge (action) having hightest Q
================================================================================
SL policy
Used for expansion because you put one more stone
u includes p, p is from SL policy
================================================================================
Rollout policy
used for evaluation
================================================================================
Value function
used for evaluation along with rollout policy
================================================================================
Why don't places which use SL policy use RL policy (because you said RL policy is more powerful)
RL policy is not directly used for MCTS, RL policy is used to make better value function.
RL policy performs self-play to train value function.
Again, why don't places which use SL policy use RL policy (because you said RL policy is more powerful)
Paper says SL policy was better empirically
================================================================================
The reason is that
SL policy uses dataset which is maded from tons of various Go match records performed by various players
So, decision of SL policy doesn't converge to specific area
In other words, decision of SL policy is more generallized, with exploiting various states.
If you use RL policy, since RL policy reinforces best path,
decision of RL policy becomes more specific and narrow and biased.
================================================================================
Training method.
Update "policy network A" over 500 bathes
policy network A becomes stronger
Developers create "opponent pool"
You put "weak policy network A (before trained)" and "policy network B" into "opponent pool"
You randomly select one policy network from opponent pool
You perform RL with "strong policy network A" and "randomly selected policy network"
You put better policy network into opponent pool (now there are 3 policy network)
And you randomly select one policy network and perform RL
================================================================================
Why do this instead you use just strong-strong policy network continuously?
It causes non-generalized solution (overfitting to one policy (not generalized various policy)).
- You should remember you record all scores in path (root node to leaf node (last expanded node))
- Q(s,a): record all scores
- Each edge has Q(S,A), N(S,A), P(S,A)
- Q(S,A): updated scores in path (root node to leaf node (last expanded node)) via backup stage
- N(S,A): how many edge does the agent go thorugh
For example, agent can go through edge1 1 time
For example, agent can go through edge1 0 time
For example, agent can go through edge1 10 times
- $$$P(S,A)$$$: prior probability
SL policy
================================================================================
Agent will use Q, N, P to select node
Agent should select edge (action) which make maximum value for Q+u in selection stage
$$$a_t=\arg_{a}\max ( Q(s_t,a) + u(s_t,a) )$$$
- $$$u(s_t,a) \propto \dfrac{P(s,a)}{1+N(s,a)}$$$
- At first of creating tree, N is small
If N is 0, u is used as P (SL policy value)
It means how SL policy evaluates edge (in other words, P) is used
At first, SL policy affects much to selection action a
- As N becomes larger, u become smaller, Q (average of evaluations) becomes larger
================================================================================
Philosophy of selecting action a
At first, agent goes along guide of SL policy
If agent has enough tree structure, effect of SL policy becomes smaller,
node is selected based on information which informs good place which agent had been through
================================================================================
V: evaluation
v: value function
$$$\lambda_{z_L}$$$: result which agent gets by simulating entire game.
- $$$Q(s,a) = \dfrac{1}{N(s,a)} \sum\limits_{i=1}^{n} 1(s,a,i)V(s_{l}^i)$$$
Weighted sum, average
- $$$\lambda = 0.5$$$ is empirically optimal representing 50:50 (value function:rollout)
- $$$V_{s_L}$$$ is scalar number score value
$$$V_{s_L}$$$ is used on $$$Q(s,a)$$$ from $$$i=1$$$ to 10 if $$$n = 10$$$
Calculated Q is Q value to that edge
================================================================================
Summary
you select action using $$$\arg_{a}\max(Q+u)$$$
you perform expansion (add node) using SL policy
you evaluate expanded node using "rollout and value function"
Based on evaluated scores, you update node and edges located in paths agent went through
Above loop is one loop, you should perform millions of loop
================================================================================
If you perform above cycle for 1 time, you get one large tree
From that large tree, your goal is to select edge (action) having hightest Q
================================================================================
SL policy
Used for expansion because you put one more stone
u includes p, p is from SL policy
================================================================================
Rollout policy
used for evaluation
================================================================================
Value function
used for evaluation along with rollout policy
================================================================================
Why don't places which use SL policy use RL policy (because you said RL policy is more powerful)
RL policy is not directly used for MCTS, RL policy is used to make better value function.
RL policy performs self-play to train value function.
Again, why don't places which use SL policy use RL policy (because you said RL policy is more powerful)
Paper says SL policy was better empirically
================================================================================
The reason is that
SL policy uses dataset which is maded from tons of various Go match records performed by various players
So, decision of SL policy doesn't converge to specific area
In other words, decision of SL policy is more generallized, with exploiting various states.
If you use RL policy, since RL policy reinforces best path,
decision of RL policy becomes more specific and narrow and biased.
================================================================================
Training method.
Update "policy network A" over 500 bathes
policy network A becomes stronger
Developers create "opponent pool"
You put "weak policy network A (before trained)" and "policy network B" into "opponent pool"
You randomly select one policy network from opponent pool
You perform RL with "strong policy network A" and "randomly selected policy network"
You put better policy network into opponent pool (now there are 3 policy network)
And you randomly select one policy network and perform RL
================================================================================
Why do this instead you use just strong-strong policy network continuously?
It causes non-generalized solution (overfitting to one policy (not generalized various policy)).

