This is notes which I wrote as I was taking a video lecture which is originated from https://www.youtube.com/watch?v=Vd-gmo-qO5E&list=PLlMkM4tgfjnKsCWav-Z2F-MMFRx-2gMGG&index=5 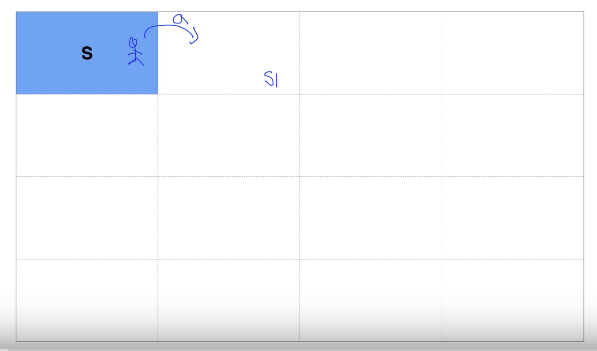================================================================================ - At S, agent knows only S. - After agent does action of moving right, environment gives agent "state" you're in state S1 ================================================================================ - When agent moves right, environment give "reward 0" to the "agent" - When agent reaches to goal place, environment gives agent reward 1 - When agent falls into the hole, environment gives agent reward -1 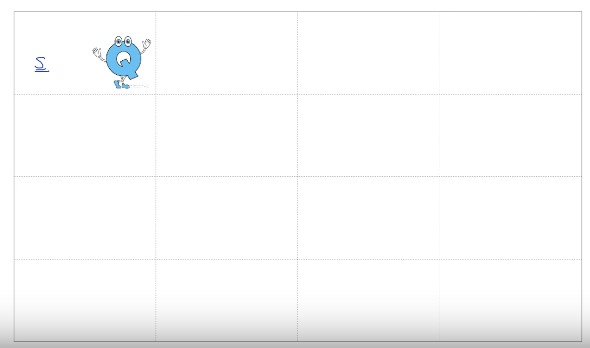================================================================================ - Suppose agent is in s (top left) - Suppose there is Q mentor - And agent asks Q mentor that where I should go to from the options; left, right, top, bottom. ================================================================================ - Q mentor says "I know every good and bad paths because I have walked through all paths (L,R,U,D) at state s" Q mentor says if you go to right, you will get 0.5 score Q mentor says if you go to bottom, you will get 0.3 score ================================================================================ Q-function State-action value function Q(state,action) Input to Q: state (agent is being in) and action (agent would like to do) Output from Q: quality wrt given state and action ================================================================================ - There is Q mentor at s1 - Agent asks where I should go to to Q-mentor-staying-at-s1 - Q-mentor-staying-at-s1 says scores; 0, 0.5, 0, 0.3 - Agent finds 1. maximum value (0.5), 2. argument of maximum value (2 index) - Agent moves to right using "index number 2" ================================================================================ $$$\max_a Q(s_1,a)$$$ $$$\max Q(s_1,a) = 0.5$$$ Variable which agent is interested in is action a, so you should write like this $$$\max_a Q(s_1,a)$$$ it means max value from $$$Q(s_1,a)$$$ by manipulating variable action a ================================================================================ "Argument a" when Q is maximum $$$\arg_a \max Q(s_1,a) \rightarrow \text{Index 2: RIGHT}$$$ ================================================================================ Policy is represented generally by $$$\pi$$$ $$$\pi^{*}(s) = \arg_a \max Q(s,a)$$$ $$$\pi^{*}$$$: optimal policy It means argument a which has max Q Actions: left, right, bottom, up Policy: $$$\pi^{*}(s) = \arg_a \max Q(s,a)$$$ for example, "go right" ================================================================================ So far, you just supposed there would be Q mentor Then, you should have a question about how you can train that Q mentor to make Q mentor to say more precise guide for the agent? ================================================================================ This is the sentence which you just should believe as kind of axiom "When agent is at state s, there is Q mentor at $$$s^{'}$$$ state, and Q mentor knows $$$Q(s^{'},a^{'})$$$" ================================================================================ - Agent will do "action a" - Then, agent will go to "state $$$s^{'}$$$" - And agent will get "reward r" at state s from the environment - What you would like to know is $$$Q(s,a)$$$ (when agent is at s, when agent would like to do action a, what is the Q value?) - Again, you should just believe following sentence "There is Q mentor at $$$s^{'}$$$, and Q mentor knows $$$Q(s^{'},a^{'})$$$" - Then, your question is how can you express $$$Q(s,a)$$$ by using $$$Q(s^{'},a^{'})$$$? ================================================================================ - Suppose agent is at state s - What you would like to know is $$$Q(s,a)$$$ at state s - If agent does "action a", agent gets state $$$s^{'}$$$ and reward r - You supposed Q mentor knows $$$Q(s^{'},a^{'})$$$ at state $$$s^{'}$$$ - At state $$$s^{'}$$$, there are 2 values: r and $$$Q(s^{'},a^{'})$$$ - And those r and $$$Q(s^{'},a^{'})$$$ are related to $$$Q(s,a)$$$ because agent went to $$$s^{'}$$$ based on $$$\arg_a \max Q(s^{'},a^{'})$$$ - So, you can write $$$Q(s,a)=r+\max Q(s^{'},a^{'})$$$ ================================================================================ $$$s_0$$$: state at time 0 $$$a_0$$$: action at time 0 $$$r_1$$$: reward at time 1 $$$s_1$$$: state at time 1 $$$a_1$$$: action at time 1 $$$r_2$$$: reward at time 2 $$$s_2$$$: state at time 2 $$$a_2$$$: action at time 2 ... $$$r_{n-1}$$$: reward at time n-1 $$$s_{n-1}$$$: state at time n-1 $$$a_{n-1}$$$: action at time n-1 $$$r_{n}$$$: reward at time n $$$s_{n}$$$: state at time n (terminal state) ================================================================================ What agent is interested in is reward - Especially, let's think of future reward - Future reward is sum of all rewards Sum of all rewards $$$R=r_1+r_2+r_3+\cdots+r_n$$$ - Let's think of future reward at time t $$$R_t = r_t + r_{t+1} + r_{t+2} + \cdots + r_{n}$$$ - Let's think of future reward at time t+1 $$$R_t = r_{t+1} + r_{t+2} + \cdots + r_{n}$$$ - Note that there is duplicated part $$$r_{t+1} + r_{t+2} + \cdots + r_{n}$$$ - So, you can write like this: $$$R_t = r_t + R_{t+1}$$$ - Let's suppose $$$r_{t+1} + r_{t+2} + \cdots + r_{n}$$$ is optimal reward which is maximal reward agent can obtain - Then, you can write: $$$R^{*}_t= r_t +\max R_{t+1}$$$ ================================================================================ Abvoe equation becomes identical form to function which learns Q function; $$$Q(s,a)=r+\max_{a^{'}}Q(s^{'},a^{'})$$$ r: reward which agent gets by doing action a ================================================================================ You finally get equation which can update function $$$Q(s,a)$$$ $$$\hat{Q}(s,a) \leftarrow r + \max_{a^{'}} \hat{Q}(s^{'},a^{'})$$$ $$$\hat{Q}(s,a)$$$: Q value at current time $$$r$$$: reward when agent does action a By using $$$r + \max_{a^{'}} \hat{Q}(s^{'},a^{'})$$$, you update $$$\hat{Q}(s,a)$$$ ================================================================================ 16 states 4 actions ================================================================================ - You don't know Q values so you initialize them by 0 ================================================================================ - Let's calculate Q at state s - reward is $$$0$$$ - max Q is 0 from initially initialized $$$0,0,0,0$$$ - $$$Q(s,a)=0+0=0$$$ ================================================================================ - 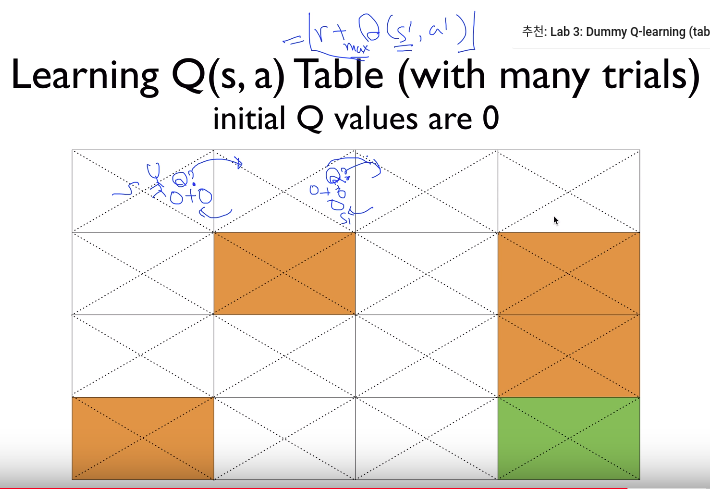Let's calculate Q at state s+1 - $$$Q(s_{t+1},a_{t+1})=0+0=0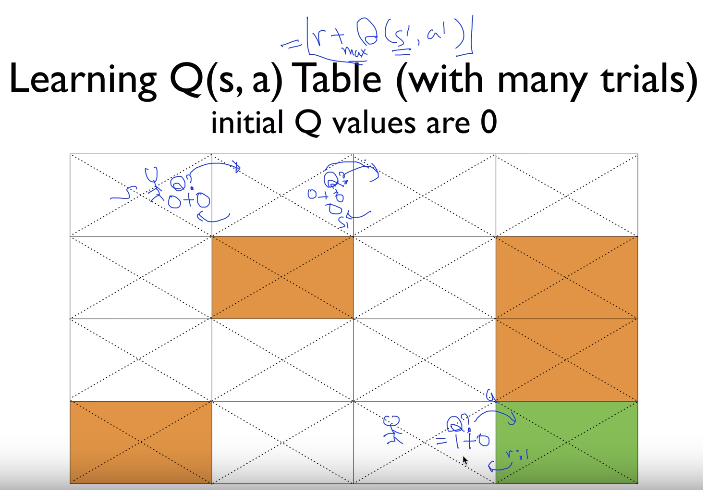$$$ ================================================================================ - Suppose agent is located in left from goal place - That place Q is Q=1+0=1 - Q is updated ================================================================================ 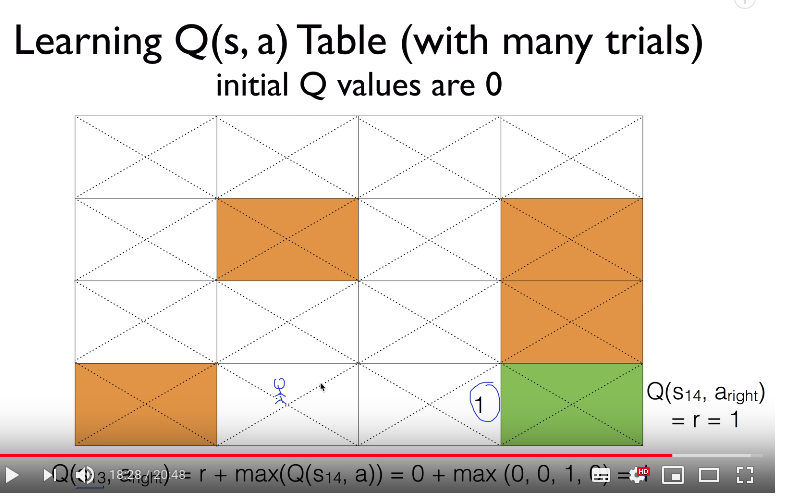Suppose agent is at state 13 Suppose action is right Q=0+1=1 ================================================================================ 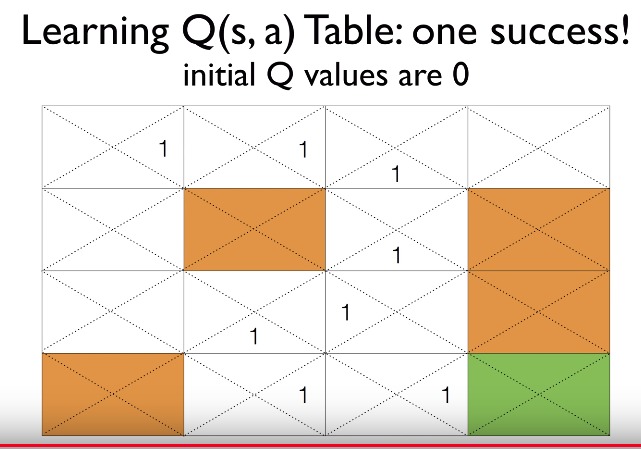Q values at each place can be updated like this ================================================================================ Agent can follow optimal policy at each place to arrive terminating place ================================================================================ Summary - For each "s and a", you initialize table by 0 $$$\hat{Q}(s,a) \leftarrow 0$$$ - Observe current state s from environment - Select action a and execute that action a - Agent gets immediate reward r - Observe new state $$$s^{'}$$$ from $$$s$$$ - Update $$$\hat{Q}(s,a)$$$ by using follow $$$\hat{Q}(s,a) \leftarrow r + \max_{a^{'}} \hat{Q}(s^{'},a^{'})$$$ - Make new state $$$s^{'}$$$ into current state $$$s$$$ - Then, you can get "trained Q"