================================================================================ (100*100*4,) 1D array is needed for 100x100 maze problem using Q table learning - 4: actions (LRUD) ================================================================================ $$$2^{80\times 80}$$$: number of possible screen of right situation Creating $$$(2^{80\times 80},)$$$ 1D array is impossible ================================================================================ Q methodology is good but you can't use Q table for practical problem ================================================================================ - 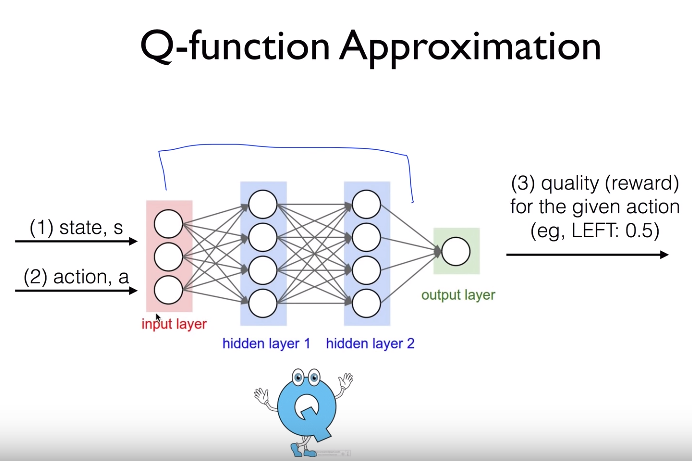Network: takes input, release output - State s and action a can be considered as input - Output from output layer can be considered as Q value of Q mentor - Idea: let's use Q-network instead of Q-table 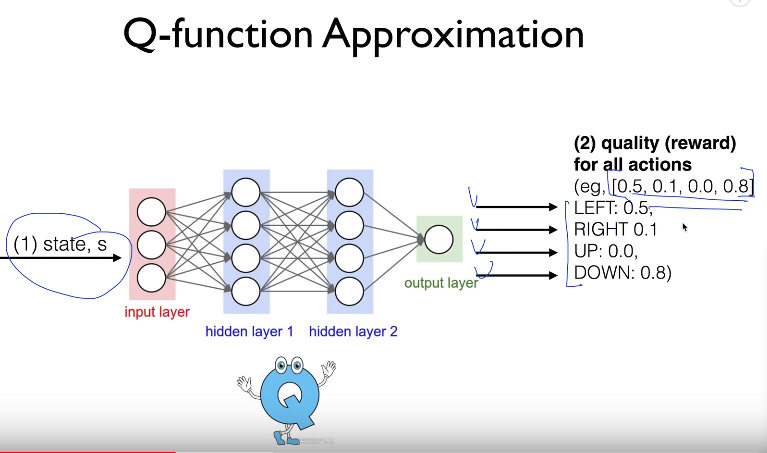================================================================================ - You can variant version of Q-network - Q-network takes state s as input - Q-network outputs 4 length 1D array like [0.5,0.1,0.0,0.8] [0.5,0.1,0.0,0.8] can be considered as Q values to left, right, up, down 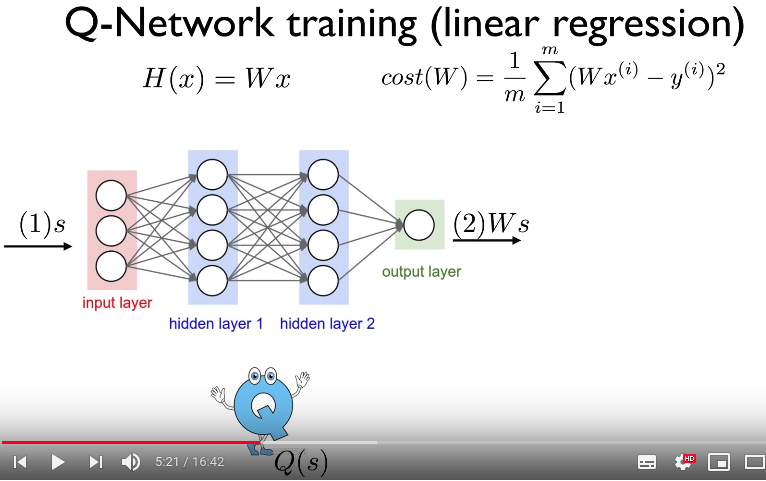================================================================================ - Let's train Q-network as linear regression problem - You training goal is to make Ws become optimal $$$Q$$$ value $$$Q^{*}$$$ - Optimal $$$Q$$$ value $$$Q^{*}$$$ can be considered as label ================================================================================ Model funcion: H(x)=Wx - x: input - W: trainable parameter ================================================================================ Cost function: $$$\text{cost}(W)=\dfrac{1}{m} \sum\limits_{i=1}^{m} (Wx^{(i)} - y^{(i)})^2$$$ $$$Wx^{(i)}$$$: prediction $$$y^{(i)}$$$: label 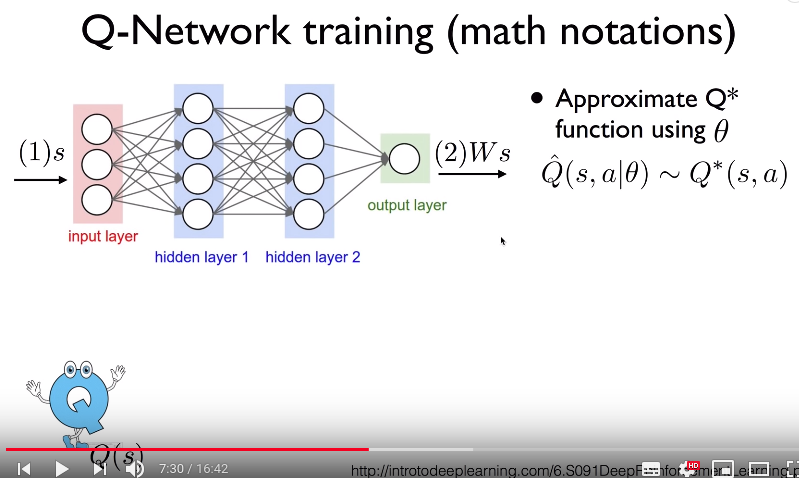================================================================================ - You will replace Ws with $$$\hat{Q}(s,a,|\theta)$$$ -$$$\hat{Q}(s,a,|\theta)$$$: Q is function wrt state s and action a but varying $$$\theta$$$ affect Q and s and a - $$$\theta$$$: trainable parameters in Q-network - Your goal: $$$\hat{Q}$$$ should much approximate optimal $$$Q^{*}$$$ $$$\hat{Q}(s,a|\theta) \sim Q^{*}(s,a)$$$ ================================================================================ How can you make $$$\hat{Q}$$$ much approximate optimal $$$Q^{*}$$$? $$$\min_{\theta} \sum\limits_{t=0}^{T} [ \hat{Q}(s_t,a_t|\theta) - (r_t+\gamma \max_{a^{'}} \hat{Q}(s_{t+1},a^{'}|\theta))]^2$$$ - Minimize difference - By adjusting trainable parameters $$$\theta$$$ ================================================================================ - Initialize...: Randomly initialize trainable parameters in Q-network - Initialise sequence...: create first state $$$s_1$$$ - and preprocessed...: Preprocess state (for example, process image, etc) by using function $$$\phi$$$ - With probability...: exploration using e-greedy to select action $$$a_t$$$ - otherwise select...: expoit - Execute action...: execute action $$$a_t$$$ and get reward and state (like image $$$x_{t+1}$$$) - Set $$$y_{j}$$$...: training part ================================================================================ * $$$y_{j}$$$: label * $$$(y_j - Q(\phi_j,a_j;\theta))$$$: loss function * $$$r_j$$$: reward agent gets at terminal place * $$$r_j + \gamma \max_{a^{'}} Q(\phi_{j+1},a^{'};\theta)$$$: reward agent gets at non-terminal place * $$$(y_j - Q(\phi_j,a_j;\theta))^2$$$.backward() * ADAM_optimizer.step() ================================================================================ Q-network under deterministic and non-deterministic environment * In neural net, you don't use $$$(1-\alpha)Q(s,a) + \alpha [ r+ \gamma \max_{a^{'}} Q(s^{'},a^{'})]$$$ as target $$$y_j$$$ even if env is non-deterministic. * As you can see, you use $$$r_j + \gamma \max_{a^{'}} Q(\phi_{j+1},a^{'};\theta)]$$$ as target $$$y_j$$$ ================================================================================ Will it work? It works because neural network trains "gradually" ================================================================================ * If you minimize difference of pred_Q-target_Q by adjusting $$$\theta$$$ prediction $$$\hat{Q}$$$ converges to $$$Q^{*}$$$? * In neural network, it diverges due to (1) correlations between samples (2) non-stationary targets ================================================================================ Above Q-network issue had been solved by DQN algorithm by DeepMind ================================================================================ DQN (1) deep networks (2) experience replay (3) separated networks