007_lec_DQN.html # https://www.youtube.com/watch?v=S1Y9eys2bdg&list=PLlMkM4tgfjnKsCWav-Z2F-MMFRx-2gMGG&index=14 # @ # In previous lectures, you used Q table algorithm, # which works well in simple way # But since it uses table structure, # it can't solve big and complex problem # @ # So, you tried not to express values in q table, # but to express and approximate values by using q network # You input "state" data into network, # and network outputs reward data (predicted q values) for all actions # @ # $$$\hat{Q}$$$ approximates to Q # $$$\hat{Q}$$$ converges when you use Q table # However, $$$\hat{Q}$$$ diverges when you use Q network due to 2 reasons, # resulting in not efficient training by q network # 1. Correlations between samples # 1. 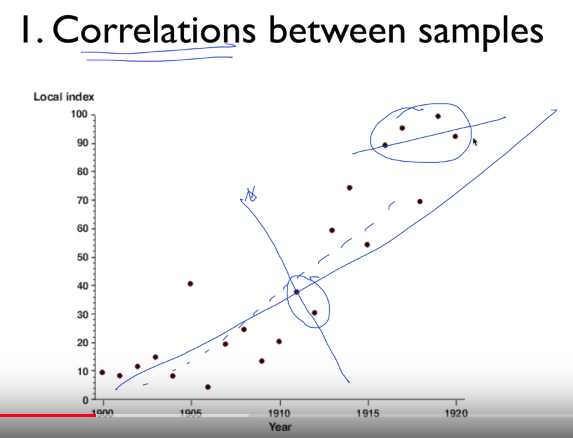Non-stationary targets # @ # Above 2 issues were resolved by deepmind from DQN algorithms(2013, 2015) # @ # Issue 1. Correlations between samples # With 2 samples strongly correlated to each other # With 4 samples strongly correlated to each other # They can create different lines compared to target line # img 2018-04-29 11-37-10.png # # @ # Issue 2. Non-stationary targets (moving target) # y label (target) = $$$r_{t}+\gamma max_{a'} \hat{Q}(s_{t+1},a'|\theta)$$$ # prediction of Q or $$$\hat{y} = \hat{Q}(s_{t},a_{t}|\theta)$$$ # You should make them (target y, prediction Q) almost same # For this, you should make prediction Q near to target y # In other words, you update network (update parameter $$$\theta$$$), # for $$$Q = \hat{Q}(s_{t},a_{t}|\theta)$$$ # But in this case, You should know above 2 terms (target y, prediction Q), # runing in same network with same parameter $$$\theta$$$ # With this condition, automatically and inevitably, # target y = $$$r_{t}+\gamma max_{a'} \hat{Q}(s_{t+1},a'|\theta)$$$ becomes to move by moved $$$\hat{y}$$$ # because they use same network and same parameter $$$\theta$$$ # In summary, changing parameter in prediction Q network leads to moving target y # @ # DQN's three solutions for above issues # 1. Go deep to refrect various state # (multiple layers = convolution layers + pooling layers + fully connected layers + ...) # 1. Captrue and replay ("experience replay" way) # for "correlation between samples" issue # You perform loop with giving "action", # and you obtain "state" # At this moment, you don't start training, # but you store values (state,action,reward,...) into buffer # After enough time, you extract values randomly, # and start training with them # 1. Separate networks: in other words, you create a target network # for "non-stationary target" issue # @ # It's bad idea to train with samples having strong correlations # You can use "experience replay" to resolve this issue # You iterate following steps, obtain "action", from "action" obtain "state" # At this time of iteration, don't train (weights), but store actions and states into buffter # Then, you extract several values randomly from buffer # You train model with them # img 2018-04-29 12-35-17.png # # @ # You store actions, rewards, states into buffer D # You extract samples randomly from buffer D, # and you create mini batch with them, # and you train model with those batches # img 2018-04-29 12-37-43.png # # @ # Why does above technique work? 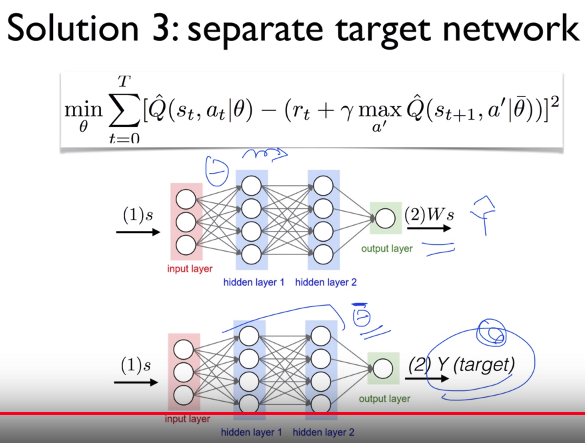# Key is "you extract sample randomly", # which can reflect distribution of entire data, # with avoiding extracting strongly correlated samples # img 2018-04-29 12-40-11.png # # @ # You will use two separated parameters $$$\theta$$$ and $$$\bar{\theta}$$$, # which means you use separated different network for y and $$$\hat{y}$$$ # You won't use second formular in following illustration, # which has only one $$$\theta$$$ for both y and $$$\hat{y}$$$ # Step: # You bring label y from second term, # and you stay it, # and you update first term # img 2018-04-29 12-45-50.png # # img 2018-04-29 12-46-42.png # # 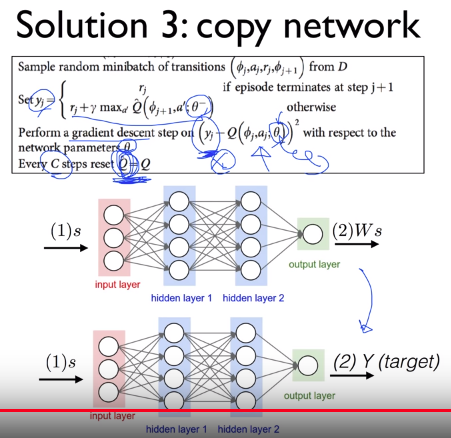You copy parameters from first network into second network # In formular in box, # $$$r_{j}+\gamma max_{a'} \hat{Q}(\phi_{j+1},a';\bar{\theta})$$$ is target $$$y_{j}$$$, # you will create target from $$$\bar{\theta}$$$ # You will create prediction from another network using $$$\theta$$$ # $$$Q(\phi_{j},a_{j};\theta)$$$ # And you will perform gradient descent in respect to $$$\theta$$$, # which means you update only second main network, # without touching target network $$$y_{j}$$$ having $$$\bar{\theta}$$$ # And then, after enough time, you copy Q into $$$\hat{Q}$$$ # img 2018-04-29 12-53-19.png # # @ # Understanding Nature Thesis Paper(2015) about DQN # 1. You create replay memory buffer named D # 1. You create Q main network and $$$\bar{Q}$$$ target network # At initial time, you make those two network same, $$$\bar{\theta}=\theta$$$ # 1. You select action, # you can select action randomly or by using Q network # You execute "action", # You get values like reward, state, # And then, don't train network but copy values into buffer D # ... # img 2018-04-29 12-59-03.png #